Programming Fundamentals

• This page contains extra challenge exercises for week 09.
• These exercises are not compulsory, nor do they provide any marks in the course.
• These exercises are intended for students that want more challenge in the course.
• You cannot submit any of these exercises, however autotests are available for them (Command included at bottom of each exercise).

Download list_delete_range.c here

Or, copy these file(s) to your CSE account using the following command:

1511 fetch-activity list_delete_range

Your task is to add code to this function in list_delete_range.c:

//
// Given the head of a linked list, deletes all nodes in range `start` to `end`.
// Nodes can be identified by an "index", of which the first node has index 0.
//
// Returns the head of the list afterwards.
//
struct node *delete_range(struct node *head, int start, int end) {
    // TODO: COMPLETE THIS FUNCTION AND CHANGE THIS RETURN
    return NULL;
}

In this exercise, every node in the linked list provided can be thought of as having a "place" in the list. For example, the first node will be at place "1", the second at place "2" and so on. You will be given both a start/end position in which all nodes inbetween (inclusive) are to be deleted.

Examples

dcc list_delete_range.c -o list_delete_range
./list_delete_range
Total numbers: 6
6 5 4 3 2 1
Enter delete range: 2 4
List before: [6, 5, 4, 3, 2, 1]
List after: [6, 5, 1]
./list_delete_range
Total numbers: 10
5 1 10 -1 3 6 -5 3 40 1
Enter delete range: 3 8
List before: [5, 1, 10, -1, 3, 6, -5, 3, 40, 1]
List after: [5, 1, 10, 1]
./list_delete_range
Total numbers: 5
1 2 3 4 5
Enter delete range: 0 2
List before: [1, 2, 3, 4, 5]
List after: [4, 5]
./list_delete_range
Total numbers: 5
1 2 3 4 5
Enter delete range: 0 10
List before: [1, 2, 3, 4, 5]
List after: []

Assumptions/Restrictions/Clarifications

• You will always be given integer inputs
• When considering the each node in the range, their positioning starts at 0
• The range components will always be given such that start < end
• All range components will be non-negative
• The "end" given can be larger than the length of the list
• The entire delete range can be outside of the list. E.g. if a list has 3 nodes, the delete range can still be 10 to 15.

Recursion

Warning: This challenge is very hard. The provided solution uses a technique called recursion, that is covered early in COMP2521. Students looking for a challenge have lots to gain from completing this challenge. Recursion occurs when a function calls itself in order to solve smaller sub problems of an overall problem, until it reaches a base case that does not require recursion to calculate.

Below is an example program that finds the Nth fibonacci number using recursion. If you are unfamiliar with the Fibonacci sequence please see here

#include 

int fib(int n) {
    if (n == 0 || n == 1) {
        // Base case
        return n;
    }

    // Recursive case
    return fib(n - 1) + fib(n - 2);
}

int main (void) {
    int n = 0;

    scanf("%d", &n);

    printf("The %d(th|nd|st) Fibonacci number is %d\n", n, fib(n));

    return 0;
}

If we consider the case where n = 4, we can build out what is called a recursion tree.

In this tree, the numbers on the edges signify the order in which the functions are called. These functions are resolved in reverse order, returning the their base values (0 or 1) back up to the functions that called them, until fib(4) is resolve to equal 3.

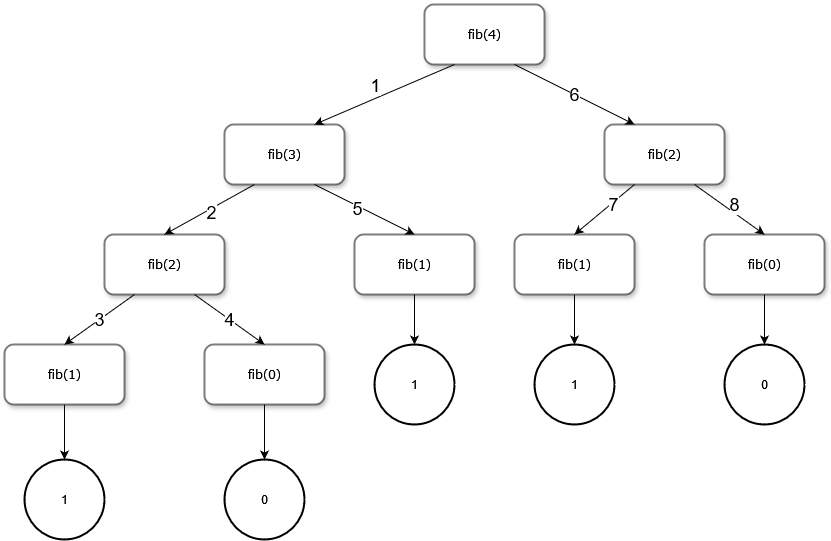
Another representation of this is:

fib(4) = fib(3) + fib(2)
       = (fib(2) + fib(1)) + fib(2)
       = ((fib(1) + fib(0)) + fib(1)) + fib(2)
       = ((fib(1) + fib(0)) + 1) + fib(2)
       = ((1 + 0) + 1) + fib(2)
       = ((1 + 0) + 1) + (fib(1) + fib(0))
       = ((1 + 0) + 1) + (1 + 0)
       = 3

Note: If you do not have a correct/reliable base case, your recursion will continue indefinitely, using up all the memory allocated to the program. This will cause an error called a stack overflow. For more info see here

For the curious student: Another cool use for recursion is to run operations on linked lists. Just beware of causing a stack overflow when your linked list is too big!

Challenge

Write a program that finds attempts to find a solution to a Sudoku puzzle. If there is no solution the program should return "No solution found!".

Examples:

Solution found:

dcc sudoku.c -o sudoku
./sudoku
Enter values: 5 3 0 0 7 0 0 0 0 6 0 0 1 9 5 0 0 0 0 9 8 0 0 0 0 6 0 8 0 0 0 6 0 0 0 3 4 0 0 8 0 3 0 0 1 7 0 0 0 2 0 0 0 6 0 6 0 0 0 0 2 8 0 0 0 0 4 1 9 0 0 5 0 0 0 0 8 0 0 7 9
Solution found!
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9

No solution found:

dcc sudoku.c -o sudoku
./sudoku
Enter values: 0 0 0 0 0 0 0 0 0 0 1 6 0 3 0 0 5 0 0 9 0 0 0 2 0 0 8 0 0 7 0 0 8 0 0 0 0 6 0 0 1 0 3 4 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 4 0 0 2 1 6 7 0 0 5 0 0 4 3 0 0 0
No solution found!

Download list_directions.c here

Or, copy these file(s) to your CSE account using the following command:

1511 fetch-activity list_directions

Your task is to add code to these functions in list_directions.c:

// Given the `head` of a list, prints the string it contains as well as the
// numbers of lefts/rights taken.
void print_list(struct node *head) {
    // TODO: COMPLETE THIS FUNCTION
}

For this exercise, our linked list is setup in a more unique way. Instead of simply having a next pointer, we have a left and right pointer where the list can traverse in either direction. The struct is defined as below:

struct node {
    struct node *left;
    struct node *right;
    char         data;
};

Every node that exists in the linked list has a pointer to the next node through either their left or right pointers. There is only one path through the list, notably, for any node, at least one of the pointers will be NULL, whereas the other pointer will point at the next node.

The program will be provided with the list by specifying both the data to put in the current node as well as the direction to be taken to the next node. Some example input is provided below:

dcc list_directions.c -o list_directions
./list_directions
Enter list: M L y R W L o L r R d L .

List string:   MyWord.
#Lefts Taken:  4
#Rights Taken: 2

In this example, we specify the data of the current node then which direction we want to head in (either 'L' for left or 'R' for right). We can visualise this list with the diagram below.

Creating this list is taken care of in the provided file. Your job is to output the data of the list as a string and identify how many lefts/rights were taken to traverse the list.

Examples

dcc list_directions.c -o list_directions
./list_directions
Enter list: L L o R n L g R e L r R P R a L t R h L W R i L t R h R T R w L i R s R t R s R A R n L d R T R u L r L n R s

List string:   LongerPathWithTwistsAndTurns
#Lefts Taken:  10
#Rights Taken: 17
./list_directions
Enter list: a L b L c L d L e L f L g L h L i L j L k L l L m L n L o L p L q L r L s L t L u L v L w L x L y L z

List string: abcdefghijklmnopqrstuvwxyz
#Lefts Taken:  25
#Rights Taken: 0

Assumptions/Restrictions/Clarifications

• You will always be given letters as character data for each node
• Each node can only point to 1 other node. That is, either the left/right must be NULL
• Try to separate the problem into two conditions. What do you need to do to traverse left, what do you need to do to traverse right?