Programming Fundamentals
Information
- This page contains extra challenge exercises for week 09.
- These exercises are not compulsory, nor do they provide any marks in the course.
- These exercises are intended for students that want more challenge in the course.
- You cannot submit any of these exercises, however autotests are available for them (Command included at bottom of each exercise).
Exercise
(●●◌)
:
List Delete Range
Download list_delete_range.c here
Or, copy these file(s) to your CSE account using the following command:
1511 fetch-activity list_delete_range
Your task is to add code to this function in list_delete_range.c:
//
// Given the head of a linked list, deletes all nodes in range `start` to `end`.
// Nodes can be identified by an "index", of which the first node has index 0.
//
// Returns the head of the list afterwards.
//
struct node *delete_range(struct node *head, int start, int end) {
// TODO: COMPLETE THIS FUNCTION AND CHANGE THIS RETURN
return NULL;
}
In this exercise, every node in the linked list provided can be thought of as having a "place" in the list. For example, the first node will be at place "1", the second at place "2" and so on. You will be given both a start/end position in which all nodes inbetween (inclusive) are to be deleted.
Examples
dcc list_delete_range.c -o list_delete_range ./list_delete_range Total numbers: 6 6 5 4 3 2 1 Enter delete range: 2 4 List before: [6, 5, 4, 3, 2, 1] List after: [6, 5, 1] ./list_delete_range Total numbers: 10 5 1 10 -1 3 6 -5 3 40 1 Enter delete range: 3 8 List before: [5, 1, 10, -1, 3, 6, -5, 3, 40, 1] List after: [5, 1, 10, 1] ./list_delete_range Total numbers: 5 1 2 3 4 5 Enter delete range: 0 2 List before: [1, 2, 3, 4, 5] List after: [4, 5] ./list_delete_range Total numbers: 5 1 2 3 4 5 Enter delete range: 0 10 List before: [1, 2, 3, 4, 5] List after: []
Assumptions/Restrictions/Clarifications
- You will always be given integer inputs
- When considering the each node in the range, their positioning starts at 0
- The range components will always be given such that
start < end - All range components will be non-negative
- The "end" given can be larger than the length of the list
- The entire delete range can be outside of the list. E.g. if a list has 3 nodes, the delete range can still be 10 to 15.
list_delete_range.c
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#define FALSE 0
#define TRUE 1
#define MAX_LIST_LEN 100
struct node {
struct node *next;
int data;
};
struct node *delete_range(struct node *head, int start, int end);
struct node *array_to_list(int len, int array[]);
void print_list(struct node *head);
void free_list(struct node *head);
// DO NOT CHANGE THIS MAIN FUNCTION
int main(void) {
// get list size
int list_size;
printf("Total numbers: ");
scanf(" %d", &list_size);
// read in numbers
int list[MAX_LIST_LEN] = {0};
int index_count = 0;
while (index_count < list_size && scanf(" %d", &list[index_count])) {
index_count++;
}
if (index_count < list_size) {
printf("You must enter numbers equal to the total provided.\n");
return 1;
}
// create linked list from input numbers
struct node *head = NULL;
if (index_count > 0) {
// list has elements
head = array_to_list(list_size, list);
}
int range_start;
int range_end;
printf("Enter delete range: ");
if (scanf("%d %d", &range_start, &range_end) != 2) {
printf("You must enter both a start and an end for the range.\n");
return 2;
}
printf("List before: ");
print_list(head);
struct node *new_head = delete_range(head, range_start, range_end);
printf("List after: ");
print_list(new_head);
free_list(new_head);
return 0;
}
//
// Given the head of a linked list, deletes all nodes in range `start` to `end`.
// Nodes can be identified by an "index", of which the first node has index 0.
//
// Returns the head of the list afterwards.
//
struct node *delete_range(struct node *head, int start, int end) {
// `start` should always be less than `end` in a range.
if (start > end) {
return head;
}
// Keep track of the nodes before and after deletion range.
struct node *before_range = NULL;
struct node *after_range = NULL;
// Flag for whether we are currently in the deletion range
int in_deletion_range = FALSE;
int node_count = 0;
struct node *previous = NULL;
struct node *current = head;
while (current != NULL) {
if (node_count == start) {
before_range = previous;
in_deletion_range = TRUE;
}
if (node_count == end + 1) {
after_range = current;
in_deletion_range = FALSE;
}
previous = current;
current = current->next;
if (in_deletion_range == TRUE) {
// Update the head if it were to be deleted, for ease of use later.
if (previous == head) {
head = NULL;
}
free(previous);
}
node_count++;
}
// In this case, we either never entered the range or the entire list was
// in the range.
if (before_range == NULL && after_range == NULL) {
return head;
}
// This indicates that the head was in range and thus removed. As a result,
// `after_range` is the new head.
if (before_range == NULL) {
return after_range;
// Otherwise, we link up the two nodes at the boundaries to get our new
// list.
} else {
before_range->next = after_range;
return head;
}
}
// DO NOT CHANGE THIS FUNCTION
// create linked list from array of ints
struct node *array_to_list(int len, int array[]) {
struct node *head = NULL;
int i = len - 1;
while (i >= 0) {
struct node *n = malloc(sizeof(struct node));
assert(n != NULL);
n->next = head;
n->data = array[i];
head = n;
i--;
}
return head;
}
// DO NOT CHANGE THIS FUNCTION
// print linked list
void print_list(struct node *head) {
printf("[");
for (struct node *n = head; n != NULL; n = n->next) {
// If you're getting an error here,
// you have returned an invalid list
printf("%d", n->data);
if (n->next != NULL) {
printf(", ");
}
}
printf("]\n");
}
// DO NOT CHANGE THIS FUNCTION
// free linked list
void free_list(struct node *head) {
if (head != NULL) {
free_list(head->next);
free(head);
}
}
Exercise
(●●●)
:
Sudoku
Recursion
Warning: This challenge is very hard. The provided solution uses a technique called recursion, that is covered early in COMP2521. Students looking for a challenge have lots to gain from completing this challenge. Recursion occurs when a function calls itself in order to solve smaller sub problems of an overall problem, until it reaches a base case that does not require recursion to calculate.
Below is an example program that finds the Nth fibonacci number using recursion. If you are unfamiliar with the Fibonacci sequence please see here
#includeint fib(int n) { if (n == 0 || n == 1) { // Base case return n; } // Recursive case return fib(n - 1) + fib(n - 2); } int main (void) { int n = 0; scanf("%d", &n); printf("The %d(th|nd|st) Fibonacci number is %d\n", n, fib(n)); return 0; }
If we consider the case where n = 4, we can build out what is called a recursion tree.
In this tree, the numbers on the edges signify the order in which the functions are called. These functions are resolved in reverse order, returning the their base values (0 or 1) back up to the functions that called them, until fib(4) is resolve to equal 3.
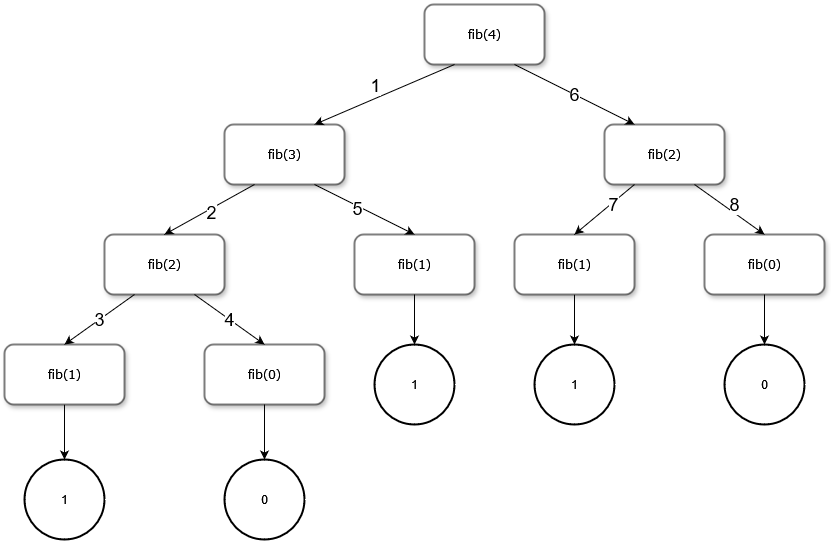
Another representation of this is:
fib(4) = fib(3) + fib(2)
= (fib(2) + fib(1)) + fib(2)
= ((fib(1) + fib(0)) + fib(1)) + fib(2)
= ((fib(1) + fib(0)) + 1) + fib(2)
= ((1 + 0) + 1) + fib(2)
= ((1 + 0) + 1) + (fib(1) + fib(0))
= ((1 + 0) + 1) + (1 + 0)
= 3
Note: If you do not have a correct/reliable base case, your recursion will continue indefinitely, using up all the memory allocated to the program. This will cause an error called a stack overflow. For more info see here
For the curious student: Another cool use for recursion is to run operations on linked lists. Just beware of causing a stack overflow when your linked list is too big!
Challenge
Write a program that finds attempts to find a solution to a Sudoku puzzle. If there is no solution the program should return "No solution found!".
Examples:
Solution found:
dcc sudoku.c -o sudoku ./sudoku Enter values: 5 3 0 0 7 0 0 0 0 6 0 0 1 9 5 0 0 0 0 9 8 0 0 0 0 6 0 8 0 0 0 6 0 0 0 3 4 0 0 8 0 3 0 0 1 7 0 0 0 2 0 0 0 6 0 6 0 0 0 0 2 8 0 0 0 0 4 1 9 0 0 5 0 0 0 0 8 0 0 7 9 Solution found! 5 3 4 6 7 8 9 1 2 6 7 2 1 9 5 3 4 8 1 9 8 3 4 2 5 6 7 8 5 9 7 6 1 4 2 3 4 2 6 8 5 3 7 9 1 7 1 3 9 2 4 8 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 5 2 8 6 1 7 9
No solution found:
dcc sudoku.c -o sudoku ./sudoku Enter values: 0 0 0 0 0 0 0 0 0 0 1 6 0 3 0 0 5 0 0 9 0 0 0 2 0 0 8 0 0 7 0 0 8 0 0 0 0 6 0 0 1 0 3 4 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 4 0 0 2 1 6 7 0 0 5 0 0 4 3 0 0 0 No solution found!
sudoku.c
// Program that solves a sudoku puzzle using recursive backtracking
// Date: 2024 (z5363683@unsw.edu.au)
/*
This solution uses recursion, which occurs when a function calls itself in
order to solve smaller sub problems of an overall problem, until it reaches
a base case that does not require recursion to calculate.
*/
#include <stdio.h>
#include <assert.h>
#define N 9
#define VALID 1
#define INVALID 0
#define SOLVED 1
#define UNSOLVED 0
void print_grid(int grid[N][N]);
int is_valid(int grid[N][N], int row, int col, int num);
int solve_sudoku(int grid[N][N]);
int main(void) {
// DO NOT CHANGE BELOW HERE
int grid[N][N];
// Scan in values for the grid.
printf("Enter values: ");
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
assert(scanf("%d", &grid[i][j]) == 1);
}
}
// DO NOT CHANGE ABOVE HERE
/**
* You may insert code below as you require
*/
if (solve_sudoku(grid)) {
printf("Solution found!\n");
print_grid(grid);
}
else {
printf("No solution found!\n");
}
return 0;
}
/**
* Function that prints the grid.
*
* DO NOT CHANGE THIS FUNCTION
*/
void print_grid(int grid[N][N]) {
// DO NOT CHANGE THIS FUNCTION
for (int row = 0; row < N; row++) {
for (int col = 0; col < N; col++) {
printf("%d ", grid[row][col]);
}
printf("\n");
}
// DO NOT CHANGE THIS FUNCTION
}
/**
* Returns 0 when invalid
* Returns 1 when valid
*
* There are three conditions required for a number to be valid.
* - The number must not be present in the row
* - The number must not be present in the column
* - The number must not be present in the 3x3 sub-grid
* */
int is_valid(int grid[N][N], int row, int col, int num) {
// Check if the number is already in the row
for (int j = 0; j < N; j++) {
if (grid[row][j] == num) {
return INVALID;
}
}
// Check if the number is already in the column
for (int i = 0; i < N; i++) {
if (grid[i][col] == num) {
return INVALID;
}
}
// Check if the number is already in the 3x3 sub-grid
int row_start = row - row % 3;
int col_start = col - col % 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (grid[i + row_start][j + col_start] == num) {
return INVALID;
}
}
}
return VALID;
}
/**
* Returns 0 when a solution is found
* Returns 1 when no solution was found
*
* This function uses recursion to search for valid numbers.
* If a valid number isn't found, it backtracks, resetting numbers and searching for
* a different valid number.
* If there are no empty cells, then the grid is full and the game has been solved.
* Otherwise, if the recursion cannot find a valid combination, the function will return
*/
int solve_sudoku(int grid[N][N]) {
int row, col;
// Loop over the grid, searching for an empty cell
int found = 0;
for (row = 0; row < N; row++) {
for (col = 0; col < N; col++) {
if (grid[row][col] == 0) {
found = 1;
break;
}
}
if (found) {
break;
}
}
// If no empty cell is found, we have solved sudoku!!
if (!found) {
return SOLVED;
}
// Try placing numbers from 1 to 9 in the empty cell
for (int num = 1; num <= 9; num++) {
// This loop will only be entered if we have found a cell with no number.
// This prevents the backtracking from removing a cell from the base grid.
if (is_valid(grid, row, col, num)) {
grid[row][col] = num;
if (solve_sudoku(grid)) {
return SOLVED;
}
grid[row][col] = 0; // If the solution is not found, backtrack
}
}
return UNSOLVED;
}
Exercise
(●●●)
:
List Directions
Download list_directions.c here
Or, copy these file(s) to your CSE account using the following command:
1511 fetch-activity list_directions
Your task is to add code to these functions in list_directions.c:
// Given the `head` of a list, prints the string it contains as well as the
// numbers of lefts/rights taken.
void print_list(struct node *head) {
// TODO: COMPLETE THIS FUNCTION
}
For this exercise, our linked list is setup in a more unique way. Instead of
simply having a next pointer, we have a left and right pointer where the
list can traverse in either direction. The struct is defined as below:
struct node {
struct node *left;
struct node *right;
char data;
};
Every node that exists in the linked list has a pointer to the next node
through either their left or right pointers. There is only one path through
the list, notably, for any node, at least one of the pointers will be NULL,
whereas the other pointer will point at the next node.
The program will be provided with the list by specifying both the data to put in the current node as well as the direction to be taken to the next node. Some example input is provided below:
dcc list_directions.c -o list_directions ./list_directions Enter list: M L y R W L o L r R d L . List string: MyWord. #Lefts Taken: 4 #Rights Taken: 2
In this example, we specify the data of the current node then which direction we want to head in (either 'L' for left or 'R' for right). We can visualise this list with the diagram below.
Creating this list is taken care of in the provided file. Your job is to output the data of the list as a string and identify how many lefts/rights were taken to traverse the list.
Examples
dcc list_directions.c -o list_directions ./list_directions Enter list: L L o R n L g R e L r R P R a L t R h L W R i L t R h R T R w L i R s R t R s R A R n L d R T R u L r L n R s List string: LongerPathWithTwistsAndTurns #Lefts Taken: 10 #Rights Taken: 17 ./list_directions Enter list: a L b L c L d L e L f L g L h L i L j L k L l L m L n L o L p L q L r L s L t L u L v L w L x L y L z List string: abcdefghijklmnopqrstuvwxyz #Lefts Taken: 25 #Rights Taken: 0
Assumptions/Restrictions/Clarifications
- You will always be given letters as character data for each node
- Each node can only point to 1 other node. That is, either the left/right must
be
NULL - Try to separate the problem into two conditions. What do you need to do to traverse left, what do you need to do to traverse right?
list_directions.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
struct node {
struct node *left;
struct node *right;
char data;
};
void print_list(struct node *head);
struct node *scan_in_list();
// DO NOT CHANGE THIS MAIN FUNCTION
int main(void) {
printf("Enter list: ");
struct node *head = scan_in_list();
print_list(head);
return 0;
}
// Given the `head` of a list, prints the string it contains as well as the
// numbers of lefts/rights taken.
void print_list(struct node *head) {
struct node *current = head;
int left_count = 0;
int right_count = 0;
printf("List string: ");
while (current != NULL) {
printf("%c", current->data);
// Traverse either left or right based on where the next node would be.
// Since left/right counts need to be accounted for, both the left and
// right pointers need to be checked more explicitly.
if (current->left == NULL && current->right == NULL) {
current = NULL;
} else if (current->left == NULL) {
current = current->right;
right_count++;
} else {
current = current->left;
left_count++;
}
}
printf("\n");
printf("#Lefts Taken: %d\n", left_count);
printf("#Rights Taken: %d\n", right_count);
}
// Malloc's a new node given `left`, `right`, `data` values. Returns this node.
struct node *create_node(struct node *left, struct node *right, char data) {
struct node *new = malloc(sizeof(struct node));
new->left = left;
new->right = right;
new->data = data;
return new;
}
// DO NOT CHANGE THIS FUNCTION
// Handles input/output to scan in a list
struct node *scan_in_list() {
char data;
char direction;
// Head of list is NULL if no initial data is given.
if (scanf(" %c", &data) != 1) {
return NULL;
}
struct node *head = create_node(NULL, NULL, data);
struct node *previous_node = head;
// Loop through for every (direction, data) pair and linked up list
while (scanf(" %c %c", &direction, &data) == 2) {
assert(direction == 'L' || direction == 'R');
struct node *new = create_node(NULL, NULL, data);
if (direction == 'L') {
previous_node->left = new;
previous_node = previous_node->left;
} else {
previous_node->right = new;
previous_node = previous_node->right;
}
}
return head;
}