Week 04 Tutorial Questions
Graph Algorithms, Sorting
Graph Algorithms
-
In the following graph:

- Which vertices are reachable from vertex 0?
- Which vertices are reachable from vertex 1?
- Which vertices are reachable from vertex 5?
- Which vertices are reachable from vertex 6?
-
Write a C function that takes a Graph and a starting Vertex and returns a set containing all of the vertices that can be reached by following a path from the starting point. Use the function template:
Set reachable(Graph g, Vertex src) { ... }
You may use any of the standard ADTs from the slides (e.g. Sets, Lists, Stacks, Queues).
-
Trace the execution of Dijkstra's algorithm on the following graph to compute the minimum distances from source node 0 to all other vertices:
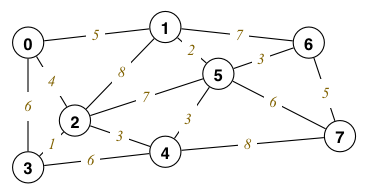
Show the values of vSet, dist[] and pred[] after each iteration.
A helpful resource you can use to check your answer and visualise Dijkstra's algorithm (as well as BFS and DFS) is Graph visualiser by Jonah.
-
Kruskal's algorithm for finding a minimum spanning tree of a graph can be expressed as follows:
typedef Graph MSTree; MSTree kruskalFindMST(Graph g) { MSTree mst = GraphNew(g->nV); // MST initially empty Edge eList[g->nE]; // sorted array of edges edges(eList, g->nE, g); sortEdgeList(eList, g->nE); for (int i = 0; mst->nE < g->nV - 1; i++) { Edge e = eList[i]; GraphAddEdge(mst, e); if (GraphHasCycle(mst)) GraphRemoveEdge(mst, e); } return mst; }
This algorithm effectively constructs the MST by gradually joining together the connected graphs in a forest that starts with each subgraph being a single node. On each iteration, it add a new edge to the forest, and reduces the number of subgraphs by one. Show how it would construct the MST for the graph below:
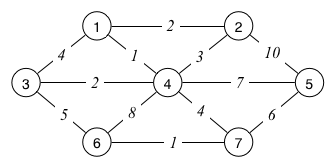
How many edges did we have to consider? For a graph \( G(V, E) \), what is the least number of edges we might need to consider? What is the most number of edges we might have to consider? Add another edge to the above graph to force Kruskal's algorithm to the worst case.
-
Prim's algorithm for finding a MST of a graph can be expressed abstractly as follows:
- Start from any vertex v and empty MST
- Choose edge not already in MST, satisfying
- incident on a vertex s already in MST
- incident on a vertex t not already in MST
- with minimal weight of all such edges
- Add chosen edge to MST
- Repeat until MST covers all vertices
Show how Prim's algorithm produces an MST on the following graph:
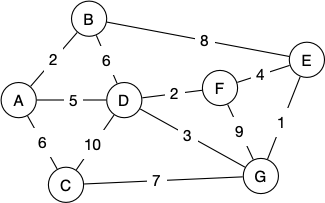
Start at vertex A.
Sorting Algorithms
Resources
-
Consider the following simple table of enrolments, sorted by course code:
course name program COMP1927 Jane 3970 COMP1927 John 3978 COMP1927 Pete 3978 MATH1231 John 3978 MATH1231 Adam 3970 PSYC1011 Adam 3970 PSYC1011 Jane 3970 Now we wish to sort it by student name, so that we can easily see what courses each student is studying. Show an example of what the final array would look like if
- we used a stable sorting algorithm
- we used an unstable sorting algorithm
-
Compare the performance of bubble sort and insertion sort on the following types of input:
- Sorted (e.g., \([1, 2, 3, \ldots, n]\))
- Reverse-sorted (e.g., \([n, n - 1, n - 2, \ldots, 1]\))
- Sorted, except the first and last numbers are swapped (e.g., \([n, 2, 3, \ldots, n - 1, 1]\))
-
Merge sort is typically implemented as follows:
void mergeSort(int A[], int lo, int hi) { if (lo >= hi) return; int mid = (lo + hi) / 2; mergeSort(A, lo, mid); mergeSort(A, mid + 1, hi); merge(A, lo, mid, hi); } void merge(int A[], int lo, int mid, int hi) { int nitems = hi - lo + 1; int *tmp = malloc(nitems * sizeof(int)); int i = lo; int j = mid + 1; int k = 0; // scan both segments into tmp while (i <= mid && j <= hi) { if (A[i] <= A[j]) { tmp[k++] = A[i++]; } else { tmp[k++] = A[j++]; } } // copy items from unfinished segment while (i <= mid) tmp[k++] = A[i++]; while (j <= hi) tmp[k++] = A[j++]; // copy items from tmp back to main array for (i = lo, k = 0; i <= hi; i++, k++) { A[i] = tmp[k]; } free(tmp); }
Suppose that at a particular point during the execution of the
mergeSortfunction, the arrayAlooks like this:{ 1, 4, 5, 6, 7, 2, 3, 4, 7, 9 }
Show how the call
merge(A, 0, 4, 9)would merge the elements of the two sorted subarrays into a single sorted array. -
An important operation in the quicksort algorithm is partition, which takes an element called the pivot, and reorganises the elements in the subarray
A[lo..hi]such that all elements to the left of the pivot in the subarray are less than or equal to the pivot, and all elements to the right of the pivot in the subarray are greater than the pivot.Here is one possible implementation of partition:
int partition(int A[], int lo, int hi) { int pivot = A[lo]; int l = lo + 1; int r = hi; while (true) { while (l < r && A[l] <= pivot) l++; while (l < r && A[r] >= pivot) r--; if (l == r) break; swap(A, l, r); } if (pivot < A[l]) l--; swap(A, lo, l); return l; }
Show how the call
partition(A, 0, 9)would partition each of these arrays. What index is returned by each of these calls?{ 5, 3, 9, 6, 4, 2, 9, 8, 1, 7 }{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }{ 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }
-
Consider the following shell sort algorithm (based on Sedgewick's implementation):
void shellSort(int a[], int lo, int hi) { int h; for (h = 1; h <= (hi - lo) / 9; h = 3 * h + 1); for (; h > 0; h /= 3) { for (int i = lo + h; i <= hi; i++) { int val = a[i]; int j = i; while (j >= lo + h && val < a[j - h]) { a[j] = a[j - h]; j -= h; } a[j] = val; } } }
Describe how this would sort an array containing the first 100 positive integers sorted in descending order (i.e.
{100, 99, 98, 97, 96, 95, ... , 1}).