Week 03 Tutorial Questions

Balanced Trees, Graph Basics

Balancing Trees

  1. Show how the following tree would change if we do a right rotation on the node containing 10 followed by a left rotation on the node containing 6.

  2. Show the result of performing the insert-at-root operation with the value 7 in this binary search tree:

AVL Trees

AVL trees use the following node definition:

struct node {
    int data;
    int height;
    struct node *left;
    struct node *right;
};

You may find these resources on AVL trees useful:

  1. For the following AVL tree, annotate each node with the height of its subtree.

    Now starting from the initial tree each time, insert the following integers:

    0  2  10  17

  2. Show how an AVL tree would be constructed if the following values were inserted into an initially empty tree in the order given:

    12  10  8  6  4  2

  3. Using an AVL tree, design an algorithm to determine if an array contains two elements that sum to a given value.

    1. Write the algorithm in pseudocode.
    2. Analyse the time complexity of your algorithm.
Graph Representation

  1. Consider the following graph

    The edges are labelled simply for convenience in describing graph properties.

    1. How many edges does it have?
    2. How many cycles are there in the graph?
    3. How many cliques are there in the graph?
    4. What is the degree of each vertex?
    5. How many edges in the longest path from 5 to 8?
      (without traversing any edge more than once)

  2. For each of the following graphs:

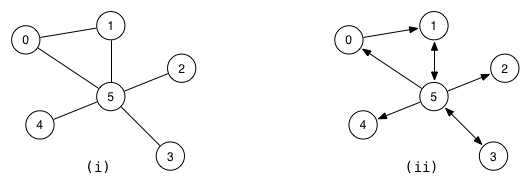
    Show the concrete data structures if the graph was implemented via:

    1. adjacency matrix representation (assume a full \( V \times V \) matrix)
    2. adjacency list representation (if non-directional, include both \( (v, w) \) and \( (w, v) \))

  3. How is the adjacency matrix for a directed graph different to that for an undirected graph?

  4. Facebook could be considered as a giant "social graph"

    1. What are the vertices?
    2. What are the edges?
    3. Are edges directional?
    4. What does the degree of each vertex represent?
    5. What kind of graph algorithm could suggest potential friends?
Graph Traversal

  1. Consider the breadth-first and depth-first traversal algorithms below and the following graph:

    void breadthFirst(Graph g, int src) {
	bool *visited = calloc(g->nV, sizeof(bool));
	int *pred = calloc(g->nV, sizeof(int));
	Queue q = QueueNew();

	visited[src] = true;
	QueueEnqueue(q, src);
	while (!QueueIsEmpty(q)) {
		int v = QueueDequeue(q);


		printf("%d\n", v);
		for (int w = 0; w < g->nV; w++) {
			if (g->edges[v][w] && !visited[w]) {
				visited[w] = true;
				pred[w] = v;
				QueueEnqueue(q, w);
			}
		}
	}

	free(visited);
	free(pred);
	QueueFree(q);
}

    void depthFirst(Graph g, int src) {
	bool *visited = calloc(g->nV, sizeof(bool));
	int *pred = calloc(g->nV, sizeof(int));
	Stack s = StackNew();

	StackPush(s, src);
	while (!StackIsEmpty(s)) {
		int v = StackPop(s);

		if (visited[v]) continue;
		visited[v] = true;

		printf("%d\n", v);
		for (int w = g->nV - 1; w >= 0; w--) {
			if (g->edges[v][w] && !visited[w]) {
				pred[w] = v;
				StackPush(s, w);
			}
		}
	}

	free(visited);
	free(pred);
	StackFree(s);
}

    Trace the execution of the traversal algorithms, and show the state of the visited and pred arrays and the Queue (BFS) or Stack (DFS) at the end of each iteration, for each of the following function calls:

    breadthFirst(g, 0);
breadthFirst(g, 3);
depthFirst(g, 0);
depthFirst(g, 3);