Q2 (15 marks)

Design a solution to compute all k-cores in large graphs.

Problem Statement:

In this question, you need to design a solution to query all k-cores given an arbitrary integer k in a large undirected unweighted graph.

Background & Marking Criteria

The details about k-core can be found in Topic 3.1. Given the integer k, there may exist multiple k-cores in the graph. You are expected to preprocess the graph and build an index structure to speed up computing all k-cores with a given k. You can preprocess the graph data in any way you like. The output should be the vertices for each k-core. For example, consider the graph in Figure 1 and k = 3. There are two 3-cores. The query output should be [[v₁, v₂, v₃, v₄],[v₆, v₇, v₈, v₉]]. Note that you are allowed to output the result in a different order. That means [[v₇,v₆,v₈, v₉],[v₁, v₃, v₄, v₂]] is also a valid output.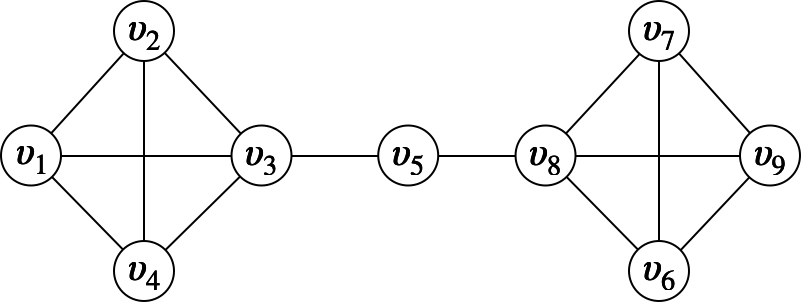

The marking tutors will evaluate the goodness of your solution. A good solution should consider query processing time, index space, and index construction time. In addition to writing out the code, it is also important to understand what you have achieved. You need to provide a document to describe your solution. The document helps us understand your code, and let us know you have already got an idea to solve the problem at least, which may provide you some marks even if your code cannot run correctly. The document can be in any format. The content should include but not limited to your designing ideas, theoretical analysis for space and time complexity. Example figures (e.g., index structure) will be helpful if you design some complex solutions. You are also welcome to discuss multiple potential solutions/baselines and demonstrate why your solution is the best.

Doing this Project

Open the code template file Q2.ipynb and make a copy of the file in your own google drive. You need to implement a function named KCore. Below is the code template for KCore shown in Q2.ipynb.

  
    ################################################################################
    # You can import any Python Standard Library modules~
    import networkx as nx
    ################################################################################
    
    class KCore(object):
        def __init__(self, G):
            ################################################################################
            # TODO: You may add some index data structures here~
            # analyze the space usage/complexity of the index (all additional data structures)~
            ################################################################################
            self.preprocess(G)
    
        def preprocess(self, G):
            ################################################################################
            # TODO: Your code here~
            # precompute some index data structures for G and use them to speed up query processing
            # analyze the time complexity of preprocess()
            ################################################################################
            return
    
        def query(self, k):
            cores = [[]]
            ################################################################################
            # TODO: Your code here~
            # Input: k
            # Output: the k-cores
            # analyze the time complexity of query()
            ################################################################################
            return cores
    
        ################################################################################
        # You can define any auxiliary functions~
        ################################################################################

You can also find the input graph data stucture defined in the UndirectedUnweightedGraph class and an example about how we test your code. The file is running on the Google Colab plarform, which has already integrated the Python environment. As shown in our tutorials, you can directly write and run your code without any configuration. You can directly add any description for your solution and theoretical analysis in your your Q2.ipynb instead of creating a seperated PDF report. Ask your tutor if you have any difficult to run the code.

Marking Criteria

Only correctly implementing the ComputeCore (online solution) in Topic 3.2 with O(m+n) time complexity and returning the correct output is worth at most 4 points.
Any reasonable algorithm is acceptable as long as you provide a detailed description and analysis in the report. The mark is provided on a case-by-case basis. Usually, a reasonable and correct index-based solution is worth at least 6 points.

Notes:

A detailed report is required to describe your algorithm, which at least analyses the time complexity of query processing and index construction, and the space complexity of the index. You can directly write them in Q2.ipynb or in a separated Q2.pdf.
Any reasonable algorithm is acceptable as long as you have a detailed description and analysis in the report.
You can add additional variables and functions for KCore. Do not change the input/output format in the code template.
We may use a different and much larger dataset to test your algorithm.