Extra Lab Exercise
Weighted Graphs and Geo Data
Objectives
- To implement a variant of path finding in a weighted graph
- To see how graphs might be used with real-world data
Admin
This lab is not marked and there is no submission for it.
Background
Geographic data is widely available, thanks to sites such as GeoNames. For this lab, we have downloaded data files from the City Distance Dataset by John Burkardt from the Department of Scientific Computing at Florida State University. The dataset that we will use contains information about distances between 30 prominent cities/locations around the world. These are great-circle distances; we'll assume that these are the distances that an aircraft would fly between two cities. The data that we have forms a complete graph in that there is a distance recorded for every pair of cities.
The following diagram shows a subset of the data from the City Distance Dataset.
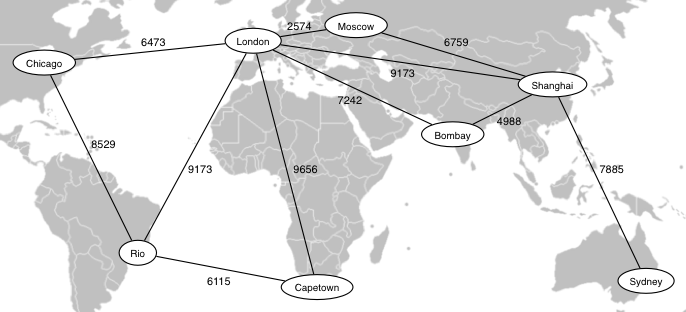
Own work. Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons
The data comes in two files:
ha30_dist.txtThis file contains a matrix of distances between cities. This is essentially the adjacency matrix for a weighted graph where the vertices are cities and the edge weights correspond to distances between cities. As you would expect for an adjacency matrix, the leading diagonal contains all zeroes (in this case, corresponding to the fact that a city has a distance of zero from itself).
ha30_name.txtThis file contains one city name per line. If we number the lines starting from zero, then the line number corresponds to the vertex number for the city on that line. For example, the Azores is on line 0, so vertex 0 corresponds to the Azores, and the first line in the distance file gives distances from the Azores to the other 29 cities. The last line (line 29) tells us that Tokyo is vertex 29, and the last line in the distance files gives distances between Tokyo and all other cities.
Setting Up
Set up a directory for this lab, change into that directory, and run the following command:
unzip /web/cs2521/24T3/labs/week16/downloads/files.zip
If you're working at home, download files.zip by clicking on the above link and then run the unzip command on the downloaded file.
If you've done the above correctly, you should now have the following files:
Makefile- a set of dependencies used to control compilation
travel.c- main program to load and manipulate the graph
Graph.h- the interface for the Graph ADT
Graph.c- an incomplete implementation of the Graph ADT
Queue.h- the interface for the Queue ADT
Queue.c- a complete implementation of the Queue ADT
ha30_name.txt- the city name file described above
ha30_dist.txt- the distance matrix file described above
The Makefile produces a file called travel based on the main program in travel.c and the functions in Graph.c. The travel program takes either zero or two command line arguments:
./travel ... displays the entire graph ... ... produces lots of output, so either redirect to a file or use less ... ./travel from-city to-city ... display a route to fly between specified cities ...
If given zero arguments, it simply displays the graph. If given two arguments, it treats the first city as a starting point and the second city as a destination, and determines a route between the two cities, based on "hops" between cities with direct flights.
Read the main() function so that you understand how it works, and, in particular, how it invokes the functions that you need to implement.
The Graph ADT in this week's lab has a GraphRep data structure that is a standard adjacency matrix representation of the kind we looked at in lectures. However, some aspects of it are different to the GraphRep from lectures.
Note that city names are not stored as part of the GraphRep data structure. The Graph ADT deals with vertices using their numeric ID. The main program maintains the list of city names and passes this list to the showGraph() function when it is called to display the graph. This means that the calling interface for the showGraph() function is different to the showGraph() function from the Graph ADT in lectures.
Another difference between this Graph ADT and the one used in lectures is that the values stored in the matrix are not simply zero and one, but represent the distances between vertices. In other words, we're dealing with a weighted graph. A weight value of zero indicates that there is no edge between two vertices, while a non-zero weight indicates that there is an edge.
The main program makes some changes to the edges implied by the distance matrix as it copies them into the Graph. The values in the ha30_dist.txt file are given in units of "hundreds of miles"; we want them in units of kilometres so each distance is converted before it is added to the graph as the weight of an edge. Since every city has a distance to every other city (except itself), this gives us a complete graph.
As supplied, Graph.c has an incomplete implementation of the findPath() function. If you compile the travel program and try to find any route, it will simply tell you that there isn't one. Your task will be to implement this function.
Exercise
Implement the findPath(g, src, dest, max, path) function. This function takes a graph g, two vertex numbers src and dest, a maximum flight distance max, and fills the path array with a sequence of vertex numbers giving the "shortest" path from src to dest such that no edge on the path has weight larger than max. The function returns the number of vertices stored in the path array; if it cannot find a path, it returns zero. The path array is assumed to have enough space to hold the longest possible path (which would include all vertices).
This could be solved with a standard BFS graph traversal algorithm, but there are two twists for this application:
The edges in the graph represent real distances, but the user of the
travelprogram (the traveller) isn't necessarily worried about real distances. They are more worried about the number of take-offs and landings (which they find scary), so the length of a path is measured in terms of the number of edges, not the sum of the edge weights. Thus, the "shortest" path is the one with the minimum number of edges.While the traveller isn't concerned about how far a single flight goes, aircrafts are affected by this (because they hold a limited amount of fuel). The
maxparameter forfindPath()allows a user to specify that they only want to consider flights whose length is at mostmaxkilometres (i.e. only edges whose weight is not more thanmax).
Your implementation of findPath() must satisfy both of the above.
In implementing findPath(), you can make use of the Queue ADT that we've supplied.
Note that the default value for max, set in the main function, is 10000km. Making the maximum flight distance smaller produces more interesting paths (see below), but if you make it too small (e.g., 5000km) you will end up isolating Australia from the rest of the world. With a maximum flight distance of 6000km, the only way out of Australia is via Guam. If you make the maximum flight distance large enough (e.g., possibly reflecting an improvement in aircraft technology), every city will be reachable from every other city in a single hop.
Here are some example routes (don't expect them to closely match reality):
# when no max distance is given on the command line, # we assume that planes can fly up to 10000km before refuelling ./travel Berlin Chicago Least-hops route: Berlin -> Chicago ./travel Sydney Chicago Least-hops route: Sydney -> Honolulu -> Chicago ./travel Sydney London Least-hops route: Sydney -> Shanghai -> London ./travel London Sydney Least-hops route: London -> Shanghai -> Sydney ./travel Sydney 'Buenos Aires' Least-hops route: Sydney -> Honolulu -> Chicago -> Buenos Aires # if planes can fly up to 6000km before refuelling ./travel Sydney London 6000 Least-hops route: Sydney -> Guam -> Manila -> Bombay -> Baghdad -> London # if planes can fly up to 5000km before refuelling # you can't leave Australia under this scenario ./travel Sydney 'Buenos Aires' 5000 No route from Sydney to Buenos Aires # if planes can fly up to 7000km before refuelling ./travel Sydney 'Buenos Aires' 7000 Least-hops route: Sydney -> Guam -> Honolulu -> Chicago -> Panama City -> Buenos Aires # if planes can fly up to 8000km before refuelling ./travel Sydney 'Buenos Aires' 8000 Least-hops route: Sydney -> Guam -> Honolulu -> Mexico City -> Buenos Aires # if planes can fly up to 11000km before refuelling ./travel Sydney 'Buenos Aires' 11000 Least-hops route: Sydney -> Bombay -> Azores -> Buenos Aires # if planes can fly up to 12000km before refuelling # we can reach Buenos Aires in a single flight ./travel Sydney 'Buenos Aires' 12000 Least-hops route: Sydney -> Buenos Aires ./travel Bombay Chicago 5000 Least-hops route: Bombay -> Istanbul -> Azores -> Montreal -> Chicago ./travel Sydney Sydney Least-hops route: Sydney
The above routes were generated using an algorithm that checks vertices in numeric order (vertex 0 before vertex 1 before vertex 2, etc.). If you check vertices in a different order, you may generate different, but possibly equally valid, routes.