Week 04 Tutorial Questions

Objectives

introducing the arithmetic needed to manipulate multi-dimensional arrays in MIPS
introducing the concept of program stack frames to allow for function-call operations
introduce the MIPS representation of more complex data structures like custom structs

Often when writing large MIPS programs, you will make accidental errors that cause your program to misbehave.
Discuss what tools are available to help debug broken MIPS code.

Translate this C program to MIPS assembler.

// This program prints out a danish flag, by
// looping through the rows and columns of the flag.
// Each element inside the flag is a single character.
// (i.e., 1 byte).
//
// (Dette program udskriver et dansk flag, ved at
// sløjfe gennem rækker og kolonner i flaget.)
//

#include <stdio.h>

#define FLAG_ROWS 6
#define FLAG_COLS 12

char flag[FLAG_ROWS][FLAG_COLS] = {
    {'#', '#', '#', '#', '#', '.', '.', '#', '#', '#', '#', '#'},
    {'#', '#', '#', '#', '#', '.', '.', '#', '#', '#', '#', '#'},
    {'.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'},
    {'.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'},
    {'#', '#', '#', '#', '#', '.', '.', '#', '#', '#', '#', '#'},
    {'#', '#', '#', '#', '#', '.', '.', '#', '#', '#', '#', '#'}
};

int main(void) {
    for (int row = 0; row < FLAG_ROWS; row++) {
        for (int col = 0; col < FLAG_COLS; col++) {
            printf("%c", flag[row][col]);
        }
        printf("\n");
    }
}

Translate this C program to MIPS assembler.

// C function to find the largest element in an array, recursively.
// Returns the value of the largest element in the array.
// 
// array:  Array to search
// length: Number of elements in the array
int max(int array[], int length) {
    // 
    int first_element = array[0];
    if (length == 1) {
        // Handle the base-case of the recursion, at the end of the array.
        return first_element;
    } else {
        // Recurse on the rest of the array.
        // Finds the largest element after first_element in the array.
        int max_so_far = max(&array[1], length - 1);

        // Compare this element with the largest element after it in the array.
        if (first_element > max_so_far) {
            max_so_far = first_element;
        }
        return max_so_far;
    }
}

Consider the following operation that multiplies all of the elements in a matrix by a constant factor:

This operation could be rendered in C99-standard C as

/**
 * C function to multiply a matrix by a scalar.
 * 
 * nrows:  Number of rows in the matrix
 * ncols:  Number of columns in the matrix
 * M:      Matrix M
 * factor: Scalar factor to multiply by
 */
void change (int nrows, int ncols, int M[nrows][ncols], int factor)
{
    for (int row = 0; row < nrows; row++) {
        for (int col = 0; col < ncols; col++) {
            M[row][col] = factor * M[row][col];
        }
    }
}

Write a function in MIPS assembly equivalent to the above C code. Assume that the arguments are placed in the $a? registers in the order given in the function definition. e.g., the function could be called as follows in MIPS:

   li   $a0, 3
   li   $a1, 4
   la   $a2, M
   li   $a3, 2
   jal  change

Where M is defined as:

    .data
M:  .word 1, 2, 3, 4
    .word 3, 4, 5, 6
    .word 5, 6, 7, 8

Translate this C program to MIPS assembler using normal function calling conventions.

sum2 is a very simple function but don't rely on this when implementing sum4.

// sum 4 numbers using function calls

#include <stdio.h>

int sum4(int a, int b, int c, int d);
int sum2(int x, int y);

int main(void) {
    int result = sum4(11, 13, 17, 19);
    printf("%d\n", result);
    return 0;
}

int sum4(int a, int b, int c, int d) {
    int res1 = sum2(a, b);
    int res2 = sum2(c, d);
    return sum2 (res1, res2);
}

int sum2(int x, int y) {
    return x + y;
}

Consider the following 3-d array structure:

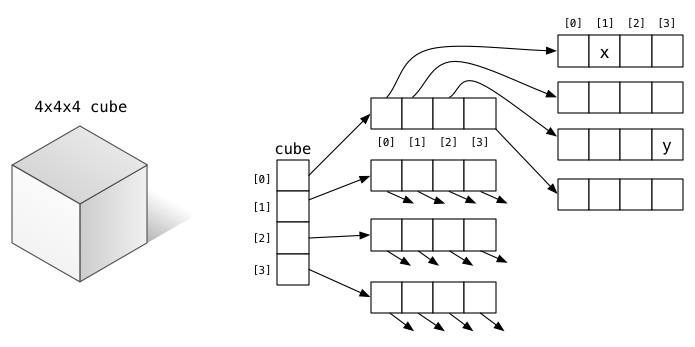
The cube could be implemented as an array of pointers, each of which points to a slice of the cube. Each slice of the cube is also an array of pointers, and each of those points to an array of int values.
For example, in the diagram above, the cell labelled x can be accessed as cube[0][0][1], and the cell labelled y can be accessed as cube[0][2][3].
1. Write MIPS assembler directives to define a data structure like this.
2. Write MIPS assembler code to scan this cube, and count the number of elements which are zero.
In other words, implement the following C code in MIPS.
```
int cube[4][4][4];

int nzeroes = 0;
for (int x = 0; x < 4; x++)
    for (int y = 0; y < 4; y++)
        for (int z = 0; z < 4; z++)
            if (cube[x][y][z] == 0)
                nzeroes++;
```

For each of the following struct definitions, what are the likely offset values for each field, and the total size of the struct:

struct _coord {
    double x;
    double y;
};

typedef struct _node Node;
struct _node {
    int value;
    Node *next;
};

struct _enrolment {
    int stu_id;         // e.g. 5012345
    char course[9]:     // e.g. "COMP1521"
    char term[5];       // e.g. "17s2"
    char grade[3];      // e.g. "HD"
    double mark;        // e.g. 87.3
};

struct _queue {
    int nitems;     // # items currently in queue
    int head;       // index of oldest item added
    int tail;       // index of most recent item added
    int maxitems;   // size of array
    Item *items;    // malloc'd array of Items
};

Both the offsets and sizes should be in units of number of bytes.

Topographic Maps are a common way to represent terrain of various kinds, by providing a representation of the height of the terrain at various points. This C code provides a (heavily simplified) representation of how one might read a topographic map, and so find the height of the terrain at a given point.

// A topographic map!
// This helpful tool will tell explorers how much they need to climb to
// reach various points of interest.
// Given an array of points, `my_points`, it can look up individual cells
// in the 2D map and print their height.

#include <stdio.h>

#define MAP_SIZE 5
#define N_POINTS 4

// 2D representation of a point, stored as a single struct
struct point2D {
    int row;
    int col;
} typedef point2D_t;

// 2D grid representing the height data for an area.
int topography_grid[MAP_SIZE][MAP_SIZE] = {
    {0, 1, 1, 2, 3},
    {1, 1, 2, 3, 4},
    {1, 2, 3, 5, 7},
    {3, 3, 4, 5, 6},
    {3, 4, 5, 6, 7},
};

// Points of interest to print heights for, as a 1D array.
point2D_t my_points[N_POINTS] = {
    {1, 2},
    {2, 3},
    {0, 0},
    {4, 4},
};

int main() {
    // Loop over all elements, and print their data
    for (int i = 0; i < N_POINTS; i++) {
        int row = my_points[i].row;
        int col = my_points[i].col;
        int height = topography_grid[row][col];
        printf("Height at %d,%d=%d\n", row, col, height);
    }
    return 0;
}

When translating structs, it is useful to consider where each value inside the struct will be stored in memory, and how many it will need in total. Hint: sizeof() may help here.

// The point2D_t struct is a 2D representation of a point, stored as a single struct thus:
struct point2D {
    int row;
    int col;
} typedef point2D_t;

Complete the provided MIPS assembly below to make it equivalent to the C code above. Take care when calculating the addresses of the elements of the array, and when calculating the address of the height result.

# A topographic map!
# This helpful tool will tell explorers how much they need to climb to
# reach various points of interest.
#
# Given an array of points, `my_points`, it can look up individual cells
# in the 2D map and print their height.

# Constants
MAP_SIZE = 5
N_POINTS = 4

.text

main:
	# Registers:
	#   - $t0: int i, the loop counter
	#   - $t1: row of the current point
	#   - $t2: col of the current point
	#   - $t3: height of the current point
	#   - $t4: temporary result for array indexing
	#   - $t5: temporary result for array indexing

					# Loop over all elements, and print their data
points_loop_init:			# for (int i = 0; i < N_POINTS; i++) {
	li	$t0, 0			# $t0 = 0

points_loop_cond:
	bge	$t0, N_POINTS, points_loop_end	# if (i >= N_POINTS)

					# TODO: Complete these three!
					# int row = my_points[i].row;
					# int col = my_points[i].col;
					# int height = topography_grid[row][col];

					# printf("Height at %d,%d=%d\n", row, col, height);

	li	$v0, 4			# $v0 = 4 (print string)
	la	$a0, height_str		# load address of height_str into $a0
	syscall				# print height_str

	li	$v0, 1			# $v0 = 1 (print int)
	move	$a0, $t1		# $a0 = row
	syscall				# print row

	li	$v0, 11			# $v0 = 11 (print ASCII character)
	li	$a0, ','		# $a0 = ','
	syscall				# print ','

	li	$v0, 1			# $v0 = 1 (print int)
	move	$a0, $t2		# $a0 = col
	syscall				# print col

	li	$v0, 11			# $v0 = 11 (print ASCII character)
	li	$a0, '='		# $a0 = '='
	syscall				# print '='

	li	$v0, 1			# $v0 = 1 (print int)
	move	$a0, $t3		# $a0 = height
	syscall				# print height

	li	$v0, 11			# $v0 = 11 (print ASCII character)
	li	$a0, '\n'		# $a0 = '\n'
	syscall				# print '\n'

points_loop_iter:
	addi	$t0, $t0, 1		# i++
	b	points_loop_cond	# branch to points_loop_cond

points_loop_end:

	jr	$ra			# return 0;

.data

# 2D grid representing the height data for an area.
topography_grid:
	.word	0, 1, 1, 2, 3
	.word	1, 1, 2, 3, 4
	.word	1, 2, 3, 5, 7
	.word	3, 3, 4, 5, 6
	.word	3, 4, 5, 6, 7

# Points of interest to print heights for, as a 1D array of point2D_t structs.
# Note the memory layout of this array: each element requires 8 bytes, not 4.
my_points:
	.word	1, 2
	.word	2, 3
	.word	0, 0
	.word	4, 4

height_str: .asciiz "Height at "

Challenge exercise, for those who have seen linked data structures in C.

Consider a linked list

which could be defined in MIPS as:

    .data
list:   .word node1
node1:  .word 6, node2
node2:  .word 4, node3
node3:  .word 5, node4
node4:  .word 2, 0

Write a MIPS function that takes a pointer to the first node in the list as its argument, and returns the maximum of all of the values in the list. In other words, write a MIPS version of this C function:

typedef struct _node Node;
struct _node { int value; Node *next; };

int max (Node *list)
{
    if (list == NULL) return -1;
    int max = list->value;
    Node *curr = list;
    while (curr != NULL) {
        if (curr->value > max)
            max = curr->value;
        curr = curr->next;
    }
    return max;
}

You can assume that only positive data values are stored in the list.

FIFO queues can be implemented using circular arrays. For example:

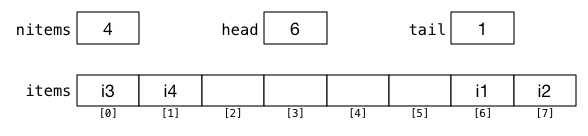
And the C code to manipulate such a structure could be:

// place item at the tail of the queue
// if queue is full, returns -1; otherwise returns 0
int enqueue (int item)
{
    if (nitems == 8) return -1;
    if (nitems  > 0) tail = (tail + 1) % 8;
    queue[tail] = item;
    nitems++;
    return 0;
}

// remove item from head of queue
// if queue is empty, returns -1; otherwise returns removed value
int dequeue (void)
{
    if (nitems == 0) return -1;
    int res = queue[head];
    if (nitems  > 1) head = (head + 1) % 8;
    nitems--;
    return res;
}

Assuming that the items in the queue are ints, and the following MIPS data definitions are used:

nitems: .word 0
head:   .word 0
tail:   .word 0
items:  .space 32

... implement the enqueue() and dequeue() functions in MIPS.

Use one of the standard function prologues and epilogues from lectures.

Revision questions

The following questions are primarily intended for revision, either this week or later in session.
Your tutor may still choose to cover some of these questions, time permitting.

Give MIPS directives to represent the following variables:
1. int v0;
2. int v1 = 42;
3. char v2;
4. char v3 = 'a';
5. double v4;
6. int v5[20];
7. int v6[10][5];
8. struct { int x; int y; } v7;
9. struct { int x; int y; } v8[4];
10. struct { int x; int y; } *v9[4];
Assume that we are placing the variables in memory, at an appropriately aligned address, and with a label which is the same as the C variable name.

If we execute the following small MIPS program:

   .data
x: .space 4
   .text
   .globl main
main:
   li  $a0, 32768
   li  $v0, 1
   syscall
   sw  $a0, x
   lh  $a0, x
   li  $v0, 1
   syscall
   jr  $ra

... we observed that the first syscall displays 32768, but the second syscall displays -32768. Why does this happen?