UNSW Prolog Programmer's Manual

TERMS

Constants include integers, floating point numbers and atoms such as:

	fred   prolog   =   <=  'Hello there'   []

The symbol for an atom can be any sequence of characters. Quotes should be used if there is a possibility of confusion with other symbols (such as variables, integers).

All variables must begin with a capital letter or '_', eg.

	X
	List
	G001
	_3
	_RESULT

If a variable is only needed once, it does not need a name Instead it may be written as an 'anonymous' variable indicated by a single underline character: '_'

A variable stands for some definite but unidentified object. Unlike other programming languages, a variable in Prolog is not a storage location. It is just name given to some value.

Data structures in Prolog are built from compound terms. A compound term consists of a function name (also called the principal functor) and a sequence of one or more arguments. A compound term also has an "arity" i.e. the number of arguments. For example the compound term whose name is "point and which has an arity of 3, with arguments X, Y and Z, is written as:

	point(X, Y, Z)

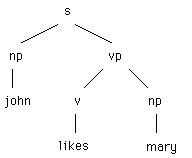
Compound terms can be pictured as trees. For example, the term:

	s(np(john), vp(v(likes), np(mary)))

would be pictured as the structure:

For convenience, some compound terms can be written using operators. For example, the following notation

	X + Y
	(P | Q)
	X < Y + 
	P;

is used instead of:

	+(X, Y)
	|(P, Q)
	<(X, +(Y, X))
	;(P)

Operators are described in more detail below.

An important class of data structures are the lists. A list is either the atom:

	[]

representing the empty list, or is a compound term with two arguments which are the head and tail of the list. A list of the first three natural numbers could be written as:

	list(1, list(2, list(3, [])))

but this can be very cumbersome. Instead we use the specia notation:

	[1, 2, 3]

When the tail of the list is a variable, we use the following notation:

	[X | L]
	[a, b | L]

This says that X is the head of the first list and L is the tail. In the second list, "a" and "b" are the first two arguments and L is the remainder of the list.

OPERATORS

	a + b / c	a + (b / c)

are equivalent. Parentheses are necessary if you want to write:

	(a + b) / c

If there are two operators in the subexpression which have the same precedence, the ambiguity must be resolved from the types of the operators. The possible types for an infix operator are:

	xfx	xfy	yfx

With an operator of type "xfx", the two subexpressions which are the arguments of the operator must be of lower precedence than the operator itself, unless the subexpression is explicitly bracketed (which gives it zero precedence). With an operator of type 'xfy', only the first or left-hand subexpression must be of lower precedence; the second can be of the same precedence as the main operator; and vice versa for an operator of type 'yfx'.

For example, if the operators '+' and '-' both have type "yfx" and are of the same precedence, then the expression:

	a - b + c

means:

	(a - b) + c

If the operators had type "XFY" the expression would mean:

	a - (b + c)

The possible types for a prefixoperator are:

	fx	fy

and for a postfix operator theyare:

	xf	yf

The meaning of the types shoul be clear by analogy with those for infix operators. As an example, if '-' were declared as a prefix operator of type 'fy', then:

	- - P

would be permissible. If the type were 'fx',the preceding expression would not be legal, although:

	- P

would still be a permissible form.

In Prolog, a functor named 'Name' is declared a an operator of type 'Type' and precedence 'Precedence' by the command:

	op(Precedence, Type, Name)!

The argument name can also be a list of names of operators of the same type and precedence.

It is possible to have more than one operator of the same name, so long different kinds, ie. infix, prefix or postfix. An operator of any kind may be redefined by a new declaration of the same kind. This applies equally to operators which are provided as standard in Prolog, namely:

	op(1200, xfx, :-)!
	op(1200,  fx, [:-, ?-])!
	op(1200,  xf, [?, !])!
	op(1100, xfy, ['|', ';'])!
	op(1050, xfy, ->)!
	op(700, xfx, [=, ==, /=, is, <, >, <=, >=])!
	op(700, fx, [load, unload, trace, untrace])!
	op(500, yfx, [+, -])!
	op(500, fx, [+, -])!
	op(400, yfx, [*, /])!
	op(300, xfx, mod)!

Note that the arguments of a compound term written in standard syntax must be expressions of precedence below 1000. Thus it is necessary to bracket the expression 'P :- Q' in:

	assert((P :- Q))

Note carefully the following syntax restrictions, which serve to remove potential ambiguity associated with prefix operators.

In a term written in standard syntax, the principal functor and its following '(' must not be separated by any intervening spaces, newlines etc. Thus:

	point  (X, Y, Z)

is invalid syntax.

If the argument of a prefix operator starts with a '(', this '(' must be separated from the operator by at least one space or other non-printable character. Thus:

	-(1+2)

is invalid syntax, and must be written as eg.

	-  (1+2)

If a prefix operator is written without an argument, as an ordinary atom, the atom is treated as an expression of the same precedence as the prefix operator, and must therefore be bracketed where necessary. Thus the brackets are necessary in:

	X = (-)

A further source of ambiguity in Prolog is arises from the ability to define infix and prefix operators with the same name. In some Prolog systems, these operators would be considered identical. In this Prolog, this is not the case. For example, in C, there is a prefix operator '++' and also a postfix operator '++' which have slighlty different functions. If we declare:

	op(300, fx, ++)!
	op(300, xf, ++)!

then we are creating two completely distinct atoms (which are also distinct from the referred to outside of its normal context as a principal functor of a compound term then, the operator must be preceded by a type name. For example:

	X =.. [infix +, 1, 2]?
	X = 1 + 2

This uses the infix operator '+' to create a new compound term using the 'univ' predicate. Similarly:

	X =.. [prefix ++, x]?
	X = ++ x

 	X =.. [postfix ++, x]?
	X = x ++

ARITHMETIC EXPRESSIONS

Each evaluable functor stands for an arithmetic operation. The evaluable functors are as follows, where X and Y are integer expressions:-

X + Y

integer addition

X - Y

integer subtraction

X * Y

integer multiplication

X / Y

integer division

X ^ Y

exponentiation (Y > 0).

X mod Y

X modulo Y

-X

unary minus

In the arithmetic built-in procedures which follow, X and Y stand for arithmetic expressions and Z for some term.

Z is X

Integer expression X is evaluated and the result is unified with Z. Fails if X is not an integer expression.

X == Y

The values of X and Y are equal.

X /= Y

The values of X and Y are not equal.

X < Y

The value of X is less than the value of Y.

X > Y

The value of X is greater than the value of Y.

X <= Y

The value of X is less than or equal to the value of Y.

X >= Y

The value of X is greater than or equal to the value of Y.

META-LOGICAL PREDICATES

(X, Y)

The logical AND of X and Y.

X | Y also X; Y

The logical OR of X and Y.

X = Y

Defined as if by clause ' Z = Z. '.

length(L, N)

L must be instantiated to a list of determinate length. This length is unified with N.

bagof(V, P, L)

Find all terms, V, such that P is true. Append V to the list, L. Bagof uses backtracking to find all the solutions to P.

!

All choice points so far in the current procedure call are forgotten.

not(P)

If the goal P has a solution, fail, otherwise succeed. It is defined as if by:-

	not(P) :- P, !, fail
	not(_).

P -> Q | R also P -> Q; R

Analogous to "if P then Q else R" i.e. defined as if by:

	P -> Q | R :- P, !, Q.
	P -> Q | R :- R.

P -> Q

When occurring other than as one of the alternatives of a disjunction, is equivalent to:

	P -> Q | fail.

repeat

Generates an infinite sequence of bactracking choices. It behaves (but doesn't use memory) as if defined by the clauses:

	repeat.
	repeat :- repeat.

fail

Always fails.

true

Always succeeds.

var(X)

Tests whether X is currently instantiated to a variable.

nonvar(X)

Tests whether X is currently instantiated to a non-variable term.

atom(X)

Checks that X is currently instantiated to an atom (ie. a non-variable term of arity 0, other than an integer).

integer(X)

Checks that X is currently instantiated to an integer.

atomic(X)

Checks that X is currently instantiated to an atom or integer.

functor(T, F, N)

The principalfunctor of term T has name F and arity N, where F is either an atom or, provided N is 0, an integer. Initially, either T must be instantiated to a non-variable, or F and N must be instantiated to, respectively, either an atom and a non-negative integer or an integer and 0. If these conditions are not satisfied, an error message is given. In the case where T is initially instantiated to a variable, the result of the call is to instantiate T to the most general term having the principal functor indicated.

arg(I, T, X)

Initially, I must be instantiated to a positive integer and T to a compound term. The result of the call is to unify X with the Ith argument of term T. (The arguments are numbered from 1 upwards.) If the initial conditions are not satisfied or I is out of range, the call merely fails.

X =.. Y

Y is a list whose head is the atom corresponding to the principal functor of X and whose tail is he argument list of that functor in X. eg.:

	product(0, N, N - 1) =.. [product, 0, N, N - 1]

If X is instantiated to a variable, then Y must be instantiated to a list of determinate length whose head is atomic (ie. an atom or integer).

name(X, L)

If X is an atom or integer then L is a list of the characters of the name of X. eg.:-

	name(product, [p, r, o, d, u, c t])

If X is instantiated to a variable, L must be instantiated to a list of characters. eg.:-

	name(X, [f, r, e, d])?

name is defined in terms of concat and char.

concat(L, A)

The members of list L are concatenated to form the atom A. For example,

	concat([abc, def],  X)?
	X = abcdef
	concat([f, r, e, d, 12], X)?
	X = fred12

The members of L must be atoms or integers. If X is instantiated then its value is compared with the result of the concatenation.

char(I, A, C)

The Ith character of atom A is C. I and A must be instantiated.

X

If X is instantiated to a term which would be acceptable as body of a clause, the goal X is executed exactly as if that term appeared textually in place of the X. In particular, any cut ('!') occurring in X is interpreted as if it occurred in the body of the clause containing X. If X is not instantiated as described the clause fails.

assert(C)

The current instance of C is interpreted as a clause and is added to the current program (with new private variables replacing any uninstantiated variables). The position of the new clause within the procedure concerned is implementation-defined. C must be instantiated to a non-variable.

asserta(C)

Like 'assert(C)', except that the new clause becomes the first clause for the procedure concerned.

assertz(C)

Like 'assert(C)', except that the new clause becomes the last clause for the procedure concerned.

clause(P, Q)

P must be bound to a non-variable term, and the current program is searched for clauses whose head matches P. The head and body of those clauses are unified with P and Q respectively. If one of the clauses is a unit clause, Q will be unified with `true'.

retract(C)

The first clause in the current interpreted program that matches C is erased. C must be initially instantiated to a non-variable, and becomes unified with the value of the erased clause. The space occupied by the erased clause is recovered the next time backtracking occurs. Any attempt to use a clause which has been retracted will result in unpredicatable behaviour from Prolog!

retractall(P)

All clauses in the current program whose head matches P are 'retract'ed. P must be bound to a non-variable term.

pp A

Lists in the current output stream all the interpreted clauses for predicates with name A, where A is bound to an atom.

listing

Lists in the current output stream all the clauses in the current interpreted program.

numbervars(X, N, M)

Unifies each of the variables in term X with a special term, so that 'write(X)' prints each of those variables as '#I', where the Is are consecutive integers from N to M-1. N must be instantiated to an integer.

ancestors(L)

Unifies L with a list of ancestor goals for the current clause. The list starts with the parent goal and ends with the most recent ancestor coming from a 'call' in a compiled clause.

subgoal_of(S)

The goal 'subgoal_of(S)' is equivalent to the sequence of goals:-

	ancestors(L), in(S, L)

where the predicate 'in' successively matches its first argument with each of the elements of its second argument.

INPUT AND OUTPUT PREDICATES

	myfile
	'123'
	'fred.data'
	'fred/student_db'

When files are opened for input or output, iProlog maps the file into a window which is made visible on the desktop. All I/O errors normally cause a failure of the procedure performing the I/O. Warnings are issued on the standard dialogue.

End of file is signalled when the predicate 'eof' is true. Any more input requests for a file whose end has been reached return the atom 'end_of_file'.

load F

Instructs the interpreter to read-in the program which is in file F. A window named F is opened and the text in file F is read into it. This window is available for editing after the program has been loaded in by Prolog. When a directive is read it is immediately executed. When a clause is read it is put after any clauses already read by the interpreter for that procedure. When a file has been loaded, a predicate

file(F, Proc_List)

is asserted. Proc_List is a list of the procedures defined in F. If F had been loaded before, the previous definitions are removed before the file is reloaded.

unload F

Retracts all procedures defined in F (according to the contents of file(F, Proc_list)). Also retracts file(F, Proc_list).

file(F, Proc_List)

Both F and Proc_List must be uninstantiated. F is successively bound to the names of loaded files. Proc_List is bound to the list of procedure names defined in the respective files.

see(F)

An inputwindow named F is opened becomes the current input stream. If a file, F, exists, it is read into the window.

seeing(F)

F is unified with the name of the current input stream.

seen

Closes current input stream. The associated window is also closed.

tell(F)

An output window named F is opened becomes the current output stream. If a file, F, exists, it is read into the window.

telling(F)

F is unified with the name of the current output stream.

told

Closes the current output stream. The associated window is also closed.

eof

Becomes true when the end of the current input stream has been reached.

read(X)

The next term, delimited by a 'fullstop' (ie. a '.' followed by <cr> or a space), is read from the current input stream and unified with X. The syntax of the term must accord with current operator declarations. If a call 'read(X)' causes the end of the current input stream to be reached, X is unified with the term 'end_of-file'.

ratom(X)

The next lexical token on the current input stream is bound to X. eg,

	: ratom(X)?
	fred
	X = fred.
	: ratom(X)?
	123
	X = 123	% X is an integer
	: ratom(X)?
	<=
	 X = <=
	: ratom(X)?
	,
	X = ','

# X

The same as ratom(X) except that if backtracking occurs, X will be pushed back onto the input stream so that it can be re-read by subsequent ratoms or #'s. Warning: It is dangerous to mix character I/O with #.

ask(Question, Answer)

The user is prompted by the string Question. The next token on the input stream is bound to Answer. Question may also be a list whose elements are concatenated to form the question.

print(X, ...)

print will accept a variable number of arguments, printing each term on the same line. If an argument is a string (enclosed in '"') then the string is printed without quotes. This print may be used to output messages. A newline character is appended to the output. The special character sequences '\ n' and '\ t' are recognized as newline and tab respectively.

prin(, ...)

Same as print except no newline is appended.

write(X)

The term X is written to the current output stream according to current operator declarations. X is output in a form which is acceptable to the read predicate.

nl

A new line is started on the current output stream.

getc(X)

Unifies X with the next character in the current input stream.

skip(C)

Skips to just after the next character C.

putc(X)

The character X is output the the current output steam.

ascii(C, I)

If C is a single character atom, I is instantiated to the ascii code representing C. If C is a variable and I is an integer, C is instantiated to the appropriate single character atom

tab(N)

N spaces are output to the current output stream. N may be an integer expression.

TRACING

Tracing of procedure P is enabled by the command:-

	trace P!

A number of procedures may be traced by the command:

	trace [proc1, proc2, ...]!

Tracing is disabled by the command:

	untrace P!

and more than one procedure may be untraced by:

	untrace [proc1, proc2, ...]!

At the beginning of a line output by the trace procedure, Prolog prints either of the following:

	C>
	E<
	F<
	R>

'C' indicates that a procedure is being called for the first tim e. A line beginning with 'E' shows the interpreter exiting a clause after all the goals have been satisfied. 'F' indicates an exit from a clause due to a failure in satisfying a goal. After a failure, Prolog will attempt to redo a procedure call if there are alternative clauses left in the procedure definition. This is shown by an 'R'.

An example of tracing output is shown below:

	f(A, b) - g(A).
	g(A) :- A = a.
	g(c).
	trace [f, g]!
	f(c, B)?

	C|>f(c,b)
	C||>g(c)
	F||<g(c)
	R||>g(c)
	E||<g(c)
	E|<f(c,b)

	B = b.