CREATE TABLE Parts (
       id#     number(10) primary key,
       name    varchar(10),
       colour  varchar(5) check value in ('red','blue','green'),
       onhand  integer
);

The value d is the depth of the file i.e. the number of bits required in the hash value to address all pages in the file. For example, a file with 8 pages can be addressed with a 3-bit hash value (i.e. the possible hash values are 000, 001, 010, 011, 100, 101, 110, 111). Thus, the first step in determining the value for d is to work out how many pages are in the file.

The number of pages b is determined as follows:

b = ceil(r/C) = ceil(819,200/100) = ceil(8192) = 8192

What size of hash value does it take to address 8192 pages? If the file has 2ⁿ pages, then it requires an n-bit hash value. For this example:

d = ceil(log₂b) = ceil(log₂8192) = ceil(13) = 13

Thus we have a 13-bit hash value for each record that is produced via an interleaving of bits from the four attributes id#, name, colour, onhand. The next step is to determine how many bits d_i each attribute A_i contributes to this record hash value.

We use the following kinds of information to decide this:

• the likelihood of an attribute being used in a query
  Recall that the more bits that an attribute contributes, then the more pages we need to search when the attribute is not used in a query (i.e. we have more unknown * bits). Thus, in order to minimise query costs, we should allocate more bits to attributes that are more likely to be used in queries and less bits to attributes that are more likely to be missing from queries.

• the number of distinct values in the attribute domain
  If a domain has n distinct values, then a perfect hash function can distinguish these values using log₂n bits. If we allocate more bits to this attribute, they will not be assisting with the primary function of hashing, which is to partition distinct values into different pages.

• the discriminatory power of the attribute
  The discriminatory power of an attribute measures the likely number of pages needed to be accessed in answering a query involving that attribute. For example, a query involving a primary key has a solution set that consists of exactly one record, located on one page of the data file; in the best case (e.g. hashing solely on the primary key, we would access exactly one page of the data file in answering such a query). We would tend to allocate more bits to very discriminating attributes because this reduces the number of pages that need to be accessed in finding the small answer set in queries involving such attributes.

Let us consider each attribute in turn in terms of these characteristics:

• id# number(10) primary key

  • This attribute is used in only one query, which occurs 25% of the time, so its overall likelihood of use is 0.25. This suggests that we should not allocate too many bits to it.

  • Since each id# is a 10-digit number, there are 10¹⁰ possible part id's. This is a very large domain, with around 2³⁴ distinct values. Thus, the domain size puts no restriction on the number of bits that we might allocate to this attribute.

  • This attribute is very discriminatory. In fact, if it is used in a query, then we know that there will be either 0 or 1 matching records. This suggests that we should allocate it many bits, so as to avoid searching many unnecessary pages when this attribute is used in a query.

• name varchar(10)

  • This attribute is used in only one query, which occurs 50% of the time. Its overall likelihood of use is thus 0.5. This suggests that we should allocate a reasonable number of hash bits to this attribute.

  • The name attribute is an arbitrary string giving a descriptive name for each part. Given the semantics of the problem, there will be names such as "nut", "washer", "bolt", "joint", and so on. There could quite conceivably be up to 10000 different part names. In this case, 13 bits (2¹³=8192) of information would be sufficient to give a different hash value for each of these names. Thus, it would not be worth allocating more than 10 bits to this attribute.

  • If we assume that there are around 8000 part names, and we know that there are 819,200 parts, then, assuming a uniform distribution of part names, each name would occur around 1000 times in the database. In other words, a query based solely on the name attribute would select around 1000 tuples. This attribute is moderately discriminating, which suggests that we should not allocate too many bits to it.

• colour varchar(5) in ('red','blue','green')

  • This attribute is used in two queries, whose likelihoods are 50% and 25% respectively. Overall, this attribute is 75% likely to occur in a query. This suggests that we should allocate most bits to it.

  • There are only three possible values for the colour attribute. These values can be distinguished using only 2 bits of information, therefore there is no point in allocating more than 2 bits to this attribute.

  • If there are 3 colours and 819,200 records, then, assuming a uniform distribution of colours, each colour value will occur in around 27,000 different records. Thus, colour is not a discriminating attribute and we are not required, on the basis of this characteristic, to allocate it many bits.

• onhand integer

  • This attribute is not used in any queries, and so there is no point allocating it any bits. If we do, these bits will always be unknown, and we a guaranteeing a fixed unnecessary overhead in every query.

  • There are a large number of possible values for this numeric attribute, and so there is no upper bound on the number of bits to allocate. Of course, the non-usage of this attribute in queries suggests that we don't allocate it any bits, so an upper-bound is not an issue.

  • It is difficult to estimate the discriminatory power of this attribute. For a given onhand quantity, there may be a large number of parts with this quantity, or there may be none.

The usage of an attribute is the most important property in determining how many bits to allocate to it. This should be modified by any upper bound suggested by the domain size. Finally, discriminatory power may suggest extra bits to be allocated to an attribute, but it more likely an indication that some other indexing scheme (than multi-attribute hashing) should be used. For example, if the most common kind of query was a selection based on the id#, then it would be sensible to use a primary key indexing scheme such as a B-tree in preference to multi-attribute hashing.

The frequency of usage suggests that we allocate most bits to colour, less bits to name, less bits to id#, and no bits to onhand. However, the domain size of colour indicates that it should not be allocated more than 2 bits. This fixes the bit allocations for two attributes: d_colour = 2 and d_onhand = 0. This leaves 11 more bits from the original d = 13 to allocate. Usage frequency suggests that we allocate more to name, but discriminatory power suggests that we allocate as many bits as possible to id#.

According to the optimisation criteria mentioned in lectures, the lowest average cost would likely be obtained if d_name is the larger, so we could set d_name = 6 and d_id# = 5. These allocations give the following average query cost:

Cost = pq1Costq1 + pq2Costq2 + pq3Costq3
     = 0.25 * 28 + 0.5 * 25 + 0.25 * 211
     = 592 page accesses

where there are 5 known bits (6+2=8 unknown bits) for query type q1, 6+2=8 known bits (5 unknown bits) for query type q2, and 2 known bits (5+6=11 unknown bits) for query type q3.

However, it turns out that an alternative bit-allocation has even better cost: d_name = 5 and d_id# = 6.

Cost = pq1Costq1 + pq2Costq2 + pq3Costq3
     = 0.25 * 27 + 0.5 * 26 + 0.25 * 211
     = 576 page accesses

As far as the choice vector is concerned, there is no particular reason not to simply interleave the hash bits from each of attributes in forming the hash value for each record, thus giving:

d = 13    d_id# = 6    d_name = 5    d_colour = 2    d_onhand = 0

cv₀ = bit_id#,0   cv₁ = bit_name,0   cv₂ = bit_colour#,0   cv₃ = bit_id#,1   cv₄ = bit_name,1   cv₅ = bit_colour,1   cv₆ = bit_id#,2   etc.

where bit_A,n refers to the n^th bit of the hash value h(A) for attribute A.

Student(id:integer, name:string, address:string,
        age:integer, course:string, gpa:real);

select * from Student where course='BSc' and age=20;

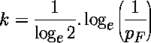
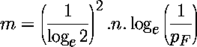
Before we can answer the question we need to work out the characteristics of the signatures. This comes from the following:

• n = 6 attributes
• r = 40,000 records
• B = 1024 bytes/block
• C = 20 recs/block
• p_F = 10^-4

For record signatures, we use the formulae:

• k = log_e(1/p_F) / (log_e2)
• m = n * log_e(1/p_F) / ((log_e2)²)

Putting the above values into these formulae gives: k = 13 (rounded) and m = 116.

Now, 116 bits is 14 bytes, which doesn't divide nicely into the block size (1024 bytes), and neither is it a multiple of 4-bytes, so we may have to worry about alignment problems (ints not aligned on 4-byte address boundaries). In this case, it's better to simply increase the size of each signature to 16 bytes (i.e. set m = 128)

For block (page) signatures, we use the formulae:

• k = log_e(1/p_F) / (log_e2)
• m = n * C * log_e(1/p_F) / ((log_e2)²)

Putting the above values into these formulae gives: k = 13 and m = 2301.

Now, 2301 bits is 288 bytes, which doesn't fit at all nicely into 1024-byte pages. We could have only 3 signatures per page, with a lots of unused space. In such as case it might be better to reduce the size of block signatures to 256 bytes, so that 4 signatures fit nicely into a page. This effectively makes m = 2048. The effect of this is to increase the false match probability p_F from 1*10^-4 to 3*10^-4. For the convenience of the signature size, this seems an acceptable trade-off (this is still a very small chance of getting a false match).

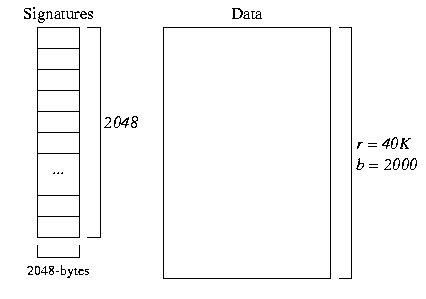
1. Record signatures

   The file structure for a record-based signature file with m=128 looks as follows:

   

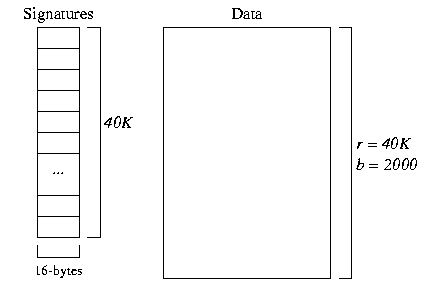
   In the data file, there are 40,000 records in b = 40,000/20 = 2000 pages In the signature file, there are 40,000 * 128-bit (16-byte) signatures. We can fit 64 * 16-byte signatures in a 1024-byte page, so this means there are 625 pages of signatures.

   To answer the select query we need to do the following:

   • for a 16-byte query descriptor
   • read all of the record signatures, comparing against the query descriptor
   • read blocks containing candidate records
   Note that some of the candidates will be false matches. We can work out how many simply by noting that there are 40,000 records and the likelihood of any one being a false match is 10^-4. This leads to around 4 false matches per query. Let us assume that there are M genuine matching records, and make the worst-case assumption that every candidate record will come from a different block. The overall cost will thus be:
   Cost_select = 625 + M + 4 page reads

2. Block signatures

   The file structure for a block-based signature file with m=2048 looks as follows:

   

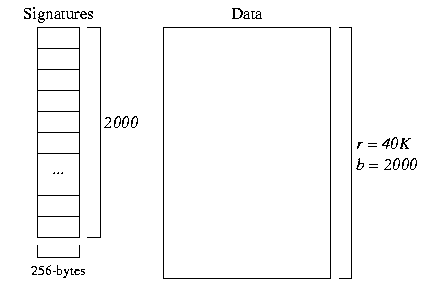
   The data file is as before. In the signature file, there are 2000 * 2048-bit (256-byte) block signatures. We can 4 signatures in 1 1024-byte page, so this means we need 500 pages of signatures.

   To answer the select query we need to do the following:

   • form a 256-byte query descriptor
   • read all of the block signatures, comparing against the query descriptor
   • read candidate blocks suggested by the signatures
   As above, some of these will be false matches. In this case p_F = 3*10^-4 and there are 2000 signatures, so we'd expect only 1 false match. As before, let us assume that there are M genuine matching blocks. The overall cost will thus be:
   Cost_select = 500 + M + 1 page reads

3. Bit-sliced block signatures

   For the bit-sliced signature file, we take the 2000 * 2048-bit block signatures from the previous file organisation and "tip them on their side", giving us 2048 * 2000-bit signature slices. Now, dealing with a 2000-bit quantity is inconvenient; once again, it doesn't fit nicely into 1024-byte blocks and so a suitable modification would be to make the slices 2048-bits long. This means simply that we can handle more data pages should the need arise; it doesn't change the false match probabilities. This gives a file structure that looks like:

   

   The data file is unchanged from the previous two cases.

   To answer the select query we need to do the following:

   • form a 256-byte query descriptor
   • iterate through the query descriptor, bit-by-bit
   • for each 1 bit that we find, read the corresponding bit-slice
   • iterate through the result slice, fetching candidate pages

   The primary cost determinant in this case is how many slices we need to read. This will be determined by how many 1-bits are set in the query descriptor. Since each attribute sets k=13 bits, and we have two attributes contributing to the query descriptor, we can have at most 26 bits set in the query descriptor. This means we will need to read 26 descriptor slices to answer the query. As well as descriptors, we need to read M candidate blocks containing genuine matching records, along with 1 false match candidate block.

   The overall cost will thus be:

   Cost_select = 26 + M + 1 page reads

(3,4,5)   (2,4,6)   (2,3,4)   (3,5,6)   (4,3,2)   (2,6,5)   (4,5,6)   (1,2,3)

Start by computing some (partial) hash values (bottom 8 bits is (more than) enough):

    Tuple       MA-hash Value
    (3,4,5)     ...01001101
    (2,4,6)     ...11001000
    (2,3,4)     ...00101010
    (3,5,6)     ...11001011
    (4,3,2)     ...10110010
    (2,6,5)     ...01101100
    (4,5,6)     ...11010010
    (1,2,3)     ...10100101

Insert (3,4,5) ... use least-significant bit = 1 to select page; insert into page 1

Page[0]: empty  <- SP
Page[1]: (3,4,5)

Insert (2,4,6) ... use least-sig bit = 0 to select page; insert into page 0

Page[0]: (2,4,6)  <- SP
Page[1]: (3,4,5)

Insert (2,3,4) ... use least-sig bit = 0 to select page; insert into page 0

Page[0]: (2,4,6) (2,3,4)  <- SP
Page[1]: (3,4,5)

Insert (3,5,6) ... 3 insertions since last split => split page 0 between pages 0 and 2

Page[0]: (2,4,6)
Page[1]: (3,4,5)  <- SP
Page[2]: (2,3,4)

then use least-sig bit = 1 to select page; insert into page 1

Page[0]: (2,4,6)
Page[1]: (3,4,5) (3,5,6)  <- SP
Page[2]: (2,3,4)

Insert (4,3,2) ... use least sig-bit = 0, but <SP, so take 2 bits = 10 to select page

Page[0]: (2,4,6)
Page[1]: (3,4,5) (3,5,6)  <- SP
Page[2]: (2,3,4) (4,3,2)

Insert (2,6,5) ... use least sig-bit = 0, but <SP, so take 2 bits = 00 to select page

Page[0]: (2,4,6) (2,6,5)
Page[1]: (3,4,5) (3,5,6)  <- SP
Page[2]: (2,3,4) (4,3,2)

This make 3 insertions since the last split => split again
Add new page [3] and partition tuples between pages 1 and 3
Also, after splitting, the file size is a power of 2 ...
So we reset SP to 0 and increase depth to d=2

Page[0]: (2,4,6) (2,6,5)  <- SP
Page[1]: (3,4,5)
Page[2]: (2,3,4) (4,3,2)
Page[3]: (3,5,6)

Insert (4,5,6) ... use 2 bits = 10 to select page
but page 2 already full => add overflow page

Page[0]: (2,4,6) (2,6,5)  <- SP
Page[1]: (3,4,5)
Page[2]: (2,3,4) (4,3,2)  -> Ov[0]: (4,5,6)
Page[3]: (3,5,6)

Insert (1,2,3) ... use 2 bits = 01 to select page 1

Page[0]: (2,4,6) (2,6,5)  <- SP
Page[1]: (3,4,5) (1,2,3)
Page[2]: (2,3,4) (4,3,2)  -> Ov[0]: (4,5,6)
Page[3]: (3,5,6)