Consider the relations:

Student(id#, name, age, course)
Subject(code, title, description)

Make the following assumptions:

• r_Student = 50,000,   r_Subject = 5,000
• the data file for Student is sorted on id#, the data file for Subject is sorted on code
• simple one-level indexes are used (e.g. because the files are reasonably static)
• record IDs (RIDs) are 4-bytes long
• all data pages and index pages are 4KB long

Based on these assumptions, answer the following:

1. You can build a dense index on any field. Why?

   [show answer]

   A dense index has one index entry for each data record. It is required that the entries in the index are sorted (to make searching the index efficient). However, there are no specific requirements on where the records are located within the data file. Thus, you can build a dense index on any or all fields.

2. On which field(s) could you build a non-dense index?

   [show answer]

   A non-dense index has one entry per block, and assumes that all records in that block have key values less than all key values in the next block. Thus, you can only build non-dense indexes on a field (key) on which the relation is sorted.

3. If the student id# is a 4-byte quantity, how large would a dense index on Student.id# be?

   [show answer]

   A dense index has one entry per data record, so we have 50,000 entries. Each index entry contains a copy of the key value and the address of the page where the record containing that key is stored. Index entries will thus have 4-bytes for the id# and 4-bytes for the page address, so we can fit floor(4096/8) = 512 index entries per page. The number of index pages required is then ceil(50000/512) = 98.

4. If the subject code is an 8-byte quantity, how large would a dense index on Subject.code be?

   [show answer]

   Same reasoning as for previous question. 5,000 index entries. Each index entry contains 8-bytes (for subject code) + 4 bytes for page address. Each index page contains floor(4096/12) = 341 index entries. And so the number of index pages is ceil(5000/341) = 15.

5. If the c_Student = 100 and c_Subject = 20, and other values are as above, how large would non-dense indexes on Student.id# and Subject.code be?

   [show answer]

   For a non-dense index, we need only one index entry per block of the data file. Assuming that the files are fully compacted, the Student file has ceil(50000/100) = 500 blocks, and the Subject file has ceil(5000/20) = 250 blocks. The analysis then proceeds as for the previous question, except with one index entry per block.

   Thus #index blocks for Student = ceil(500/512) = 1, and #index blocks for Subject = ceil(250/341) = 1

6. If you had just dense indexes on Student.id# and Subject.code, briefly describe efficient processing strategies for the following queries:

   1. select name from Student where id=2233445
   2. select title from Subject where code >= 'COMP1000' and code < 'COMP2000'
   3. select id#,name from Student where age=18
   4. select code,title from Subject where title like '%Comput%'

   [show answer]

   1. select name from Student where id=2233445

      Do a binary search through the index (max log₂98=7 page reads) to find the entry for 2233445 and then fetch the data block containing that record (if it exists).

   2. select title from Subject where code >= 'COMP1000' and code < 'COMP2000'

      Do a binary search through the index (max log₂15=4 page reads) to find the page for COMP1000 (or nearest similar subject), and then do a scan through the data file to grab all the COMP1xxx records, which will appear consecutively.

   3. select id#,name from Student where age=18

      Since the index provides no assistance, the simplest solution is probably just to scan the entire file and select the 18-year-olds as you go. Sorting the file doesn't help here.

   4. select code,title from Subject where title like '%Comput%'

      Once again, the index doesn't help, so a linear scan is the only option.

7. What techniques could you use to improve the performance of each of the above queries? And how would it impact the other queries?

   [show answer]

   1. You could do better than the above by using either hashing (which would require only one page access) or a balanced tree index (e.g. B-tree), which would require at most three. Hashing would not be an option if there was some reason why the file had to be maintained in order on the student id.

   2. A balanced tree index like a B-tree on the code field would also help here.

   3. If this was a common kind of query (lookup by specific age), and if there was no requirement to keep the file in any particular order, you could hash the file on age to improve performance. A more likely scenario would be to add a dense index on the age field.

   4. You can't use an index to assist with this query, because it doesn't use a notion of "matching" that involves the natural ordering on the field values. The query could match "Intro to Computing" or "Computing 1A" or "Mathematical Computation" etc.

Consider a relation R(a,b,c,d,e) containing 5,000,000 records, where each data page of the relation holds 10 records. R is organized as a sorted file with the search key R.a. Assume that R.a is a candidate key of R, with values lying in the range 0 to 4,999,999.

Determine which of the following approaches to evaluating the relational algebra expression π_a,b(σ_a>50000(R)) is likely to be the cheapest (minimum disk I/O):

1. Use a clustered B+ tree index on attribute R.a.
2. Use a linear hashed index on attribute R.a.
3. Use a clustered B+ tree index on attributes (R.a,R.b).
4. Use a linear hashed index on attributes (R.a,R.b).
5. Use an unclustered B+ tree index on attribute R.b.
6. Access the sorted file for R directly.

[show answer]

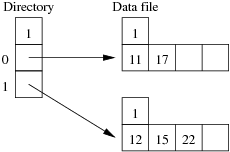
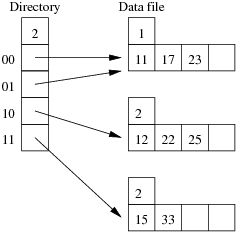
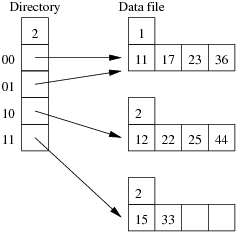
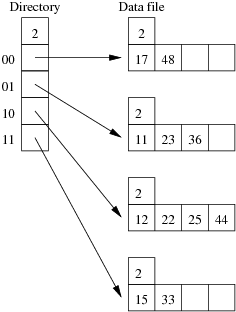
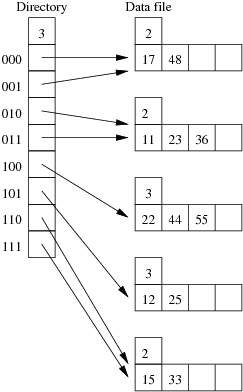
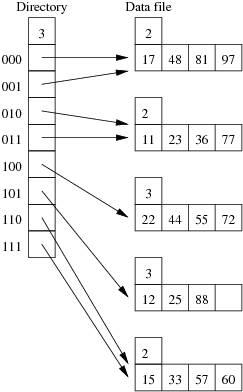
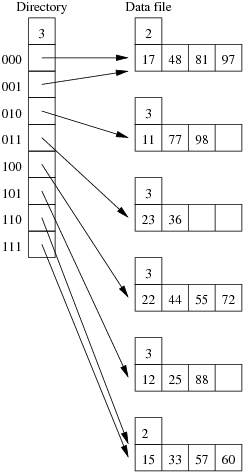
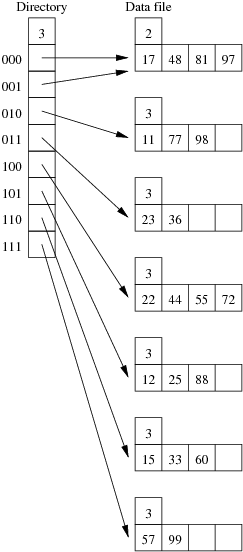
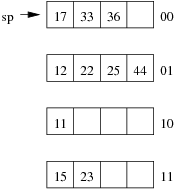
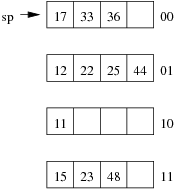
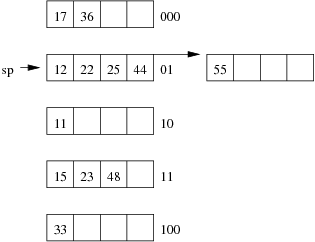
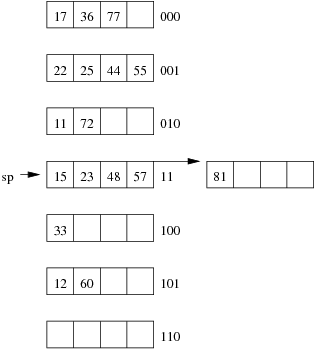
Consider the following example file organisation using extendible hashing. Records are inserted into the file based on single letter keys (only the keys are shown in the diagram).

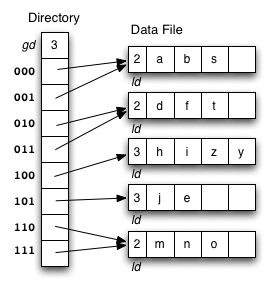
The dictionary contains a "global depth" value (gd), which indicates how many hash bits are being considered in locating data pages via the dictionary. In this example, the depth gd=3 and so the dictionary is size 2^gd=2^d=8.

Each data page is marked with a "local depth" value (ld), which indicates the effective number of bits that have been used to place records in that page. The first data page, for example, has ld=2, which tells us that only the first two bits of the hash value were used to place records there (and these two bits were 00). The third data page, on the other hand, has ld=3, so we know that all records in that page have their first three hash bits as 100.

Using the above example to clarify, answer the following questions about extendible hashing:

1. Under what circumstances must we double the size of the directory, when we add a new data page?

   [show answer]

   The directory has to be doubled whenever we split a page that has only one dictionary entry pointing to it. We can detect this condition via the test gd = ld.

2. Under what circumstances can we add a new data page without doubling the size of the directory?

   [show answer]

   We don't need to double the directory if the page to be split has multiple pointers leading to it. We simply make half of those pointers point to the old page, while the other half point to the new page. We can detect this condition via the test ld < gd.

3. After an insertion that causes the directory size to double, how many data pages have exactly one directory entry pointing to them?

   [show answer]

   Two. The old page that filled up and the new page that was just created. Since we just doubled the number of pointers in the dictionary and added only one new page, all other data pages now have two pointers leading to them.

4. Under what circumstances would we need overflow pages in an extendible hashing file?

   [show answer]

   If we had more than C_r records with the same key value. These keys would all have exactly the same hash value, no matter how many bits we take into account, so if we kept doubling the dictionary in the hope of eventually distinguishing them by using more and more bits, then the dictionary would grow without bound.

5. What are the best-case and worst-case scenarios for space utilisation in the dictionary and the data pages (assuming that there are no overflow pages)? Under what circumstances do these scenarios occur?

   [show answer]

   The best case scenario is when the hash function spreads the records uniformly among the pages and all pages are full. We then have 100% space utilisation in the data pages. Under the best-case scenario, each data page would have exactly one dictionary entry referring to it (i.e. gd == ld for every page).

   The worst case scenario is when we have an extremely skew hash function (e.g. the hash function maps every key value to the same page address ... at least in the first few hash bits). Let's assume that we fill up the first page and then add one more record. If we needed to consider all 32 bits of the hash before we could find one record that mapped to a different page (e.g. all records have hash value 0000...0000 except for one record that has hash value 0000...0001, then we would have a dictionary with 2³² entries (which is extremely large). At this point, the data page space utilisation would be just over 50% (we have two pages, one of which is full and the other of which contains one record). It is unlikely that an extendible hashing scheme would allow the dictionary to grow this large before giving up on the idea of splitting and resorting to overflow pages instead.

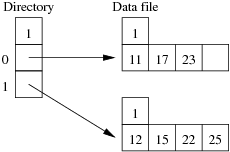
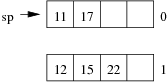
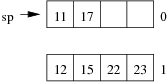
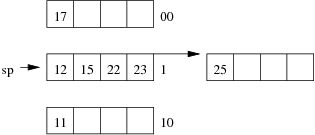
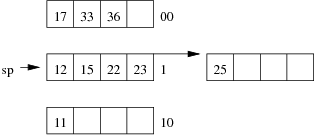
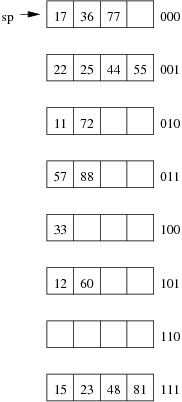
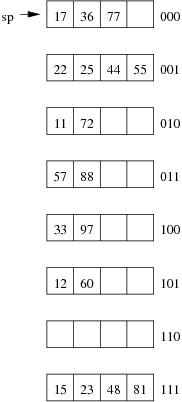
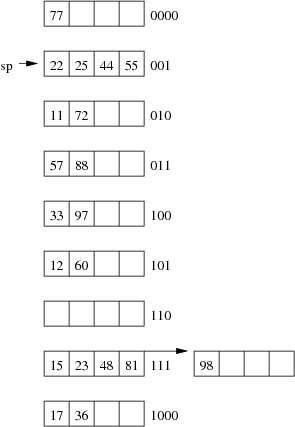
Consider the following example file organisation using linear hashing. Records are inserted into the file based on single letter keys (only the keys are shown in the diagram).

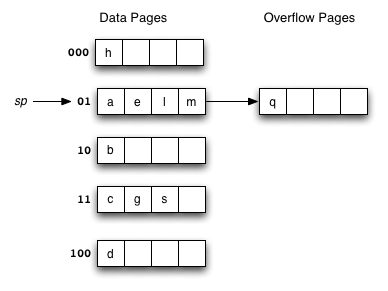
Using the above example to clarify, answer the following questions about linear hashing:

1. How is it that linear hashing provides an average case search cost of only slightly more than one page read, given that overflow pages are part of its data structure?

   [show answer]

   If we start from an file with 2^d pages, by the time the file size has doubled to 2^d+1 pages, we will have split every page in the first half of the file. Splitting a page generally has the effect of reducing the length of the overflow chain attached to that page. Thus, as the file size doubles, we will most likely have reduced the length of every overflow chain. In general, and assuming a reasonable hash function, this will keep the overflow chain lengths close to zero, which means that the average search cost will be determined by the fact that we normally read just a single data page from the main data file.

2. Under what circumstances will the average overflow chain length (Ov) not be reduced during page splitting?

   [show answer]

   If all of the records in a particular page have the same hash values in their lower-order d bits and lower-order d+1 bits, then splitting the page will leave them all where they were. It will also result in the newly-added page being empty.

3. If a linear hashing file holds r records, with C records per page and with splitting after every k inserts, what is the worst-case cost for an equality search, and under what conditions does this occur?

   [show answer]

   The worst-case occurs when all of the keys map to the same page address. If this occurs, and the file contains r records, then they will all have been attached to e.g. the first page. This will mean that there's a primary data page plus overflow chain containing ceil(r/C) pages. This will be the cost of a search. If the file starts out with a single data page, then there will have been floor(r/k) new data pages added due to splitting after every k insertions. This means that the file contains floor(r/k)+1 data pages, and all but one of them is empty.

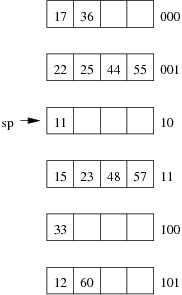
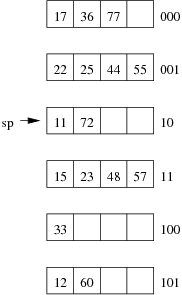
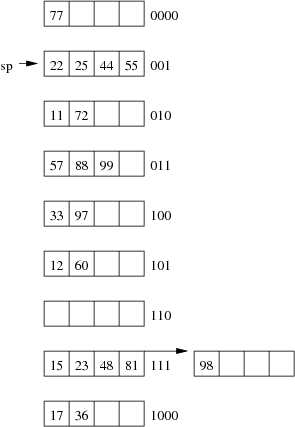
Consider the following employee relation:

Employee(id#:integer, name:string, dept:string, pay:real)

and some records from this relation for a small company:

(11, 'I. M. Rich', 'Admin',    99000.00)
(12, 'John Smith', 'Sales',    55000.00)
(15, 'John Brown', 'Accounts', 35000.00)
(17, 'Jane Dawes', 'Sales',    50000.00)
(22, 'James Gray', 'Sales',    65000.00)
(23, 'Bill Gates', 'Sales',    35000.00)
(25, 'Jim Morris', 'Admin',    35000.00)
(33, 'A. D. Mine', 'Admin',    90000.00)
(36, 'Peter Pipe', 'R+D',      30000.00)
(44, 'Jane Brown', 'R+D',      30000.00)
(48, 'Alex Brown', 'Plant',    40000.00)
(55, 'Mario Reid', 'Accounts', 27000.00)
(57, 'Jack Smith', 'Plant',    35000.00)
(60, 'Jack Brown', 'Plant',    35000.00)
(72, 'Mario Buzo', 'Accounts', 30000.00)
(77, 'Bill Young', 'Accounts', 31000.00)
(81, 'Jane Gates', 'R+D',      25000.00)
(88, 'Tim Menzie', 'R+D',      45000.00)
(97, 'Jane Brown', 'R+D',      30000.00)
(98, 'Fred Brown', 'Admin',    60000.00)
(99, 'Jane Smith', 'Accounts', 30000.00)

Assume that we are using the following hash function:

hash(11) = 01001010
hash(12) = 10110101
hash(15) = 11010111
hash(17) = 00101000
hash(22) = 10000001
hash(23) = 01110111
hash(25) = 10101001
hash(33) = 11001100
hash(36) = 01111000
hash(44) = 10010001
hash(48) = 00001111
hash(55) = 10010001
hash(57) = 11100011
hash(60) = 11000101
hash(72) = 10010010
hash(77) = 01010000
hash(81) = 00010111
hash(88) = 10101011
hash(97) = 00011100
hash(98) = 01010111
hash(99) = 11101011

Assume also that we are dealing with a file organisation where we can insert four records on each page (data page or overflow page) and still have room for overflow pointers, intra-page directories, and so on.

Show the insertion of these records in the order given above into an initially empty extendible hashing file. How many pages does the relation occupy (including the pages to hold the directory)?

[show answer]

Using the same data as for the previous question, show the insertion of these records in the order given above into an initially empty linear hashed file. How many pages does the relation occupy (including any overflow pages)?

[show answer]