You have an unsorted heap file containing 4500 records and a select query is asked that requires the file to be sorted. The DBMS uses an external merge-sort that makes efficient use of the available buffer space.

Assume that: records are 48-bytes long (including a 4-byte sort key); the page size is 512-bytes; each page has 12 bytes of control information in it; 4 buffer pages are available.

1. How many sorted subfiles will there be after the initial pass of the sort algorithm? How long will each subfile be?

   Answer:

   We need to first of all work out the blocking factor and then the number of data blocks. The available space for storing records in each page is 512-12=500 bytes, so each page can store up to 10 48-byte records. This means that 450 pages are needed to store the 4500 records.

   In the first pass, we read as many pages as we can into the available buffers, sort these page in memory, and then write them out. Given that 4 buffer pages are available, there will be ceil(450/4)=113 sorted runs (sub-files) of 4 pages each, except the last run which is only 2 pages long.

2. How many passes (including the initial pass considered above) will be required to sort this file?

   Answer:

   After pass 0, we have N=ceil(b/B) sorted runs, each of length B. Subsequent merging passes will increase the length of the sorted runs by B-1 times on each pass. The number of merging passes until the whole file is sorted is ceil(log_B-1N).

   For this scenario, b=450, B=4, N=113 so #passes = 1 + ceil(log_4-1113) = 6.

3. What will be the total I/O cost for sorting this file?

   Answer:

   Each pass requires us to read and write every page in the file. The total number of I/O operations is thus 2*b*#passes. The total cost for sorting this file is 2 * 450 * 6 = 5,400 I/Os.

4. What is the largest file, in terms of the number of records, that you can sort with just 4 buffer pages in 2 passes? How would your answer change if you had 257 buffer pages?

   Answer:

   We first need to work out the answer in terms of number of pages (b), and then convert to number of records.

   In pass 0, ceil(b/B) runs are produced. In pass 1, we must have enough buffers to enable us to merge this many runs, so B-1 must be larger or equal to ceil(b/B). Given B, we can determine b by "solving" (B-1) ≥ ceil(b/B). Re-arranging the formula (with a few simplifying assumptions) gives b = B*(B-1).

   When B is given to be 4, b = 4*(4-1) = 12. The maximum number of records on 12 pages is 12*10=120.

   When B is given as 257, b= 257*256 = 65792, with 65792*10=657920 records.

For each of these scenarios:

1. a file with 10,000 pages and 3 available buffer pages.
2. a file with 20,000 pages and 5 available buffer pages.
3. a file with 2,000,000 pages and 17 available buffer pages.

answer the following questions assuming that external merge-sort is used to sort each of the files:

1. How many runs will you produce on the first pass?

   Answer:

   In the first pass (Pass 0), N=ceil(b/B) sorted runs, each B pages long, are produced (b is the number of file pages and B is the number of available buffer pages).

   1. ceil(10,000/3) = 3334 sorted runs
   2. ceil(20,000/5) = 4000 sorted runs
   3. ceil(2,000,000/17) = 117648 sorted runs

2. How many passes will it take to sort the file completely?

   Answer:

   The number of passes required to sort the file completely, including the initial sorting pass, is 1+ceil(log_B-1N), where N=ceil(b/B) is the number of runs produced from pass 0:

   1. 1+ceil(log_3-1(3334))  = 13 passes
   2. 1+ceil(log_5-1(4000)) = 7 passes
   3. 1+ceil(log_17-1(117648)) = 6 passes

3. What is the total I/O cost for sorting the file? (measured in #pages read/written)

   Answer:

   Since each page is read and written once per pass, the total number of pages I/Os for sorting the file is 2 * b * #passes:

   1. 2 * 10,000 * 13 = 26 * 10⁴
   2. 2 * 20,000 * 7 = 28 * 10⁴
   3. 2 * 2,000,000 * 6 = 24 * 10⁶

Consider processing the following SQL projection query:

	select distinct course from Students;

where there are only 10 distinct values (0..9) for Student.course, and student enrolments are distributed over the courses as follows:

Show the flow of records among the pages (buffers and files) when a hash-based implementation of projection is used to eliminate duplicates in this relation.

Assume that:

• each page (data file page or in-memory buffer) can hold 1000 records
• the partitioning phase uses 1 input buffer, 3 output buffers and the hash function (x mod 3)
• the duplicate elimination phase uses 1 input buffer, 4 output buffers and the hash function (x mod 4)

Answer:

In the partition phase, there are 3 partitions produced (because of the mod 3 hash function). The first contains records with course from the set 0,3,6,9; the second contains records with course from 1,4,7; the third partition contains records with course 2,5,8.

The following diagram shows the partitioning phase:

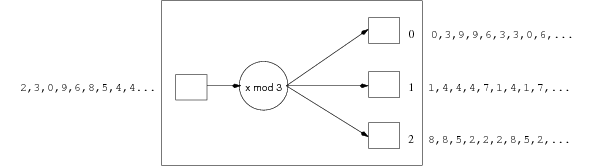
From the record counts, we can compute that the first partition contains 5,000+3,000+1,000+1,000 = 10,000 records. Given that that there are 1000 records per page, this makes 10 pages. The second partition contains 4,000+2,000+1,000 records, giving 7 pages. The third partition contains 5,000+1,000+2,000 records, giving 8 pages.

In the elimination phase, there are three stages, one to deal with each of the partitions.

In the first stage, we read back all of the 0,3,6,9 records and apply the mod 4 hash function. The first record with key=0 goes into buffer 0, and all other key=0 records are eliminated when they see the first one. The first record with key=3 goes into buffer 3, and all other key=3 records are eliminated when they see the first one. The first record with key=6 goes into buffer 2, and all other key=6 records are eliminated when they see the first one. The first record with key=9 goes into buffer 1, and all other key=9 records are eliminated when they see the first one. At the end of this stage, we can scan through the buffers and extract four distinct output records.

The following diagram shows the elimination phase for this first partition:

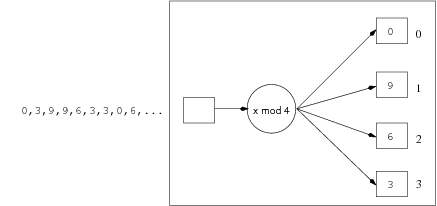
The second stage proceeds similarly, with key=1 records hashing to buffer 1, key=4 records hashing to buffer 0 and key=7 records hashing to buffer 3. Buffer 2 is unused.

The third stage proceeds similarly, with key=2 records hashing to buffer 2, key=5 records hashing to buffer 1 and key=8 records hashing to buffer 0. Buffer 3 is unused.

Consider processing the following SQL projection query:

select distinct title,name from Staff;

You are given the following information:

• the relation Staff has attributes id, name, title, dept, address
• except for id, all are string fields of the same length
• the id attribute is the primary key
• the relation contains 10,000 pages
• there are 10 records per page
• there are 10 memory buffer pages available for sorting

Consider an optimised version of the sorting-based projection algorithm: The initial sorting pass reads the input and creates sorted runs of tuples containing only the attributes name and title. Subsequent merging passes eliminate duplicates while merging the initial runs to obtain a single sorted result (as opposed to doing a separate pass to eliminate duplicates from a sorted result).

1. How many sorted runs are produced on the first pass? What is the average length of these runs?

   Answer:

   In the first pass, two things happen: the two relevant fields are projected out of each record, and the resulting records are sorted in groups and written to an output file. Since all fields are the same size, extracting two fields gives records that are half as big as the original records. This means that the result file will have half as many pages as the original file (i.e. 5,000 pages). Since there are B=10 memory buffers, these 5,000 pages can be sorted into groups of 10-pages each. The first pass thus produces N=ceil(b/B)=500 runs of 10 pages each.

2. How many additional passes will be required to compute the final result of the projection query? What is the I/O cost of these additional passes?

   Answer:

   After the first pass produces sorted groups of 10-pages in length, the remaining passes sort the file and then do a scan to remove duplicates. The number of passes for the sorting is ceil(log_B-1N)=3, and on each of these passes the complete file (5,000 pages) is read and written (i.e. 2*5000=10,000 page I/Os). Since duplicates can be easily eliminated in the final merging phase of the sort, we do not require an additional duplicate-elimination pass (as described in the lecture notes). Thus, the process requires a total of 3*2*5000=30,000 I/Os.

3. Suppose that a clustered B+ tree index on title is available. Is this index likely to offer a cheaper alternative to sorting? Would your answer change if the index were unclustered?

   Answer:

   With a clustered B+ tree index, on title, we know that the file is (almost) sorted on title already. However, this won't help us much since there will be many occurrences of a given title value (e.g. Dr. Mr. Ms.) and the names associated with that title may be spread over many pages and completely unsorted. If the index were unclustered, we would get absolutely no help at all from it.

4. Suppose that a clustered B+ tree index on name is available. Is this index likely to offer a cheaper alternative to sorting? Would your answer change if the index were unclustered?

   Answer:

   Having a clustered index on name means that the file is sorted by name, and thus multiple occurrences of a name are likely to occur in the same data block (or, at worst, adjacent data blocks). A scan of the B+ tree would allow us to establish this and complete the projection with just one pass over the data file. If the index were unclustered, we would get no help from it.

5. Suppose that a clustered B+ tree index on (name,title) is available. Is this index likely to offer a cheaper alternative to sorting? Would your answer change if the index were unclustered?

   Answer:

   Using a clustered B+ tree index on (name,title) would also be more cost-effective than sorting. In this case, even an unclustered B+ tree would be helpful, because we could use an index-only scan to extract the required information from the (already sorted how we want) index file.