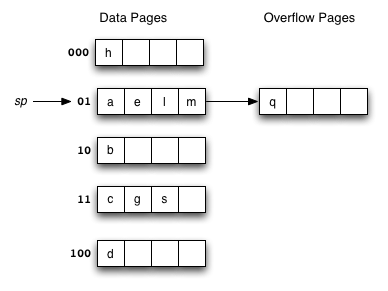
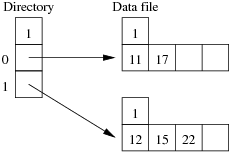
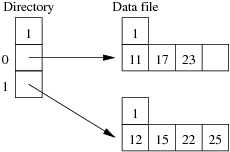
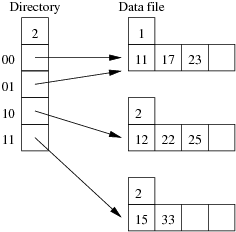
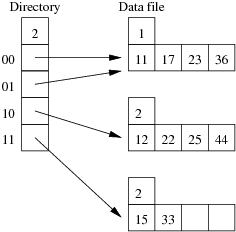
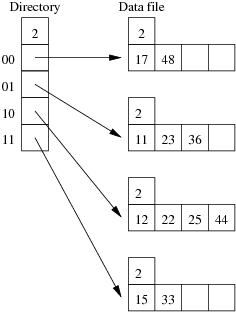
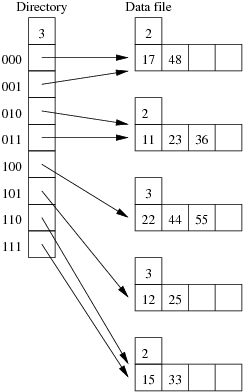
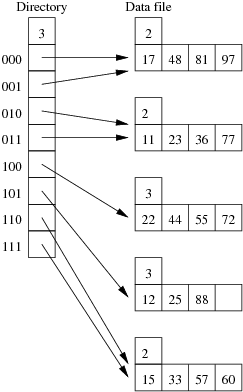
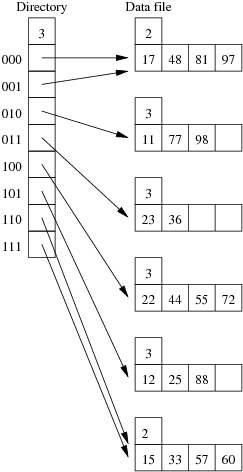
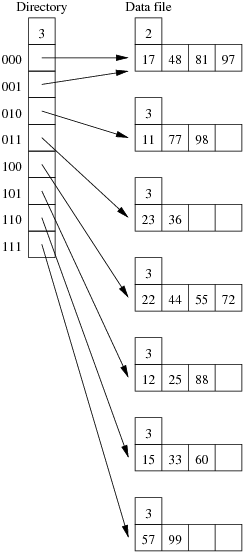
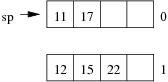
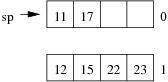
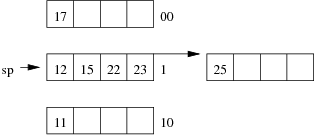
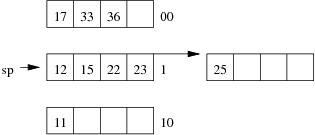
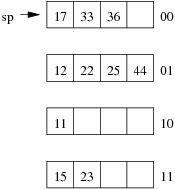
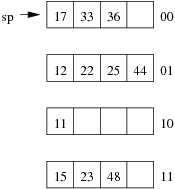
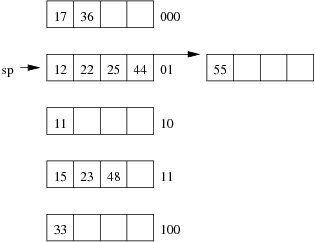
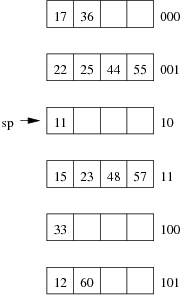
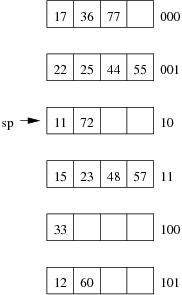
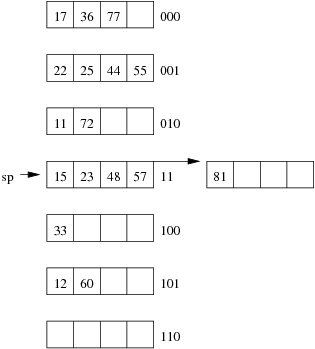
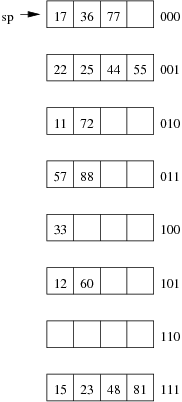
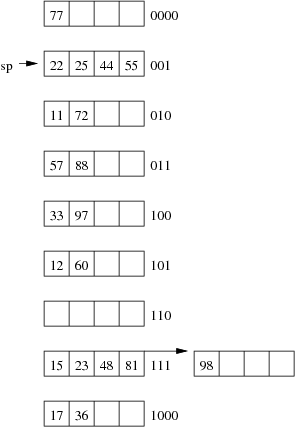
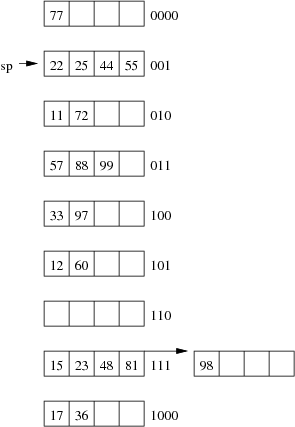
Consider the following example file organisation using extendible hashing. Records are inserted into the file based on single letter keys (only the keys are shown in the diagram).
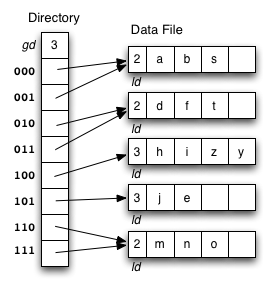
The dictionary contains a "global depth" value (gd), which indicates how many hash bits are being considered in locating data pages via the dictionary. In this example, the depth gd=3 and so the dictionary is size 2gd=2d=8.
Each data page is marked with a "local depth" value (ld), which
indicates the effective number of bits that have been used to place
records in that page. The first data page, for example, has ld=2,
which tells us that only the first two bits of the hash value were used
to place records there (and these two bits were 00).
The third data page, on the other hand, has ld=3, so we know that
all records in that page have their first three hash bits as 100.
Using the above example to clarify, answer the following questions about extendible hashing:
-
Under what circumstances must we double the size of the directory, when we add a new data page?
The directory has to be doubled whenever we split a page that has only one dictionary entry pointing to it. We can detect this condition via the test gd = ld. xxAAxx );?> -
Under what circumstances can we add a new data page without doubling the size of the directory?
We don't need to double the directory if the page to be split has multiple pointers leading to it. We simply make half of those pointers point to the old page, while the other half point to the new page. We can detect this condition via the test ld < gd. xxAAxx );?> - After an insertion that causes the directory size to double, how many data pages have exactly one directory entry pointing to them? Two. The old page that filled up and the new page that was just created. Since we just doubled the number of pointers in the dictionary and added only one new page, all other data pages now have two pointers leading to them. xxAAxx );?>
- Under what circumstances would we need overflow pages in an extendible hashing file? If we had more than Cr records with the same key value. These keys would all have exactly the same hash value, no matter how many bits we take into account, so if we kept doubling the dictionary in the hope of eventually distinguishing them by using more and more bits, then the dictionary would grow without bound. xxAAxx );?>
-
What are the best-case and worst-case scenarios for space
utilisation in the dictionary and the data pages (assuming that
there are no overflow pages)? Under what circumstances do these
scenarios occur?
The best case scenario is when the hash function spreads the
records uniformly among the pages and all pages are full.
We then have 100% space utilisation in the data pages.
Under the best-case scenario, each data page would have
exactly one dictionary entry referring to it
(i.e. gd == ld for every page).
The worst case scenario is when we have an extremely skew hash function (e.g. the hash function maps every key value to the same page address ... at least in the first few hash bits). Let's assume that we fill up the first page and then add one more record. If we needed to consider all 32 bits of the hash before we could find one record that mapped to a different page (e.g. all records have hash value
xxAAxx );?>0000...0000except for one record that has hash value0000...0001, then we would have a dictionary with 232 entries (which is extremely large). At this point, the data page space utilisation would be just over 50% (we have two pages, one of which is full and the other of which contains one record). It is unlikely that an extendible hashing scheme would allow the dictionary to grow this large before giving up on the idea of splitting and resorting to overflow pages instead.