Q2 (15 marks)

$k$-core based structural diversity

Task Overview

Structural diversity is a crucial aspect of graph analysis, providing insights into the connectivity and importance of nodes within a network. Traditional structural diversity measures often focus on the number of components a node connects to, but they can be limited in their ability to capture the full complexity of graph structures. To enhance this analysis, we introduce $k$-core based structural diversity, which combines the concept of $k$-cores with structural diversity to provide a more nuanced understanding of node importance. In this project, you will implement an online efficient algorithm for $k$-core-based structural diversity, allowing for a deeper exploration of graph structures and their implications.

Problem Definition

Definition (Graph)

A simple, undirected, unweighted graph is a pair $G = (V,E)$ where $V$ is the vertex set and $E \subseteq \{\{u,v\}\mid u,v \in V,\;u \ne v\}$ is the edge set. We use $G[V']$ to denote the subgraph of $G$ induced by a subset $V' \subseteq V$.

Definition ($k$-core)

For an integer $k \ge 0$, the $k$-core of a graph $G$, denoted $k(G)$, is the maximal connected induced subgraph $H = (V_H,E_H)$ that satisfies \[ \deg_H(v) \;\ge\; k \quad \text{for every } v \in V_H. \]

Definition (Neighbour-induced subgraph)

For a vertex $v \in V$, its set of neighbours is $N(v) = \{u \in V \mid \{u,v\} \in E\}.$ The subgraph induced by $N(v)$ is called the neighbour-induced subgraph of $v$ and is denoted $\operatorname{nbr}_v = G[N(v)].$

Definition ($k$-core-based Structural Diversity)

Let $\mathcal{K}_k(H)$ denote the $k$-cores of a graph $H$. The $k$-core-based structural diversity of a vertex $v$ is the number of $k$-cores in its neighbour-induced subgraph, denoted as $\tau_k(v)$, which is defined as \[ \tau_k(v) = \bigl| \mathcal{K}_k\bigl( \operatorname{nbr}_v \bigr) \bigr|. \]

Problem Statement

Given a graph $G=(V,E)$ and an integer $k \ge 0$, compute $\tau_k(v)$ for every $v \in V$. The output is an array of length $|V|$ storing, for each vertex, its $k$-core-based structural diversity value. You can assume that the vertex IDs in the graph are consecutive integers starting from 0 to $|V|-1$.

Example

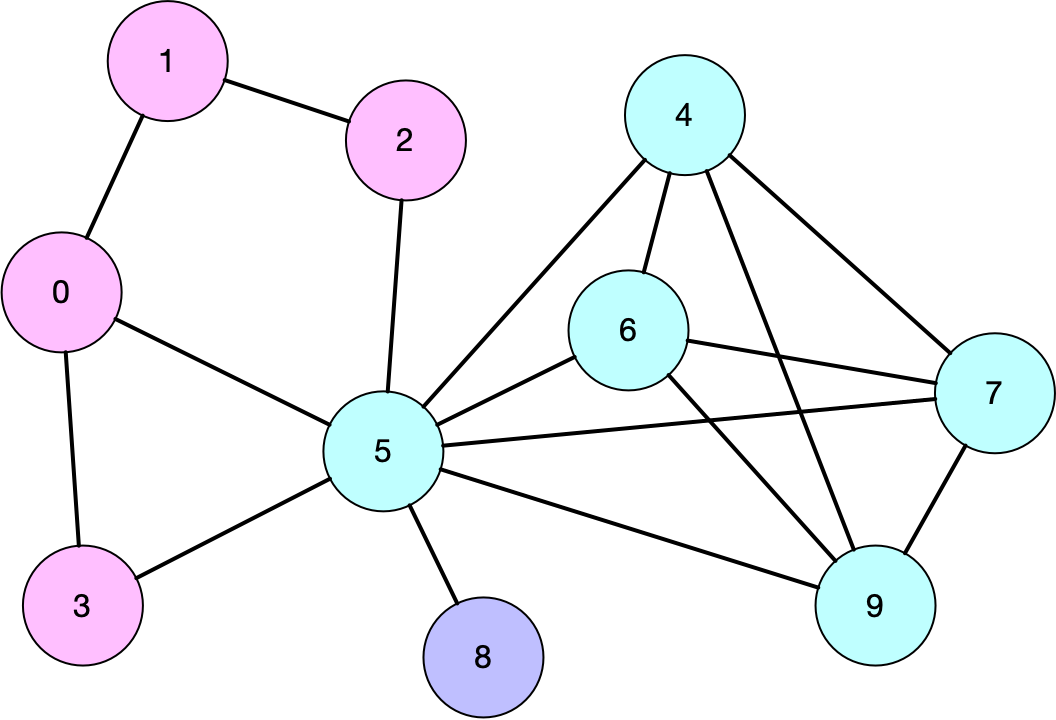
Consider the graph in Figure 1. For vertex 5 we have the neighbour set \[ N(5) = \{0,2,3,4,6,7,8,9\}. \]

$k = 0$
- $\tau_0(5) = 4$
- $\mathcal{K}_0(\operatorname{nbr}_5) = [\{2\}, \{8\}, \{0,3\}, \{4,6,7,9\}]$
$k = 1$
- $\tau_1(5) = 2$
- $\mathcal{K}_1(\operatorname{nbr}_5) = [\{0,3\}, \{4,6,7,9\}]$
$k = 2$
- $\tau_2(5) = 1$
- $\mathcal{K}_2(\operatorname{nbr}_5) = [\{4,6,7,9\}]$
$k = 4$
- $\tau_4(5) = 0$ (no 4-core)

Doing this Project

Open the code template file Q2.ipynb and make a copy in your own Google Drive. You need to implement a class named kCoreBaseStructuralDiversity with a function process(G, k).

We will extract your kCoreBaseStructuralDiversity class (along with any necessary import statements) and test it independently. Your implementation must run correctly without modification in the Colab environment.


class kCoreBaseStructuralDiversity(object):
    def __init__(self):
        pass

    @staticmethod
    def process(G, k):
        """
        Parameters
        ----------
        G : UndirectedUnweightedGraph
        k : int
        Returns
        -------
        List[int]  # τ_k(v) for all v
        """
        # TODO
        τ = [0] * G.vertex_num
        return τ

Required Files

Compress all related files for Q2 (Q2.ipynb and Q2.pdf, which contains your explanation) into Q2.zip, and submit it on Moodle.

Other Marking Criteria

A correct and efficient implementation of an online algorithm with proper documentation will receive full marks.
Partial marks will be awarded for implementations that pass only a subset of the hidden test cases.
Submissions must return Structural diversity values for all vertices in the graph.
You must provide a clear explanation of your algorithm and its time complexity.

Notes

Do not change the input/output format of the provided class or method.
We will test your submission on larger graphs than those shown in the examples.
Make sure to handle edge cases, such as graphs with no edges or isolated vertices.
You can not import any external libraries or modules other than the Python Standard Library.