Q1 (10 marks)

Design a solution to compute the top-k shortest simple paths between two vertices in a large directed weighted graph.

Problem Statement

In this question, you need to design an online algorithm to return the top-k shortest simple (loopless) paths between a given pair of vertices s and t in a large directed weighted graph. Your implementation should return k distinct paths ordered by increasing total path weight.

In other words, any simple path from s to t that is not included in the top-k result must either have a greater total weight than the k-th returned path, or have the same weight but a later lexicographical order.

Background & Marking Criteria

You are expected to implement an online algorithm that returns the top-k shortest simple paths between two vertices in a directed weighted graph. Each returned path must be:

• Simple — acyclic, with no repeated vertices
• Distinct — no duplicate paths

You should aim to design an efficient solution that works on moderately large graphs. In addition to the implementation, a correct time complexity analysis is compulsory and will be marked.

Marks will be awarded based on:

• Correctness (autotests): number of test cases passed
• Theoretical analysis: clarity and correctness of your algorithm description and time complexity

If your code is incomplete or fails some cases, you may still receive partial marks for a clear and well-reasoned explanation. Include your explanation in Q1.pdf, covering your algorithm design, time complexity, and any assumptions or limitations.

Example

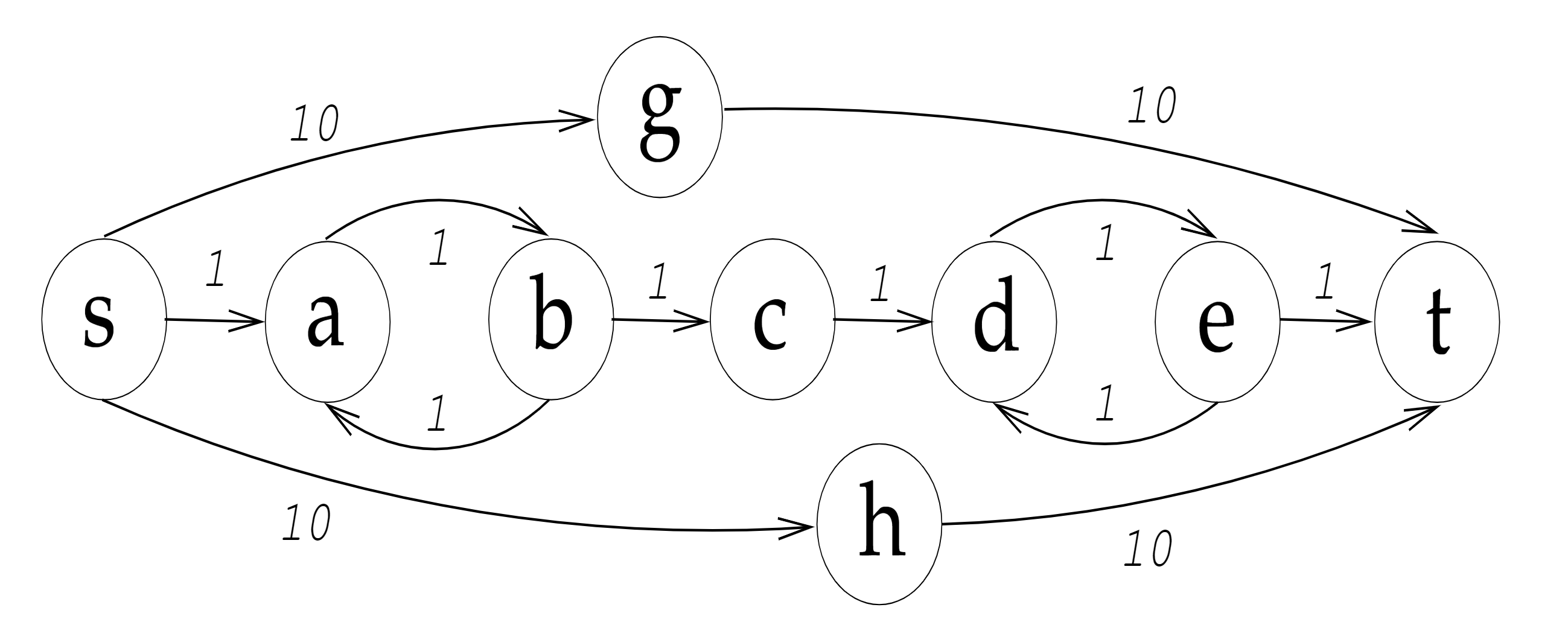
Consider the graph shown in Figure 1. Given source vertex s and target vertex t, the top-k shortest simple paths are:

• k = 1: [[s, a, b, c, d, e, t]]
• k = 2: [[s, a, b, c, d, e, t], [s, g, t]]
• k = 3: [[s, a, b, c, d, e, t], [s, g, t], [s, h, t]]
• k = 4: [[s, a, b, c, d, e, t], [s, g, t], [s, h, t]]

Doing this Project

Open the code template file Q1.ipynb and make a copy in your own Google Drive. You need to implement a class named KShortestPathsQuery with a function query(s, t, k).

We will extract your KShortestPathsQuery class (along with any necessary import statements) and test it independently. Your implementation must run correctly without modification in the Colab environment.

################################################################################
# You can import any Python Standard Library modules.
################################################################################

class KShortestPathsQuery(object):
    def __init__(self):
        pass

    @staticmethod
    def query(G, s, t, k):
        ################################################################################
        # Input:
        #   s: source vertex
        #   t: target vertex
        #   k: number of shortest simple paths to return
        #
        # Output:
        #   A list of top-k shortest simple paths, each as a list of vertex IDs from s to t.
        #
        # Note:
        #   Each path must be simple (no repeated vertices) and distinct.
        #   Paths should be returned in ascending order of total weight.
        #   If multiple paths have the same weight, break ties by lexicographical order.
        #
        # Please analyze the time complexity of your solution.
        ################################################################################
        return []

Required Files

Compress all related files for Q1 (Q1.ipynb and Q1.pdf, which contains your explanation) into Q1.zip, and submit it on Moodle.

Other Marking Criteria

1. A correct and efficient implementation of an online algorithm with proper documentation will receive full marks.
2. Partial marks will be awarded for implementations that pass only a subset of the hidden test cases.
3. Submissions must return simple paths. Paths containing cycles or repeated vertices will be considered incorrect.
4. You must provide a clear explanation of your algorithm and its time complexity.

Notes

1. Your algorithm should handle edge cases such as unreachable targets and cases where fewer than k valid paths exist.
2. Do not change the input/output format of the provided class or method.
3. We will test your submission on larger graphs than those shown in the examples.
4. If multiple simple paths have the same total distance, break ties by lexicographical order of vertex IDs in the path. For example, prefer path 1→2→5 over 1→3→5.
5. You can not import any external libraries or modules other than the Python Standard Library.