|
Week 4 Problem Set Graph Data Structures and Graph Search |

|
|
Week 4 Problem Set Graph Data Structures and Graph Search |

|
For the graph
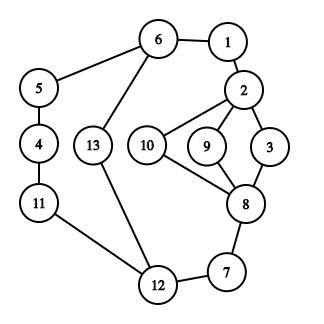
give examples of the smallest (but not of size/length 0) and largest of each of the following:
Answer:
Write pseudocode for computing
of an undirected graph g with n vertices.
Your methods should be representation-independent; the only function you should use is to check if two vertices v,w∈{0,…n-1} are adjacent in g.
The density is the fraction of edges present over all possible edges, which, for an undirected graph with `|E|` edges and `|V|` vertices, is defined as `(2|E|)/(|V|(|V|-1))`.
Determine the asymptotic complexity of your three algorithms. Assume that the adjacency check is performed in constant time, O(1).
Implement your algorithms in a program graphAnalyser.c that
Your program should use the Graph ADT from the lecture (Graph.h and Graph.c). These files should not be changed.
Hint: You may assume that the graph has a maximum of 1000 nodes.
We have also provided a Makefile to simplify the compilation process. Place it in the same directory as your code and simply execute:
make
If you'd like to delete the object files it creates, you can instead execute:
make clean
An example of the program executing is shown below for the graph
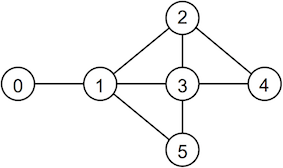
./graphAnalyser Enter the number of vertices: 6 Enter an edge (from): 0 Enter an edge (to): 1 Enter an edge (from): 1 Enter an edge (to): 2 Enter an edge (from): 4 Enter an edge (to): 2 Enter an edge (from): 1 Enter an edge (to): 3 Enter an edge (from): 3 Enter an edge (to): 4 Enter an edge (from): 1 Enter an edge (to): 5 Enter an edge (from): 5 Enter an edge (to): 3 Enter an edge (from): 2 Enter an edge (to): 3 Enter an edge (from): done Done. Vertex degrees: 1, 4, 3, 4, 2, 2 Triplets: 1-2-3 1-3-5 2-3-4 Density: 0.533
Note that any non-numeric data can be used to 'finish' the interaction.
We have created a script that can automatically test your program. To run this test you can execute the dryrun program that corresponds to this exercise. It expects to find a program named graphAnalyser.c in the current directory. You can use dryrun as follows:
9024 dryrun graphAnalyser
Please ensure that your program output follows exactly the format shown in the sample interaction above. In particular, the degree should be shown for the vertices in ascending order, the 3-cliques should be printed in ascending order, and the density should be printed to three decimal places.
Answer:
The following algorithm uses two nested loops to compute the degree of each vertex. Hence its asymptotic running time is O(n2).
degrees(g):
Input graph g
Output array of vertex degrees
for all vertices v∈g do
deg[v]=0
for all vertices w∈g, v≠w do
if v,w adjacent in g then
deg[v]=deg[v]+1
end if
end for
end for
return deg
The following algorithm uses three nested loops to print all 3-cliques in order. Hence its asymptotic running time is O(n3).
show3Cliques(g):
Input graph g of n vertices numbered 0..n-1
for all i=0..n-3 do
for all j=i+1..n-2 do
if i,j adjacent in g then
for all k=j+1..n-1 do
if i,k adjacent in g and j,k adjacent in g then
print i"-"j"-"k
end if
end for
end if
end for
end for
The following algorithm uses two nested loops to calculate the graph density. Hence its asymptotic running time is O(n2).
density(g):
Input graph g
Output graph density
m=0
for all vertices v∈g do
for all vertices w∈g, w>v do
if v,w adjacent in g then
m=m+1
end if
end for
end for
return (2*m)/(n*(n-1))
Sample graphAnalyser.c:
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "Graph.h"
#define MAX_NODES 1000
// determine and output the sequence of vertex degrees
void degrees(Graph g) {
int nV = numOfVertices(g);
int v, w, degree;
printf("Vertex degrees:\n");
for (v = 0; v < nV; v++) {
degree = 0;
for (w = 0; w < nV; w++) {
if (adjacent(g,v,w)) {
degree++;
}
}
printf("%d", degree);
if (v < nV-1) {
printf(", ");
} else {
printf("\n");
}
}
}
// show all 3-cliques of graph g
void show3Cliques(Graph g) {
int i, j, k;
int nV = numOfVertices(g);
printf("Triplets:\n");
for (i = 0; i < nV-2; i++) {
for (j = i+1; j < nV-1; j++) {
if (adjacent(g,i,j)) {
for (k = j+1; k < nV; k++) {
if (adjacent(g,i,k) && adjacent(g,j,k)) {
printf("%d-%d-%d\n", i, j, k);
}
}
}
}
}
}
// calculate and output the density of undirected graph g
void density(Graph g) {
int nV = numOfVertices(g);
int nE = 0;
int v, w;
double density;
for (v = 0; v < nV-1; v++) {
for (w = v+1; w < nV; w++) {
if (adjacent(g,v,w)) {
nE++;
}
}
}
density = (2.0 * (double)nE) / ((double)nV * ((double)nV - 1.0));
printf("Density: %.3lf\n", density);
}
int main(void) {
Edge e;
int nV;
printf("Enter the number of vertices: ");
scanf("%d", &nV);
Graph g = newGraph(nV);
printf("Enter an edge (from): ");
while (scanf("%d", &e.v) == 1) {
printf("Enter an edge (to): ");
scanf("%d", &e.w);
insertEdge(g, e);
printf("Enter an edge (from): ");
}
printf("Done.\n");
degrees(g);
show3Cliques(g);
density(g);
freeGraph(g);
return 0;
}
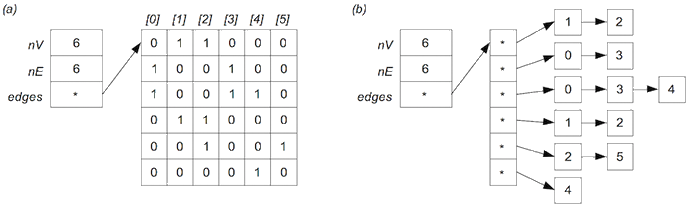
Show how the following graph would be represented by
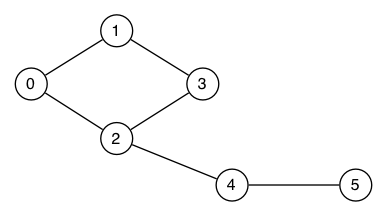
Consider the adjacency matrix and adjacency list representations for graphs. Analyse the storage costs for the two representations in more detail in terms of the number of vertices V and the number of edges E. Determine the E:V ratio at which it is more storage efficient to use an adjacency matrix representation vs the adjacency list representation.
Assumptions. For the purposes of the analysis, ignore the cost of storing the GraphRep structure. Assume that: each pointer is 8 bytes long, a Vertex value is 4 bytes, a linked-list node is 16 bytes long, the adjacency matrix is a complete V×V matrix. Assume also that each adjacency matrix element is 1 byte long. (Hint: Defining the matrix elements as 1-byte boolean values rather than 4-byte integers is a simple way to improve the space efficiency for the adjacency matrix representation.)
The standard adjacency matrix representation for a graph uses a full V×V matrix and stores each edge twice (at [v,w] and [w,v]). This consumes a lot of space, and wastes a lot of space when the graph is sparse. One way to use less space is to store just the upper (or lower) triangular part of the matrix, as shown in the diagram below:
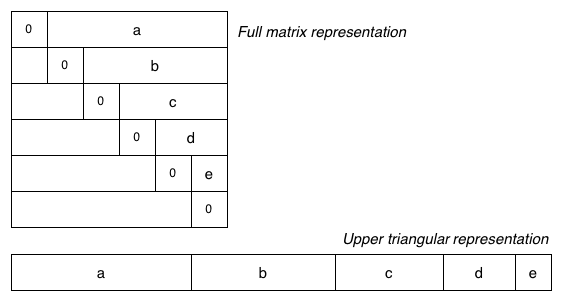
The V×V matrix has been replaced by a single 1-dimensional array g.edges[] containing just the "useful" parts of the matrix.
Accessing the elements is no longer as simple as g.edges[v][w]. Write pseudocode for a method to check whether two vertices v and w are adjacent under the upper-triangle matrix representation of a graph g.
Answer:
The adjacency matrix representation always requires a V×V matrix, regardless of the number of edges, where each element is 1 byte long. It also requires an array of V pointers. This gives a fixed size of V·8+V2 bytes.
The adjacency list representation requires an array of V pointers (the start of each list), with each being 8 bytes long, and then one list node for each edge in each list. The total number of edge nodes is 2E (each edge (v,w) is stored twice, once in the list for v and once in the list for w). Since each node requires 16 bytes (vertex+padding+pointer), this gives a size of V·8+16·2·E. The total storage is thus V·8+32·E.
Since both representations involve V pointers, the difference is based on V2 vs 32E. So, if 32E < V2 (or, equivalently, E:V < V/32), then the adjacency list representation will be more storage-efficient. Conversely, if E:V > V/32, then the adjacency matrix representation will be more storage-efficient.
To pick a concrete example, if V=60 and if we have 112 or fewer edges (112/60 = 1.867 < 60/32 = 1.875), then the adjacency list will be more storage-efficient, otherwise the adjacency matrix will be more storage-efficient.
adjacent(g,v,w):
Input graph g in upper-triangle matrix representation
v, w vertices such that v≠w
Output true if v and w adjacent in g, false otherwise
if v>w then
swap v and w // to ensure v<w
end if
chunksize=g.nV-1, offset=0
for all i=0..v-1 do
offset=offset+chunksize
chunksize=chunksize-1
end for
offset=offset+w-v-1
if g.edges[offset]=0 then return false
else return true
end if
Alternatively, you can compute the overall offset directly via the formula `(nV-1)+(nV-2)+...+(nV-v)+(w-v-1)=v/2(2*nV-v-1)+(w-v-1)` (assuming that v < w).
Both DFS and BFS can be used for a complete search without a specific destination, which means traversing a graph until all reachable nodes have been visited. Show the order in which the nodes of the graph depicted below are visited by
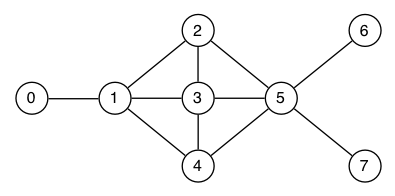
Assume the use of a stack for depth-first search (DFS) and a queue for breadth-first search (BFS), respectively, and use the pseudocode from the lecture: DFS, BFS. Show the state of the stack or queue explicitly in each step. When choosing which neighbour to visit next, always choose the smallest unvisited neighbour.
Answer:
Current Stack (top at left) - 7 7 5 5 2 3 4 6 2 1 3 3 4 6 1 0 3 4 3 3 4 6 0 3 4 3 3 4 6 3 4 4 3 3 4 6 4 4 3 3 4 6 ... 6 -
Current Stack (top at left) - 4 4 1 3 5 1 0 2 3 3 5 0 2 3 3 5 2 3 5 3 3 5 3 5 5 3 3 5 5 6 7 5 3 3 5 6 7 5 3 3 5 7 5 3 3 5 ... - -
Current Queue (front at left) - 7 7 5 5 2 3 4 6 2 3 4 6 1 3 4 6 1 4 6 1 6 1 1 0 0 -
Current Queue (front at left) - 4 4 1 3 5 1 3 5 0 2 3 5 0 2 5 0 2 6 7 0 2 6 7 2 6 7 6 7 7 -
Take the "buggy" cycle check from the lecture and design a correct algorithm, in pseudocode, to use depth-first search to determine if a graph has a cycle.
Write a C program cycleCheck.c that implements your solution to check whether a graph has a cycle. The graph should be built from user input in the same way as in exercise 2. Your program should use the Graph ADT from the lecture (Graph.h and Graph.c). These files should not be changed.
An example of the program executing is shown below for the following graph:
./cycleCheck Enter the number of vertices: 9 Enter an edge (from): 0 Enter an edge (to): 1 Enter an edge (from): 1 Enter an edge (to): 2 Enter an edge (from): 4 Enter an edge (to): 3 Enter an edge (from): 6 Enter an edge (to): 5 Enter an edge (from): 6 Enter an edge (to): 7 Enter an edge (from): 5 Enter an edge (to): 7 Enter an edge (from): 5 Enter an edge (to): 8 Enter an edge (from): 7 Enter an edge (to): 8 Enter an edge (from): done Done. The graph is cyclic.
If the graph has no cycle, then the output should be:
./cycleCheck Enter the number of vertices: 3 Enter an edge (from): 0 Enter an edge (to): 1 Enter an edge (from): # Done. The graph is cycle-free.
You may assume that a graph has a maximum of 1000 nodes.
To test your program you can execute the dryrun program that corresponds to this exercise. It expects to find a program named cycleCheck.c in the current directory. You can use dryrun as follows:
9024 dryrun cycleCheck
Note: Please ensure that your output follows exactly the format shown above.
Answer:
hasCycle(G): | Input graph G | Output true if G has a cycle, false otherwise | | mark all vertices as unvisited | for each vertex v∈G do // make sure to check all connected components | | if v has not been visited then | | if dfsCycleCheck(G,v,v) then | | return true | | end if | | end if | end for | return false dfsCycleCheck(G,v,u): // look for a cycle that does not go back directly to u | mark v as visited | for each (v,w)∈edges(G) do | | if w has not been visited then | | | if dfsCycleCheck(G,w,v) then | | | return true | | | end if | | else if w≠u then | | | return true | | end if | end for | return false
The following two C functions implement this algorithm:
#define MAX_NODES 1000
int visited[MAX_NODES];
bool dfsCycleCheck(Graph g, Vertex v, Vertex u) {
visited[v] = true;
Vertex w;
for (w = 0; w < numOfVertices(g); w++) {
if (adjacent(g, v, w)) {
if (!visited[w]) {
if (dfsCycleCheck(g, w, v))
return true;
} else if (w != u) {
return true;
}
}
}
return false;
}
bool hasCycle(Graph g) {
int v, nV = numOfVertices(g);
for (v = 0; v < nV; v++)
visited[v] = false;
for (v = 0; v < nV; v++)
if (!visited[v])
if (dfsCycleCheck(g, v, v))
return true;
return false;
}
Computing connected components can be avoided by maintaining a vertex-indexed connected components array as part of the Graph representation structure:
typedef struct GraphRep *Graph;
struct GraphRep {
...
int nC; // # connected components
int *cc; /* which component each vertex is contained in
i.e. array [0..nV-1] of 0..nC-1 */
...
}
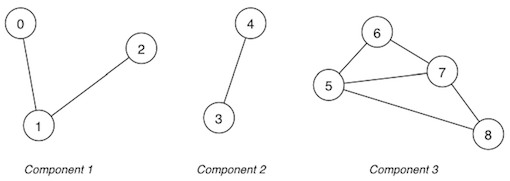
Consider the following graph with multiple components:
Assume a vertex-indexed connected components array cc[0..nV-1] as introduced above:
nC = 2
cc[] = {0,0,0,1,1,1,0,0,0,1}
Show how the cc[] array would change if
Consider an adjacency matrix graph representation augmented by the two fields
newGraph(V): | Input number of nodes V | Output new empty graph | | g.nV=V, g.nE=0, g.nC=V | allocate memory for g.cc[] | allocate memory for g.edges[][] | for all i=0..V-1 do | g.cc[i]=i | for all j=0..V-1 do | g.edges[i][j]=0 | end for | end for | return g
Modify the pseudocode for edge insertion and edge removal from the lecture to maintain the two new fields.
Hints:
Inserting an edge may reduce the number of connected components. If two components are merged, then the new component should adopt whichever ID is lesser of the two. Meanwhile the component with the largest ID should be re-assigned the greater of the two. This is to ensure the ID space remains contiguous from 0.
Removing an edge may increase the number of connected components. For such an edge (v, w), vertex v and all nodes reachable from it should be assigned the next available component ID, while w and all nodes reachable from it retain their original component ID.
Download the Graph ADT from the lecture (Graph.h and Graph.c), rename them as GraphCC.h and GraphCC.c, and implement the above changes. You will also need to update the reference to Graph.h within GraphCC.c.
Write a function in GraphCC.c that prints out the connected components array. You can see the expected output format in the sample output at the end of this exercise. The function signature is below, which you will also need to add as a prototype in GraphCC.h:
void showComponents(Graph)
A program connectedComponents.c is provided to drive your modified Graph ADT. It builds a graph from user input by:
Copy the Makefile from Exercise 2 and modify it to compile GraphCC.c and connectedComponents.c. Its target should be an executable named connectedComponents.
An example of the program executing is shown below for the graph in Exercise 2 where edges 1-2, 1-3, and 1-5 have subsequently been removed:
./connectedComponents Enter the number of vertices: 6 [i]nsert or [r]emove an edge: i 0 1 [i]nsert or [r]emove an edge: i 1 2 [i]nsert or [r]emove an edge: i 4 2 [i]nsert or [r]emove an edge: i 1 3 [i]nsert or [r]emove an edge: i 3 4 [i]nsert or [r]emove an edge: i 1 5 [i]nsert or [r]emove an edge: i 5 3 [i]nsert or [r]emove an edge: i 2 3 [i]nsert or [r]emove an edge: r 1 2 [i]nsert or [r]emove an edge: r 1 3 [i]nsert or [r]emove an edge: r 1 5 [i]nsert or [r]emove an edge: done Connected components: 1, 1, 0, 0, 0, 0We have created a script that can automatically test your program. To run this test you can execute the dryrun program that corresponds to this exercise. It expects to find your modified
9024 dryrun connectedComponents
Note: Please ensure that your output follows exactly the format shown above.
Answer:
After removing d, cc[] = {0,0,0,1,1,1,0,0,0,1} (i.e. unchanged)
After removing b, cc[] = {0,0,2,1,1,1,2,0,2,1} with nC=3
insertEdge(g,(v,w)):
| Input graph g, edge (v,w)
|
| if g.edges[v][w]=0 then // (v,w) not in graph
| | g.edges[v][w]=1, g.edges[w][v]=1 // set to true
| | g.nE=g.nE+1
| | if g.cc[v]≠g.cc[w] then // v,w in different components?
| | | c=min{g.cc[v],g.cc[w]} // ⇒ merge components c and d
| | | d=max{g.cc[v],g.cc[w]}
| | | for all vertices v∈g do
| | | if g.cc[v]=d then
| | | g.cc[v]=c // move node from component d to c
| | | else if g.cc[v]=g.nC-1 then
| | | g.cc[v]=d // replace largest component ID by d
| | | end if
| | | end for
| | | g.nC=g.nC-1
| | end if
| end if
Removing an edge may increase the number of connected components:
removeEdge(g,(v,w)): | Input graph g, edge (v,w) | | if g.edges[v][w]≠0 then // (v,w) in graph | | g.edges[v][w]=0, g.edges[w][v]=0 // set to false | | if not hasPath(g,v,w) then // v,w no longer connected? | | dfsNewComponent(g,v,g.nC) // ⇒ put v + connected vertices into new component | | g.nC=g.nC+1 | | end if | end if dfsNewComponent(g,v,componentID): | Input graph g, vertex v, new componentID for v and connected vertices | | g.cc[v]=componentID | for all vertices w adjacent to v do | if g.cc[w]≠componentID then | dfsNewComponent(g,w,componentID) | end if | end if
// Graph ADT interface
#include <stdbool.h>
typedef struct GraphRep *Graph;
// vertices are ints
typedef int Vertex;
// edges are pairs of vertices (end-points)
typedef struct Edge {
Vertex v;
Vertex w;
} Edge;
Graph newGraph(int);
int numOfVertices(Graph);
void insertEdge(Graph, Edge);
void removeEdge(Graph, Edge);
bool adjacent(Graph, Vertex, Vertex);
void showGraph(Graph);
void showComponents(Graph);
void freeGraph(Graph);
Sample GraphCC.c:
// Graph ADT
// Adjacency Matrix Representation
#include "GraphCC.h"
#include <assert.h>
#include <stdlib.h>
#include <stdio.h>
#include <stdbool.h>
typedef struct GraphRep {
int **edges; // adjacency matrix
int nV; // #vertices
int nE; // #edges
int nC; // #connected components
int *cc; /* which component each vertex is contained in
i.e. array [0..nV-1] of 0..nC-1 */
bool *visited; // to track exploration during path check
} GraphRep;
Graph newGraph(int V) {
assert(V >= 0);
int i;
Graph g = malloc(sizeof(GraphRep));
assert(g != NULL);
g->nV = V;
g->nE = 0;
g->nC = V;
// allocate memory for connected components array
g->cc = malloc(V * sizeof(int));
assert(g->cc != NULL);
// allocate memory for visited array
g->visited = malloc(V * sizeof(bool));
assert(g->visited != NULL);
// allocate memory for each row
g->edges = malloc(V * sizeof(int *));
assert(g->edges != NULL);
// allocate memory for each column and initialise with 0
for (i = 0; i < V; i++) {
g->cc[i] = i;
g->edges[i] = calloc(V, sizeof(int));
assert(g->edges[i] != NULL);
}
return g;
}
int numOfVertices(Graph g) {
return g->nV;
}
// check if vertex is valid in a graph
bool validV(Graph g, Vertex v) {
return (g != NULL && v >= 0 && v < g->nV);
}
void insertEdge(Graph g, Edge e) {
assert(g != NULL && validV(g,e.v) && validV(g,e.w));
int c, d, i;
if (!g->edges[e.v][e.w]) { // edge e not in graph
g->edges[e.v][e.w] = 1;
g->edges[e.w][e.v] = 1;
g->nE++;
if (g->cc[e.v] != g->cc[e.w]) { // v,w in different components?
if (g->cc[e.v] < g->cc[e.w]) { // ⇒ merge components c and d
c = g->cc[e.v];
d = g->cc[e.w];
} else {
c = g->cc[e.w];
d = g->cc[e.v];
}
for (i = 0; i < g->nV; i++) {
if (g->cc[i] == d) {
g->cc[i] = c; // move node from component d to c
} else if (g->cc[i] == g->nC - 1) {
g->cc[i] = d; // replace largest component ID by d
}
}
g->nC--;
}
}
}
bool dfsPathCheck(Graph g, Vertex v, Vertex dest) {
assert(g != NULL);
Vertex w;
g->visited[v] = true;
if (v == dest) {
return true;
} else {
for (w = 0; w < numOfVertices(g); w++) {
if (adjacent(g, v, w) && !g->visited[w]) {
if (dfsPathCheck(g, w, dest)) {
return true;
}
}
}
}
return false;
}
bool hasPath(Graph g, Vertex src, Vertex dest) {
assert(g != NULL);
Vertex v;
for (v = 0; v < numOfVertices(g); v++) {
g->visited[v] = false;
}
return dfsPathCheck(g, src, dest);
}
void dfsNewComponent(Graph g, Vertex v, int componentID) {
Vertex w;
g->cc[v] = componentID;
for (w = 0; w < numOfVertices(g); w++) {
if (adjacent(g, v, w)) {
if (g->cc[w] != componentID) {
dfsNewComponent(g, w, componentID);
}
}
}
}
void removeEdge(Graph g, Edge e) {
assert(g != NULL && validV(g,e.v) && validV(g,e.w));
if (g->edges[e.v][e.w]) { // edge e in graph
g->edges[e.v][e.w] = 0; // set to false
g->edges[e.w][e.v] = 0;
g->nE--;
if (!hasPath(g, e.v, e.w)) {
dfsNewComponent(g, e.v, g->nC);
g->nC++;
}
}
}
bool adjacent(Graph g, Vertex v, Vertex w) {
assert(g != NULL && validV(g,v) && validV(g,w));
return (g->edges[v][w] != 0);
}
void showGraph(Graph g) {
assert(g != NULL);
int i, j;
printf("Number of vertices: %d\n", g->nV);
printf("Number of edges: %d\n", g->nE);
for (i = 0; i < g->nV; i++) {
for (j = i+1; j < g->nV; j++) {
if (g->edges[i][j]) {
printf("Edge %d - %d\n", i, j);
}
}
}
}
void showComponents(Graph g) {
assert(g != NULL);
int i;
printf("Connected components:\n");
for (i = 0; i < g->nV; i++) {
printf("%d", g->cc[i]);
if (i < g->nV-1) {
printf(", ");
} else {
printf("\n");
}
}
}
void freeGraph(Graph g) {
assert(g != NULL);
int i;
for (i = 0; i < g->nV; i++) {
free(g->edges[i]);
}
free(g->edges);
free(g->cc);
free(g->visited);
free(g);
}
CC = gcc CFLAGS = -Wall -Werror -std=c11 .PHONY : clean connectedComponents : connectedComponents.o GraphCC.o $(CC) $(CFLAGS) -o $@ connectedComponents.o GraphCC.c connectedComponents.o : connectedComponents.c GraphCC.h $(CC) $(CFLAGS) -c connectedComponents.c GraphCC.o : GraphCC.c GraphCC.h $(CC) $(CFLAGS) -c GraphCC.c clean : rm -f -- *.o connectedComponents
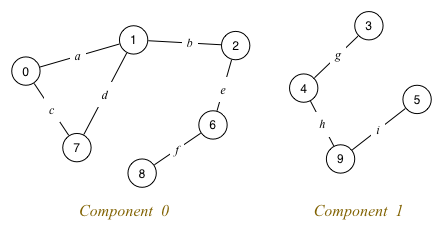
Identify any Hamiltonian/Euler paths/circuits in the following graphs:
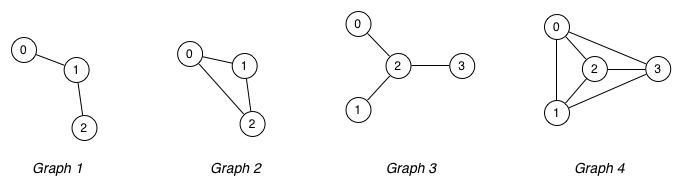
Find an Euler path and an Euler circuit (if they exist) in the following graph:
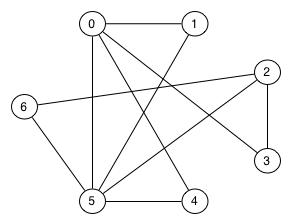
Answer:
Graph 1: has both Euler and Hamiltonian paths (e.g. 0-1-2), but cannot have circuits as there are no cycles.
Graph 2: has both Euler paths (e.g. 0-1-2-0) and Hamiltonian paths (e.g. 0-1-2); also has both Euler and Hamiltonian circuits (e.g. 0-1-2-0).
Graph 3: has neither Euler nor Hamiltonian paths, nor Euler nor Hamiltonian circuits.
Graph 4: has Hamiltonian paths (e.g. 0-1-2-3) and Hamiltonian circuits (e.g. 0-1-2-3-0); it has neither an Euler path nor an Euler circuit.
An Euler path: 2-6-5-2-3-0-1-5-0-4-5
No Euler circuit since two vertices (2 and 5) have odd degree.
Write pseudocode to compute the largest size of a clique in a graph. For example, if the input happens to be the complete graph K5 but with any one edge missing, then the output should be 4. Extend your program from Exercise 2 by an implementation of your algorithm to compute the largest size of a clique in a graph.
Hint: Computing the maximum size of a clique in a graph is known to be an NP-hard problem. Try a generate-and-test strategy.Answer:
As an NP-hard problem, no tractable algorithm for computing the maximum size of a clique in a graph is known. Here is a sample 'brute-force' algorithm that essentially generates-and-tests all possible subsets of vertices to determine the maximum size of a complete subgraph.
maxCliqueSize(g,v,clique,k):
| Input g graph with n nodes 0..n-1
| v next vertex to consider
| clique some subset of nodes 0..v-1 that forms a clique
| k size of that clique
| Output size of largest complete subgraph of g that extends clique with nodes from v..n-1
|
| if v=n then // no more vertices to consider
| return k
| else
| | k1=maxCliqueSize(g,v+1,clique,k) /* find largest complete subgraph that
| | extends clique without considering v */
| | for all w∈clique do // check if v can be added to clique:
| | | if v is not adjacent to w then // if v not adjacent to some node in clique
| | | return k1 // ⇒ return largest clique size without v
| | | end if
| | end for
| | add v to clique
| | k2=maxCliqueSize(g,v+1,clique,k+1) // find largest clique extending clique ∪ {v}
| | if k2>k1 then return k2
| | else return k1
| | end if
| end if
Starting with an empty clique, the function call maxCliqueSize(g,0,clique,0) will return the maximum clique size of graph g.
The following C program implements this algorithm:
int maxCliqueSize(Graph g, int v, int clique[], int k) {
//
// g graph
// v next vertex to consider
// clique[] some subset of nodes 0..v-1 that forms a clique
// k size of that clique
//
// returns size of largest complete subgraph of g that extends clique[] with nodes from v..nV-1
//
if (v == numOfVertices(g)) { // no more vertices to consider
return k;
} else {
int k1 = maxCliqueSize(g, v+1, clique, k); /* find largest complete subgraph that
extends clique[] without considering v */
int i;
for (i = 0; i < k; i++) // check if v can be added to clique[]:
if (!adjacent(g, v, clique[i])) // if v not adjacent to some node in clique[]
return k1; // => return largest clique size without v
clique[k] = v; // add v to clique[]
int k2 = maxCliqueSize(g, v+1, clique, k+1); // find largest clique extending clique[]+v
if (k2 > k1)
return k2;
else
return k1;
}
To call this recursive function on a graph g with nV vertices:
int *clique = malloc(nV * sizeof(int)); // allocate memory for an array of vertices int m = maxCliqueSize(g, 0, clique, 0); // start at vertex 0 with clique of size 0 free(clique);
For the keen: Here you can read more about the computational aspects of computing cliques including some references to more sophisticated algorithms.
After you've solved the exercises, go to COMP9024 23T3 Quiz Week 4 to answer 5 quiz questions on this week's problem set and lecture.
The quiz is worth 2 marks.
There is no time limit on the quiz once you have started it, but the deadline for submitting your quiz answers is Tuesday, 10 October 5:00:00pm.
Please continue to respect the quiz rules:
Do …
Do not …
Reproducing, publishing, posting, distributing or translating this page is an infringement of copyright and will be referred to UNSW Conduct and Integrity for action.