COMP9020 23T1 - Week 5 Problem Set

Week 5 Problem Set
Graphs and Trees

(Warming Up)
1. For the following graph $G$,
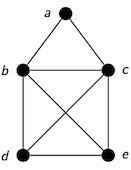
  1. give all simple paths of length 3 starting in b and ending in c;
  2. give the vertex sequence of two different paths between b and c of length 3 that are not simple;
  3. give a cycle of length 4;
  4. give the degree sequence of the graph;
  5. verify that $\sum_{v\in V(G)} \mbox{deg}(v)=2\cdot |E(G)|$ holds (cf. slide 6, week 5).
2. Is the above graph $G$ planar?
3. Draw a complete bipartite K_2,2 graph. Find both an Euler circuit and a Hamiltonian path in your graph and determine their respective length.
4. What is the chromatic number $\chi$ of your graph for Exercise c.? And what is its clique number $\kappa$?
Answer:
1. 1. {b,d}, {d,e}, {e,c} and {b,e}, {e,d}, {d,c}.
  2. b,a,b,c and b,c,d,c. Other solutions are possible.
  3. {a,b}, {b,d}, {d,c}, {c,a} and many other paths.
  4. 0, 0, 1, 2, 2. No vertex has degree 0 or 1. Vertex a is of degree 2. Vertices d and e are of degree 3 while vertices b and c have degree 4.
  5. The graph has one vertex of degree 2, two vertices of degree 3 and two vertices of degree 4. Hence, $\sum_{v\in V(G)} \mbox{deg}(v)=1\cdot 2+2\cdot 3+2\cdot 4=16$. This is twice the number of edges, $|E(G)|=8$.
2. The graph is planar: Redraw one of the edges {b,e} or {c,d} such that it does not intersect with any of the other edges.
3. A K_2,2 graph:
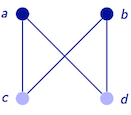
  - All Euler paths are circuits, and they all are of length 4. Example: {a,c}, {c,b}, {b,d}, {d,a}.
  - All Hamiltonian paths are of length 3. Example: {a,c}, {c,b}, {b,d}.
4. $\chi(K_{2,2})=\kappa(K_{2,2})=2$. Two colours are both necessary and sufficient. There are cliques of size 2 (each edge is one such clique) but no "triangles", i.e., 3-cliques.
(Graph properties)
True or false?
1. The complete bipartite graph K_5,5 has no cycle of length five.
2. If you add a new edge to a cycle C₅, the resulting graph will always contain a 3-clique.
3. If you remove two edges from K₅, the resulting graph will always have a clique number of 4.
4. If you remove three edges from graph G in Exercise 1a., the resulting graph will always be acyclic or disconnected.
5. There is a graph with degree sequence 0, 1, 5, 1.
6. There are 3·3 = 9 different automorphisms of K₃.
Answer:
1. True. In general, bipartite graphs can only have cycles of even length. If V₁,V₂ denote the two groups of nodes in the bipartite graph, then every path starting from, say, a node v ∈ V₁ must alternate its vertices between V₁ and V₂. If it is a cycle (that is, eventually returns to node v), it must have an even number of such alternations, in other words, it contains an even number of edges.
2. True. The two newly connected vertices will always form a 3-clique with one of the other vertices.
3. False. Remove any two edges which have no common vertex. In the resulting graph there will be no four fully interconnected vertices; in other words it will not contain K₄, and will have a clique number of 3.
4. False. The resulting graph does not satisfy $|V|=|E|+1$, hence if it is connected then it cannot be a tree and therefore must contain a cycle.
5. True. Take, for example, the graph from the answer to Exercise 6.1.13(a) on slide 9 (week 5) and add a path of length 2 (with 2 new vertices) to one of the four vertices.
6. False. There are 3! = 6 automorphisms of K₃:
  - v₁↦v₁, v₂↦v₂, v₃↦v₃
  - v₁↦v₁, v₂↦v₃, v₃↦v₂
  - v₁↦v₂, v₂↦v₁, v₃↦v₃
  - v₁↦v₂, v₂↦v₃, v₃↦v₁
  - v₁↦v₃, v₂↦v₁, v₃↦v₂
  - v₁↦v₃, v₂↦v₂, v₃↦v₁
(Graph traversal)
For each of the following graphs, show a Hamiltonian path or argue why no such path exists.
1. A connected graph with degree sequence 0,2,2,2 and clique number 3.
2. K_4,3
3. K_1,4,1
4. K_4,2,2
5. All graphs with degree sequence 0, 3, 1, 1.
6. All graphs with degree sequence 0, 0, 6.
Answer:
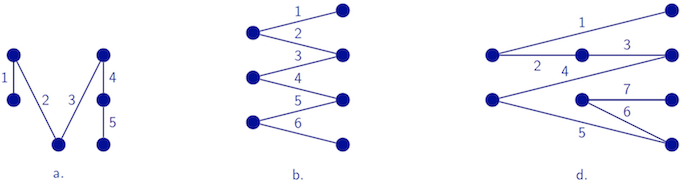
1. True. The only graph that satisfies the specification is the one depicted on slide 18 (week 5). A Hamiltonian path is depicted above.
2. True. A Hamiltonian path is depicted above.
3. False. Even if you start with one of the 4 vertices in the largest partition, you can visit at most 3 of them before you have to return to a previously visited vertex from one of the other two partitions.
4. True. A Hamiltonian path is depicted above.
5. False. The top right tree on slide 17 (week 5) is the only graph on 5 nodes that has one vertex of degree 3, one vertex of degree 2 plus three vertices of degree 1. This tree has no Hamiltonian path since you have to go through the top node at least twice in order to visit all three nodes of degree 1.
6. False. A graph consisting of two disconnected sub-graphs K₃ has degree sequence 0,0,6 but does not contain a Hamiltonian path.
(Graph colouring)
For each of the following graphs G, determine its chromatic number $\chi(G)$. If there are different graphs that satisfy the specification, choose one with the smallest chromatic number.
1. The graph on the left-hand side on slide 39 (week 5).
2. A graph obtained by adding three new edges to C₈.
3. A graph obtained by removing three edges from K_3,3.
4. A graph obtained by removing three edges from K₅.
Answer:
1. The graph has a cycle of length 5, hence 3 colours are necessary. It is possible to find such a 3-colouring, so $\chi(G)=3$.
2. $\chi(C_8)=2$, and you can add three edges so that the resulting graph still satisfies $\chi(G)=2$: For example, connect the 1^st and 4^th node in the cycle, the 2^nd and 5^th node, plus the 3^rd and 6^th node.
3. The remaining graph will still be bipartite, hence $\chi(G)=2$.
4. $\chi(K_5)=5$, but if you remove two edges {v₁,w₁} and {v₂,w₂} with no vertex in common, then v_i and w_i can be coloured the same, for i = 1,2. Hence, 3 colours are sufficient (and necessary).
(Planar graphs)
True or false?
1. All graphs whose clique number is 4 are planar.
2. All graphs whose chromatic number is 2 are planar.
3. All graphs with 5 nodes and 9 edges are planar.
4. You cannot obtain a nonplanar graph by adding 3 edges to a tree.
5. You cannot obtain a nonplanar graph by adding 3 edges to a cycle.
6. You can obtain a planar graph by removing two edges from K₆.
Answer:
1. False. For example, K_3,3 has a clique number of only 2 but is not planar. You can add more edges to turn K_3,3 into a graph whose clique number is 4 (and which, of course, remains nonplanar).
2. False. For example, K_3,3 has a chromatic number of 2 but is not planar.
3. True. For the minimal nonplanar graph K_3,3 you need 6 nodes, and for the other minimal nonplanar graph K₅ you need 10 edges.
4. True. Every tree satisfies $|E|=|V|-1$. Adding 3 edges gives you a graph with $|E|=|V|+2$, but you would need three more edges than vertices for K_3,3, and five more edges than vertices for K₅.
5. False. You can add 3 edges to C₆ (a graph with 6 vertices and 6 edges) in such a way that you obtain the nonplanar K_3,3 (a graph with 6 vertices and 9 edges).
6. False. The remaining graph will always contain K_3,3, which is nonplanar.
(Constructing graphs)
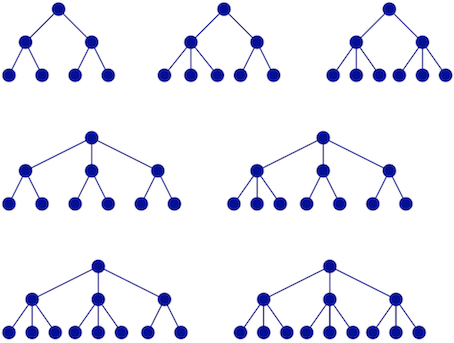
A graph G is a 2-3 tree if:
- G is a rooted tree.
- Each node has either 2 or 3 children (unless it is a leaf node, which has no children).
- All paths from the root to the leaves have the same length.
There are seven different types of 2-3 trees of height 2 (i.e., which are non-isomorphic). Draw one tree of each type.

Answer:
(Mid-term practice test)
To prepare for the mid-term online test on Friday, 24 March, 10:30am, go to COMP9020 23T1 Practice Test to see 3 sample questions.
Note:
- The practice test will automatically close 1 hour + 5 minutes (= 65 minutes) after you have started it, just like the mid-term test will.
- The practice test will end on Thursday, 23 March, 10:00am. It will no longer be available afterwards.
- Your answers to the open questions will not be marked, but you will get to see sample solutions after the practice test has ended on Thursday.
Challenge Exercise
1. What is the minimum number of edges that need to be removed from K₅ so that the resulting graph has a chromatic number of
  - 3 ?
  - 2 ?
  - 1 ?
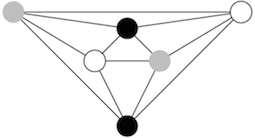
2. Give a planar drawing of K_2,2,2. Can you find one with only straight lines?
Answer:
1. $\chi(K_5)=5$. Minimum number of edges that need to be removed:
  - 2 edges. To achieve $\chi=3$, one needs (at least) to avoid having any 4-cliques. Removing one edge leaves a 4-clique (actually two such cliques — including any one but not both of that edge's endpoints, plus the remaining three vertices). Removing two edges suffices — remove any pair of edges which do not share a common vertex; the remaining graph can then be coloured with 3 colours.
  - 4 edges. A chromatic number of 2 means that the graph is bipartite, with two groups of nodes where each group can be painted with one colour. To minimise the number of removed edges, we want to have as many edges as possible in the remaining bipartite graph. We therefore look at complete bipartite graphs with a total of 5 vertices. As K_1,4 has four edges and K_2,3 has six edges, the latter is the better choice. To reach it we need to remove 4 of the edges in K₅.
  - 10 edges. A chromatic number of 1 means a fully disconnected graph, with no edges at all. Therefore all 10 edges of the original graph must be removed.
2. A planar drawing of K_2,2,2 with straight lines:

Assessment

After you have solved the exercises, go to COMP9020 23T1 Quiz Week 5 to answer 5 quiz questions on this week's problem set (Exercises 2-6 only) and lecture.

The quiz is worth 2 marks.

There is no time limit on the quiz once you have started it, but the deadline for submitting your quiz answers is Tuesday, 21 March 5:00:00pm.

Please continue to respect the quiz rules:

Do …

use your own best judgement to understand & solve a question
discuss quizzes on the forum only after the deadline on Tuesday

Do not …

post specific questions about the quiz before the Tuesday deadline
agonise too much about a question that you find too difficult

Optional additional exercises from the textbook

If you are using the textbook R & W, 5th edition, and want to do additional exercises for practice, I recommend:

6.1.15; 6.1.21(a),(c),(e),(g); 6.2.15(a); 6.3.11(a); 6.7.4(a)–(c) (Supplementary)

All of these have solutions in the textbook.

Reproducing, publishing, posting, distributing or translating this page is an infringement of copyright and will be referred to UNSW Conduct and Integrity for action.