COMP3411 Artificial Intelligence
Session 1, 2014

Week 4 Tutorial - Informed Search and Games

  1. Apply the alpha-beta search algorithm to the following game tree, indicating clearly the values of alpha and beta at each node as the algorithm progresses, and circling the nodes that would not be evaluated.

  2. Consider the following arrangement of tiles in the 8-puzzle:

    123
    85
    476

    Keeping in mind that the goal state is:

    123
    456
    78

    Trace the A*Search algorithm using the Total Manhattan Distance heuristic, to find the shortest path from the initial state shown above, to the goal state.

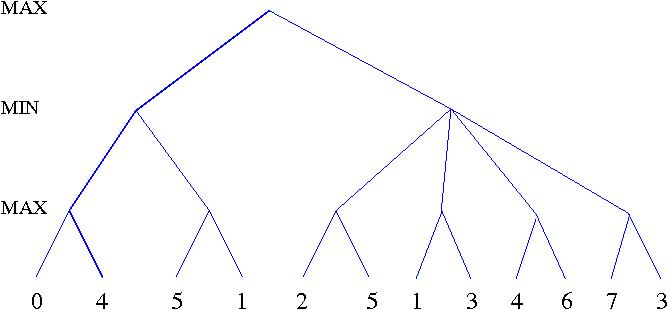
  3. Consider the game of tic-tac-toe (naughts and crosses). If minimax (or alpha-beta) were to search the entire game tree, it would evaluate all opening moves equally - because it assumes the opponent will play optimally, which leads to a draw in the end, no matter what the opening move. However, if we assume the opponent could make an error, we can see that some opening moves are better than others. Explain why.

  4. (5.16) This question considers pruning in games with chance nodes. This figure shows the complete game tree for a very simple such game. Assume that the leaf nodes are to be evaluated in left-to-right order, and that before a leaf node is evaluated, we know nothing about its value -- the range of possible values is -∞ to ∞.

    1. Copy the figure, mark the value of all internal nodes, and indicate the best move at the root with an arrow.
    2. Given the values of the first six leaves, do we need to evaluate the seventh and eighth leaf? Given the values of the first seven leaves, do we need to evaluate the eighth leaf? Explain your answers.
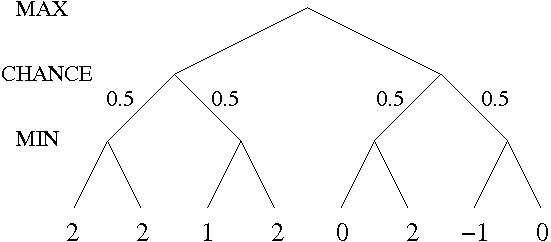
    3. Suppose the leaf node values are known to lie between -2 and 2 inclusive. After the first two leaves are evaluated, what is the value range for the left-hand chance node?
    4. Circle all the leaves that need to be evaluated under the assumption in Part c.

  5. 6.13 (2nd Ed) The Chinook checkers program makes extensive use of endgame databases, which provide exact values for every position with eight or fewer pieces. How might such databases be efficiently generated, stored and accessed?

  6. 5.6 (if time permits) Discuss how well the standard approach to game playing would apply to games such as tennis, pool and croquet, which take place in a continuous physical state space.