Syntax note

• int argc is the number of arguments given, *argv[] is the array of strings that were given
  • int main(int argc, char **argv) ⇒ you don’t have to write the square bracket this way
• for loop structure: for( initialisation ; terminating condition ; increment )
  • if you forget the following {} brackets after starting the for loop, the loop will only action the first line after it, then it will increment and ction the loop again
  • if you’re using a counter, use a for loop

Switch Statements:

To produce an object file named Graph.o from the source code file Graph.c using the gcc compiler, you can use the following command:

gcc -c Graph.c -o Graph.o

Here's what each part of the command does:

• -c : This option tells the compiler to generate an object file ( .o file) instead of creating an executable. It compiles the source code but does not perform linking.
• Graph.c : This is the input source code file that you want to compile.
• -o Graph.o : This option specifies the name of the output object file that will be generated. In this case, it will be named Graph.o .

So, when you run this command, it will compile the Graph.c source code and create the Graph.o object file containing the compiled code from the source file.

1. Introduction (1 mark):
   • Briefly introduce the context of the question: differentiating between four sorting algorithms without any prior knowledge.
   • Mention the importance of understanding sorting algorithms and their behaviors.
2. Observation of Sorted Data (2 marks):
   • Describe the process of providing each sorting program with already sorted data.
   • Explain the expected behaviors of each algorithm:
     • Bubble Sort: Minimal swaps, primarily adjacent element swaps.
     • Insertion Sort: Few swaps but more shifts to insert elements.
     • Merge Sort: Moderate number of swaps and comparisons due to recursive divisions and merges.
     • Naive Quicksort: Significant swaps and comparisons due to pivot-based partitioning.
3. Observation of Reverse Sorted Data (2 marks):
   • Explain the process of using reverse sorted data as input for each algorithm.
   • Discuss the behaviors observed:
     • Bubble Sort: Maximum swaps required due to multiple passes.
     • Insertion Sort: Fewer swaps than Bubble Sort, but still significant shifts and comparisons.
     • Merge Sort: Similar behavior to sorted data observation.
     • Naive Quicksort: Similar behavior to sorted data observation.
4. Observation of Random Data (2 marks):
   • Describe the step of providing randomly shuffled data to the sorting programs.
   • Discuss the performance trends observed:
     • Bubble Sort: Slowest due to multiple passes through the array.
     • Insertion Sort: Faster than Bubble Sort but slower than more efficient algorithms.
     • Merge Sort: Faster than both Bubble and Insertion Sort due to better time complexity.
     • Naive Quicksort: Faster than Bubble Sort but possibly slower than Merge Sort.
5. Analysis of Code Structure (1 mark):
   • Briefly mention the importance of code analysis in identifying algorithms.
   • Suggest examining specific characteristics unique to each algorithm:
     • Bubble Sort: Focuses on adjacent element comparisons and swaps.
     • Merge Sort: Involves recursive divisions and merges.
     • Insertion Sort: Emphasizes element shifts for insertion.
     • Naive Quicksort: Pivot-based partitioning and recursion.
6. Conclusion (1 mark):
   • Summarize the key observations and analyses made to differentiate the sorting algorithms.
   • Emphasize the importance of these observations in understanding algorithm behaviors.

By organizing your response using these pointers, you can provide a well-structured and comprehensive answer to the 8-mark question about differentiating between the four sorting algorithms.

1. Breadth-First Search (BFS):
   • Time Complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
   • BFS explores a graph level by level, starting from a chosen source vertex.
   • It uses a queue data structure to maintain the order in which vertices are visited.
   • The algorithm begins by enqueueing the source vertex and marking it as visited.
   • For each vertex removed from the queue, BFS visits all of its unvisited neighbors, enqueues them, and marks them as visited.
   • This process continues until the queue becomes empty or the desired condition is met.
   • BFS is commonly used to find the shortest path in an unweighted graph.
2. Depth-First Search (DFS):
   • Time Complexity: O(V + E) , where V is the number of vertices and E is the number of edges in the graph.
   • DFS explores a graph by visiting vertices along a branch as deeply as possible before backtracking.
   • It can be implemented using either recursion or an explicit stack data structure.
   • The algorithm starts from a chosen source vertex and explores its adjacent vertices recursively or iteratively.
   • When visiting a vertex, DFS marks it as visited and continues to explore its unvisited neighbors.
   • DFS keeps backtracking until all possible paths from the current vertex are explored.
   • It is used for tasks such as finding paths, detecting cycles, and traversing trees.
3. Prim's Algorithm:
   • Time Complexity: O(V^2) using adjacency matrix representation or O(E + V log V) using adjacency list representation with a binary heap.
   • Prim's algorithm builds a minimum spanning tree (MST) by greedily adding edges to the tree.
   • It starts with an arbitrary vertex and repeatedly selects the shortest edge that connects a vertex in the MST to a vertex outside the MST.
   • The algorithm maintains two sets: the MST set and the remaining vertices set.
   • It uses a data structure (e.g., priority queue or binary heap) to efficiently select the minimum edge.
   • The process continues until all vertices are included in the MST, forming a tree with minimum total edge weights.
4. Dijkstra's Algorithm:
   • Time Complexity: O((V + E) log V) using a binary heap.
   • Dijkstra's algorithm finds the shortest path from a source vertex to all other vertices in a weighted graph with non-negative edge weights.
   • It maintains a distance value for each vertex, initially set to infinity for all vertices except the source.
   • The algorithm iteratively selects the vertex with the smallest distance and relaxes its adjacent edges, updating the distances if a shorter path is found.
   • Dijkstra's algorithm relies on a priority queue or a min-heap to efficiently select the vertex with the minimum distance.
   • Once the destination vertex is reached or all vertices are processed, the algorithm terminates, and the shortest paths are determined.
5. Kruskal's Algorithm:
   • Time Complexity: O(E log E) or O(E log V), depending on the sorting algorithm used.
   • Kruskal's algorithm constructs a minimum spanning tree (MST) by iteratively adding edges to the tree while avoiding cycles.
   • It starts by sorting all edges in ascending order based on their weights.
   • The algorithm then processes edges one by one, adding an edge to the MST if it doesn't create a cycle with the previously added edges.
   • To check for cycles, a disjoint-set data structure (often implemented using a union-find algorithm) is used.
   • Kruskal's algorithm continues until the MST includes all vertices or until a certain condition is met, resulting in a tree with minimum total edge weights.

Each of these algorithms has its own specific application and advantages, and they are commonly used for various graph-related problems in computer science and other fields.

Linked List
///////////////////////////////////////////////////////////////////
//Intializing a Node
struct node 
{
    int data;
    struct node *next;
}
///////////////////////////////////////////////////////////////////
//Code of adding a new node to the head
struct node *current = head;
struct node *new_node = malloc(sizeof(struct node));
new_node->data = data;
new_node->next = NULL;
if (head == NULL)
{
    head = head->next;
    current->next = NULL;
    free(current);
}
///////////////////////////////////////////////////////////////////
// Add at the end of the list
struct node *current = head;
struct node *new_node = malloc(sizeof(struct node));
new_node->data = data;
new_node->next = NULL;
while (current->next != NULL)
{
    current = current->next;
}
current->next = new_node;
new_node = NULL;
///////////////////////////////////////////////////////////////////
// Code of adding at the nth position
struct node *insert_nth(int n, int value, struct node *head){
    struct node *current = head;
    struct node *previous = NULL;
    struct node *new_node = malloc(sizeof(struct node));
    new_node->data = data;
    new_node->next = NULL;
    int length = 0;
    while (current != NULL)
    {
        current = current->next;
        length++
    }
    current = head;
    if (n == 0 && head == NULL)
    {
        head = new_node;
        new_node = NULL;
    }
    else if (n== 0 && head != NULL)
    {
        new_node->next = current;
        head = new_node;
    }
    else if (n > 0 && n < length)
    {
        int count = 0;
        while (current != NULL && count < n)
        {
            previous = current;
            current = current->next;
            count++;
        }
        new_node->next = current;
        previous->next = new_node;
    }
    else if (n >= length)
    {
        int count = 0;
        while (current->next != NULL && count < n)
        {
            current = current->next;
        }
        current->next = new_node;
        new_node->next = NULL;
    }
}
///////////////////////////////////////////////////////////////////
// Deleting at 'said' data from the list 
struct node *current = head;
struct node *previous = NULL;
if (head->data = data)
{
    head = head->next;
    free(current);
}
else if (head->data != data)
{
    while (current != NULL && head->data != data)
    {
        previous = current;
        current = current->next;
    }
    previous->next = current->next;
    current->next = NULL
    free(current);
}
///////////////////////////////////////////////////////////////////
/// Linked List implementation of Stack
// Stack is LIFO structure
// Inserts at the top
void Push(int data)
{
    // Here top is head. //This is insertion at the beginning of the list
    struct node *top = NULL; // my stacks empty
    struct node *new_node = malloc(sizeof(struct node));
    new_node->data = data;
    new_node->next = top;
    top = new_node;
}
// Deletes from the top (can be made to duplicate from the top)
void Pop()
{
    if (top == NULL)
    {
        return;
    }
    struct node *temp = top;
    top = top->next;
    free(temp);
}
////////////////////////////////////////
/// The Parenthesis Problem \\\\\\\
/* Conditions for a the Problem
    1. While popping the stack must not be underflowing
    2. At end of the expression (loop), the stack must be Empty. 
    3. If '(' then we push into the stack, If ')' then we remove from the stack.
*/ 
////////////////////////////////////////
// Single Parenthesis Method
while (scanf("%c", &user_input) == 1)
{
    parenthesisMatch(user_input);
}
int parenthesisMatch(char user_input){
    // Create and initialize the stack
    if(user_input =='(')
    {
        push(sp, '(');
    }
    else if(char user_input ==')')
    {
        if(isEmpty(sp))
        {
            return 0;
        }
        pop(sp); 
    }
    if(isEmpty(sp))
    {
        return 1;
    }
    else
    {
        return 0;
    } 
}
////////////////////////////////////////
// Multiple Parenthesis Method 
while (scanf("%c", &user_input) == 1)
{
    parenthesisMatch(user_input);
}
int match (char popped_char, char user_input)
{
    if (user_input == '(' && popped_char == ')')
    {
        return 1;
    }
    else if (user_input == '[' && popped_char == ']')
    {
        return 1;
    }
    else if (user_input == '{' && popped_char == '}')
    {
        return 1;
    }
}
int parenthesisMatch(char user_input){
    // Create and initialize the stack in the main.
    if(user_input =='('|| user_input == '{' || user_input == '[')
    {
        push(sp, user_input);
    }
    else if (user_input ==')'|| user_input == '}' || user_input == ']' )
    {
        if(isEmpty(sp))
        {
            return 0;
        }
        char popped_char == pop(sp); 
        if (match (popped_char, user_input) == 1) // If the stack's topmost element doesn't match then, with the user input,
        {                              // Then we stop further checking.
            return 0; 
        }
    }
    if(isEmpty(sp))
    {
        return 1;
    }
    else
    {
        return 0;
    } 
}
///////////////////////////////////////////////////////////////////
// Reversing the Linked List 
struct node *current = head;
struct node *previous = NULL;
struct node *next = head->next;
while (current != NULL)
{
    current->next = previous;
    previous = current;
    current = next; 
    next = next->next;
}
head = previous;
///////////////////////////////////////////////////////////////////
/// Implementation of the Circular Linked List 
// To traverse the list, we need to state Current != head;
struct node *current = head;
current = current->next;
while (current != head)
{
    current = current->next;
}
// Add at the end of the circular linked list 
struct node *new_node = malloc(sizeof(struct node));
new_node->data = data;
new_node->next = NULL;
struct node *current = head->next;
while (current->next != head) // Will make it stop at the last node
{
    current = current->next;
}
new_node = head;
current->next = new_node;
///////////////////////////////////////////////////////////////////
// Shifting the Linked List by K to the Right
// If moving to the right by K --> Traverse_list = Length - K
// If moving to the left by K --> Traverse_list = K
struct node *current = head;
struct node *second_list = NULL;
int length = 1;
while (current != NULL)
{
    current = current->next;
    length++;
}
current = head;
int itterate_by = length - user_move_by;
int count = 1;
while (current != NULL && count < itterate_by)
{
    current = current->next;
    count++;
}
second_list = current->next;
current->next = NULL;
struct node *new_current = second_list;
while (new_current->next != NULL)
{
    new_current = new_current->next;
}
new_current->next = head;
head = second_list;
///////////////////////////////////////////////////////////////////
// Linked List Implementation of a Queue
// We need to store the head and tail in this situation for dequeue and enqueue in the list
struct node *head = NULL;
struct node *rear = NULL; 
void enqueue(int data)
{
    struct node *new_node = malloc(sizeof(struct node));
    new_node->data = data;
    new_node->next = NULL;
    if (head == NULL && rear == NULL)
    {
        head = new_node;
        rear = new_node;
    }
    else if (head != NULL & rear != NULL)
    {
        rear->next = new_node;
        rear = new_node; 
    }
}
void dequeue()
{
    struct node *current = head;
    if (head == NULL)
    {
        return;
    }
    else if (head == rear)
    {
        head = NULL;
        rear = NULL;
    }
    else 
    {
        head = head->next;
    }
    free(current);
}

find length of string using strlen(string)

NOTE: requires string.h library

.

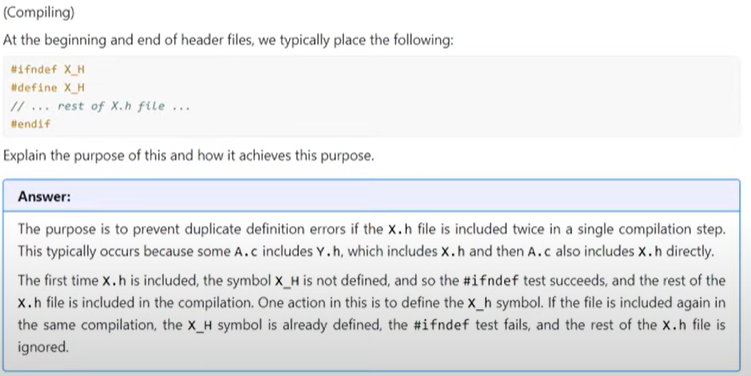
Malloc requires the stdlib.h header file to function.

Note: malloc does not intialise the memory it allocates. If you want to initialise the memory to a specific value, you can use calloc, which works similar to malloc but sets all bytes of the allocated memory to zero.Here are a few examples on malloc memory allocation:

// Allocate memory for an int
int* ptr = (int*)malloc(sizeof(int));
int* ptr = malloc(sizeof(int)); 
// Allocate memory for a char
char* ptr = (char*)malloc(sizeof(char));
char* ptr = malloc(sizeof(char));
// Allocate memory for a string with a maximum of 100 characters (including the null terminator) 
char* ptr = (char*)malloc(100 * sizeof(char));
char* ptr = malloc(100 * sizeof(char));
// Allocate memory for a struct
struct node {
      int value; 
      struct node *next; 
}; 
struct node* newNode = (struct node*)malloc(sizeof(struct node));
struct node* newNode = malloc(sizeof(struct node));
// Allocate memory for an array of 5 integers 
int* ptr = (int*)malloc(5 * sizeof(int));
int* ptr = malloc(5 * sizeof(int));

When using malloc, make sure to check whether the memory allocation is successful.

ptr = (int*)malloc(size * sizeof(int));
if (ptr == NULL) { 
    // Print an error message to the standard error stream (stderr)
    fprintf(stderr, "Memory allocation failed. Exiting the program.\n"); 
     // Exit the program with an error code
    exit(1);
}

Lastly, don't forget to free the memory using 'free' when you are done using the variable(s) to avoid memory leaks.

free(ptr);

struct cell x = { 1 , 2 }; // cell (1, 2)

struct cell a = {. row = 1 , . col = 2 }; // also cell (1, 2) but more explicit

struct cell y = { x . row , x . col + 1 }; // this is the cell to the right of x

struct cell z = x ; // this is a copy of x z . row = z . row + 1 ; // this modifies z to be the cell under it

type variable_name = value;

sim needs to remember to put types when making new variables. python brained.

'''
printf("Hello, world!\n")

'''