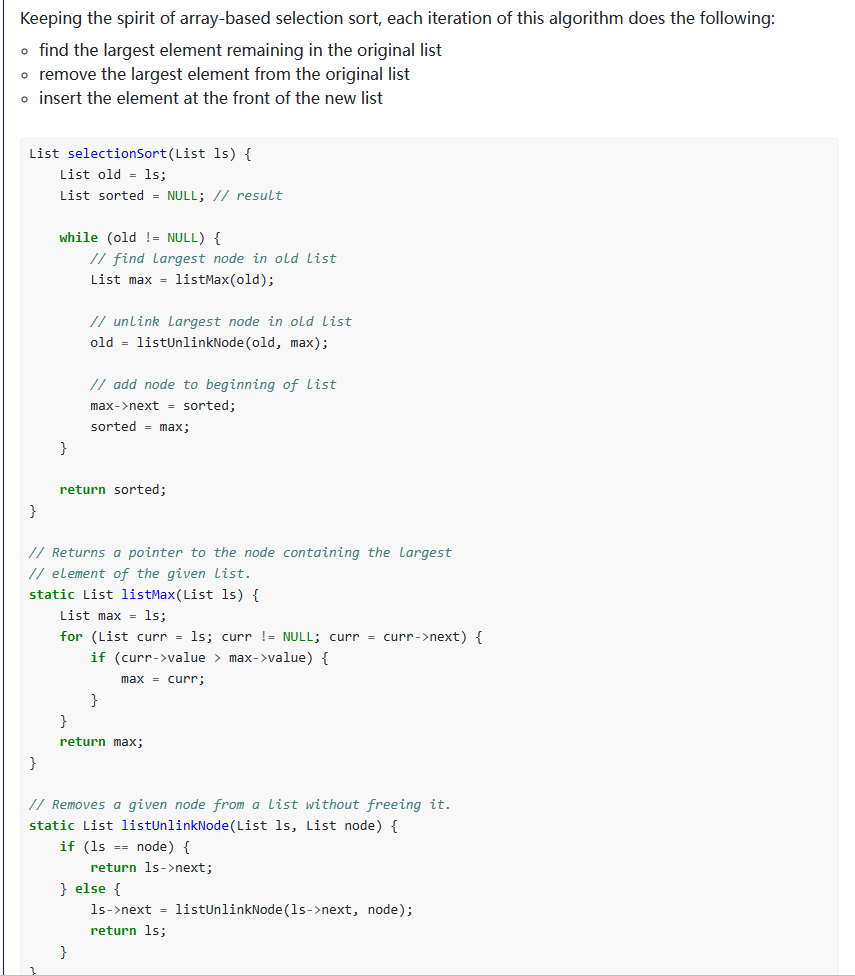
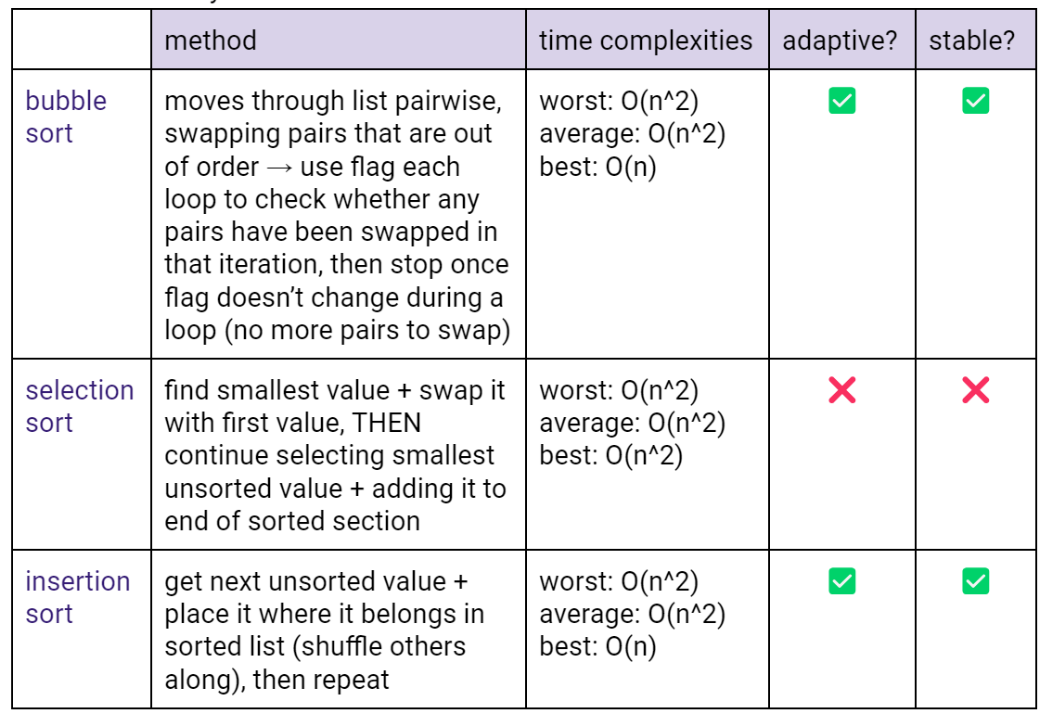
Sorting Overview:
Basic Sorts:
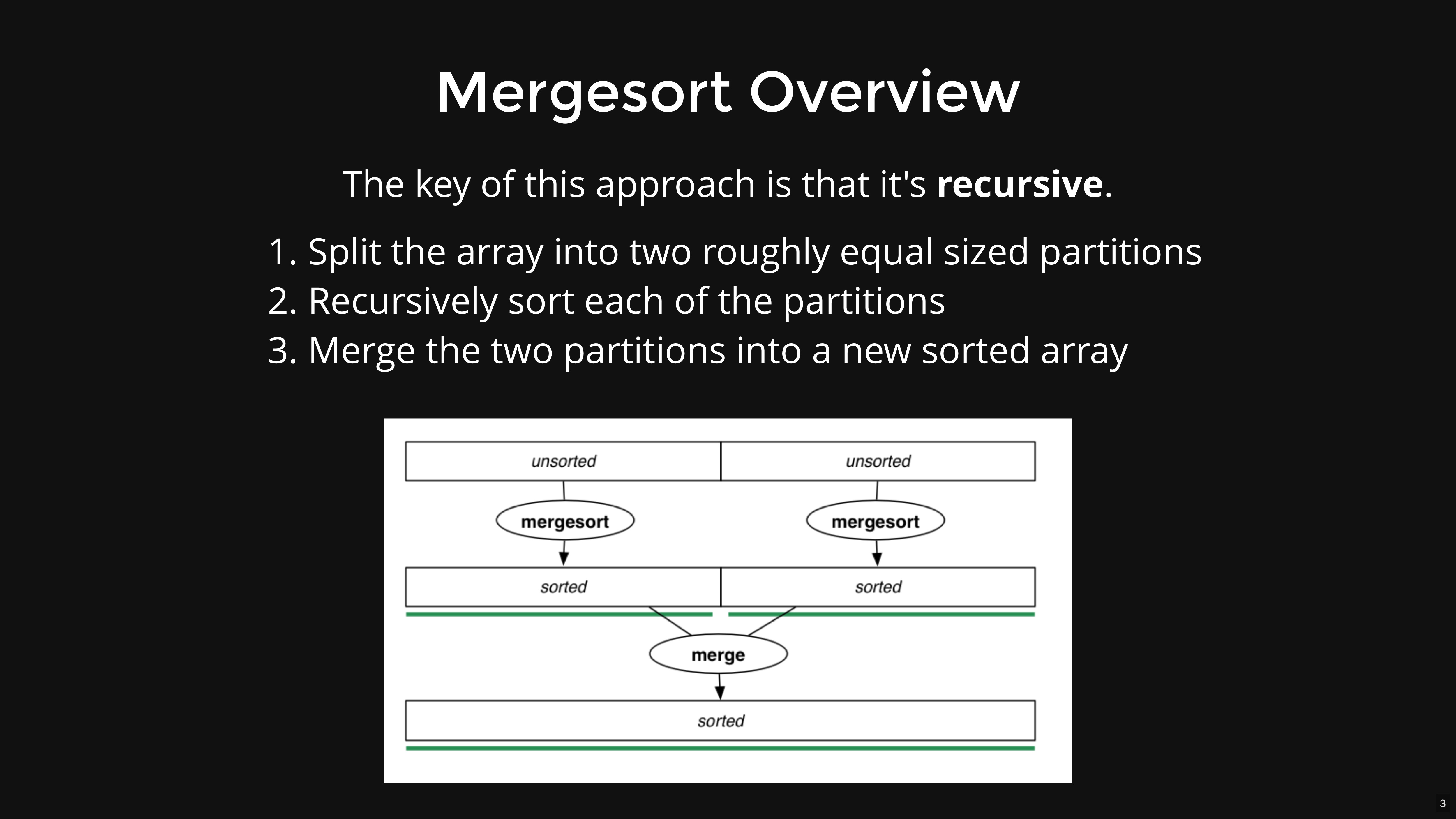
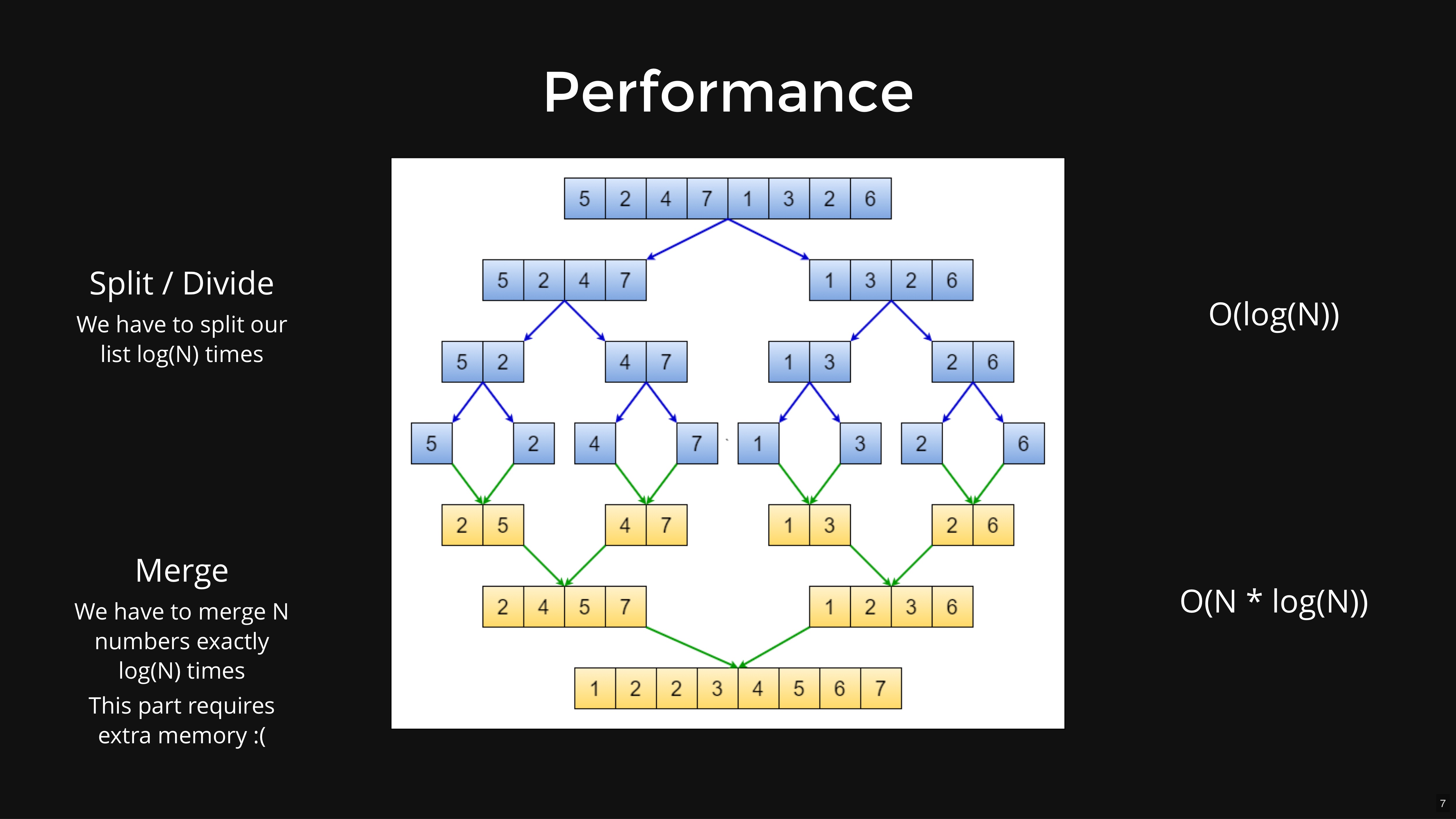
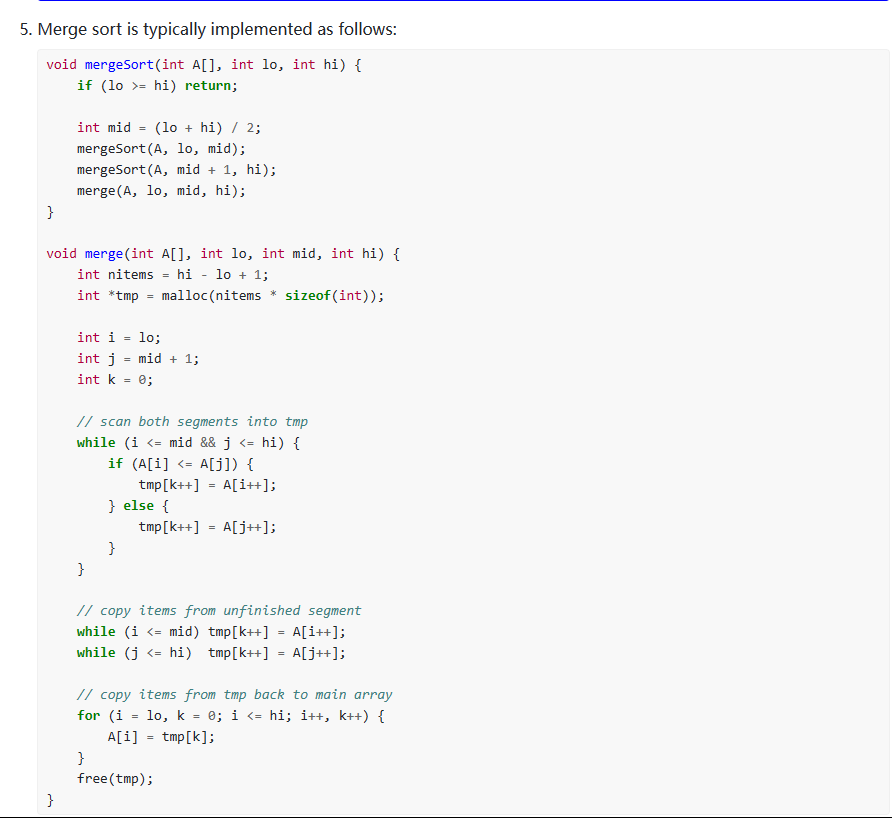
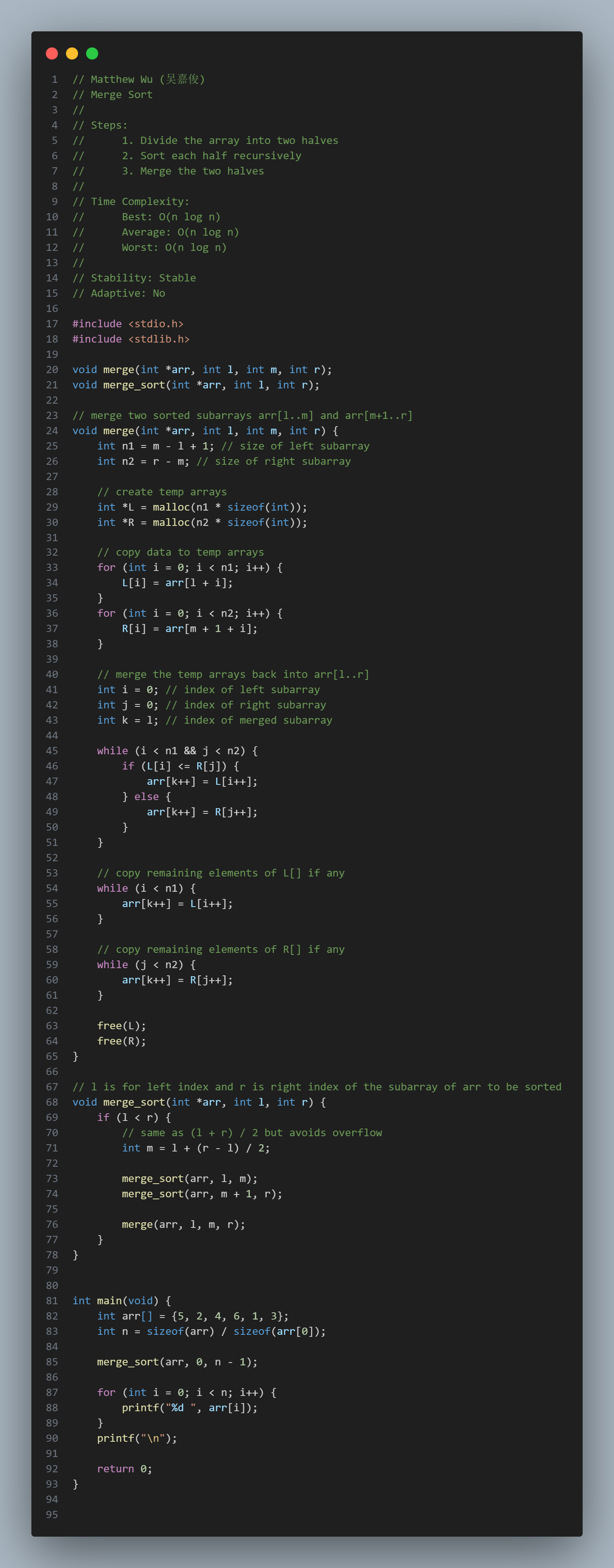
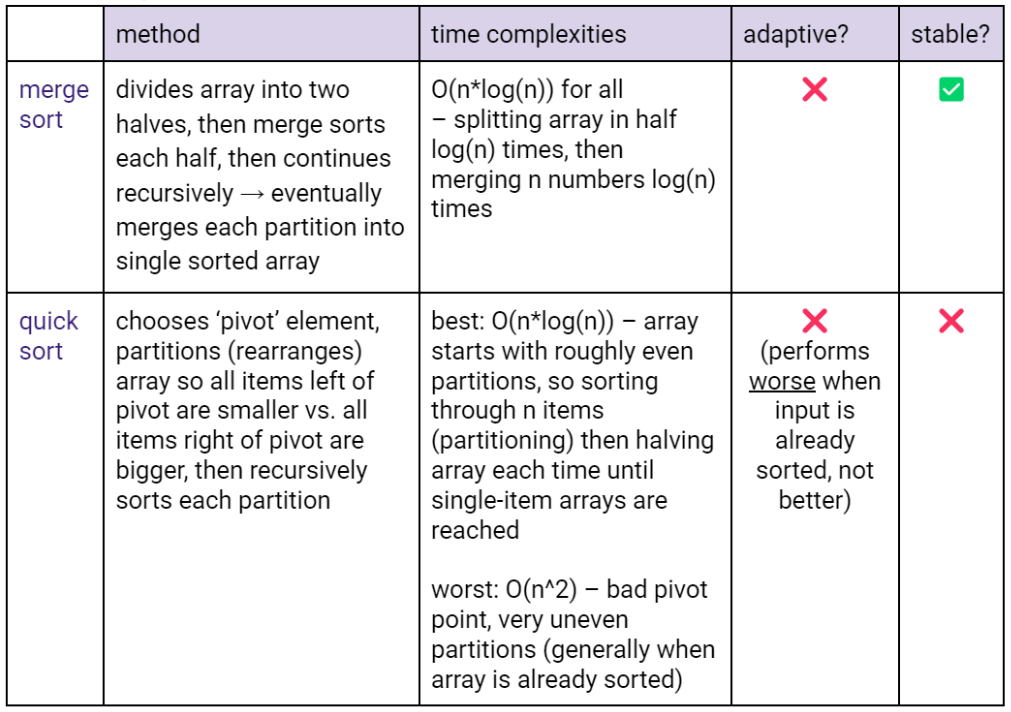
Merge Sort:
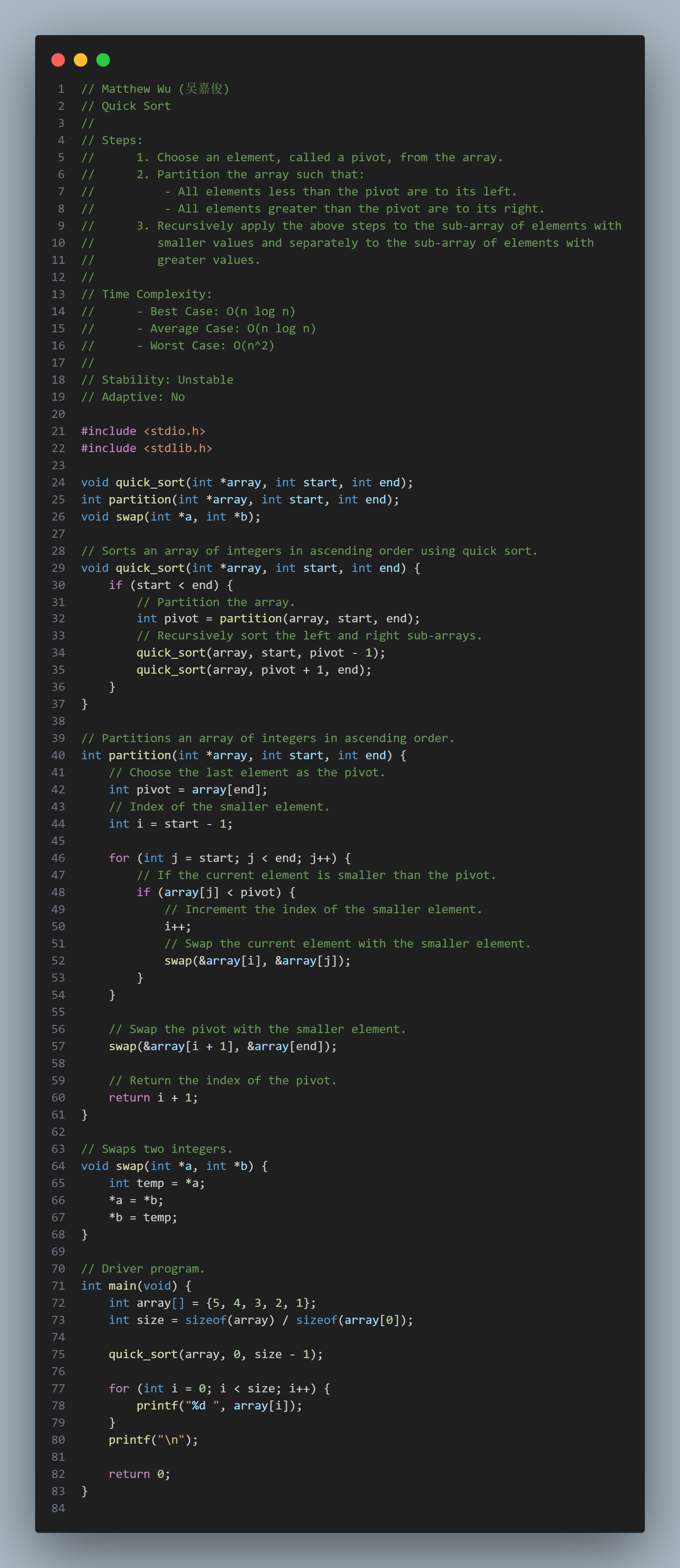
Quick Sort:
Stable or Unstable?
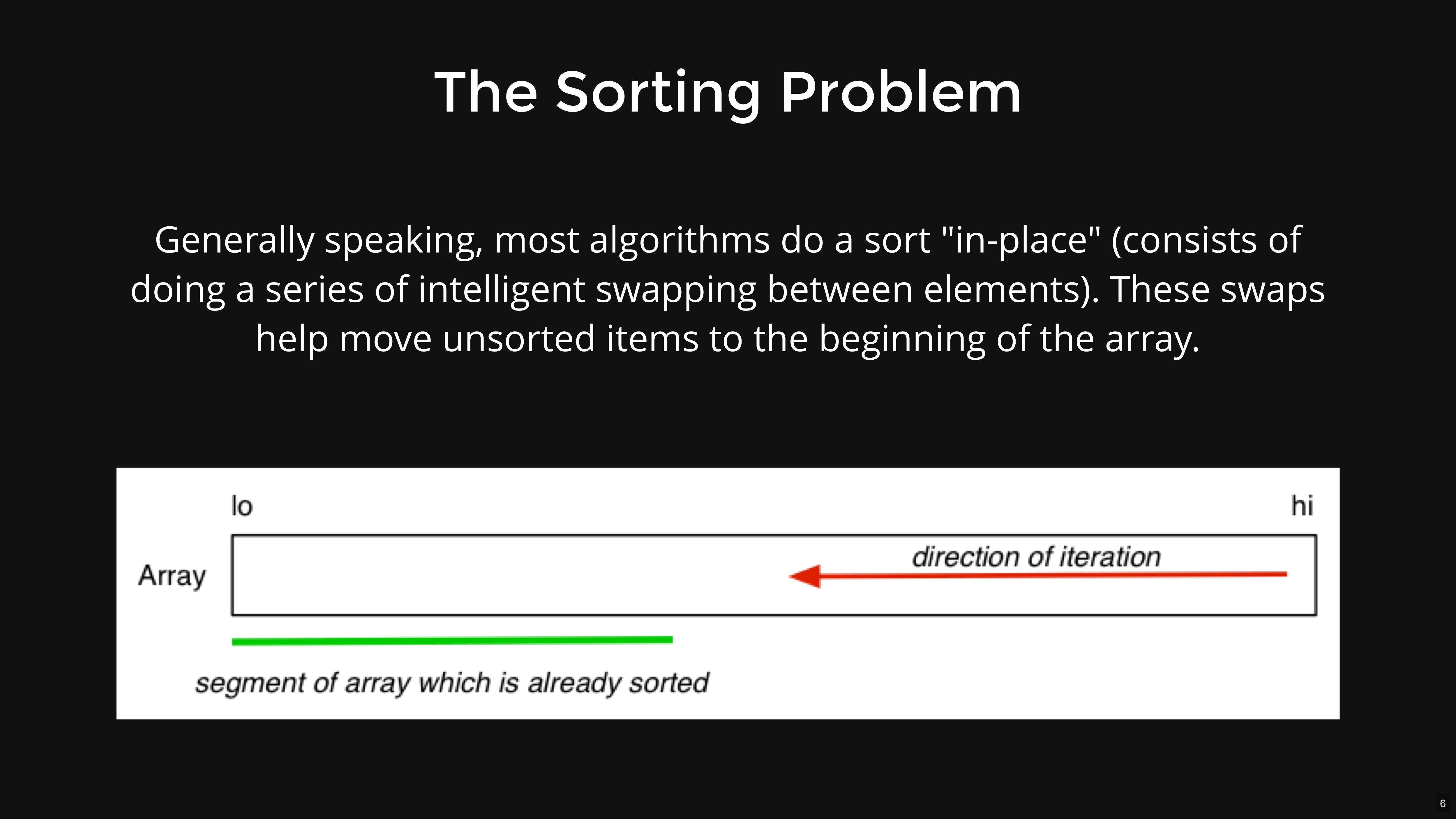
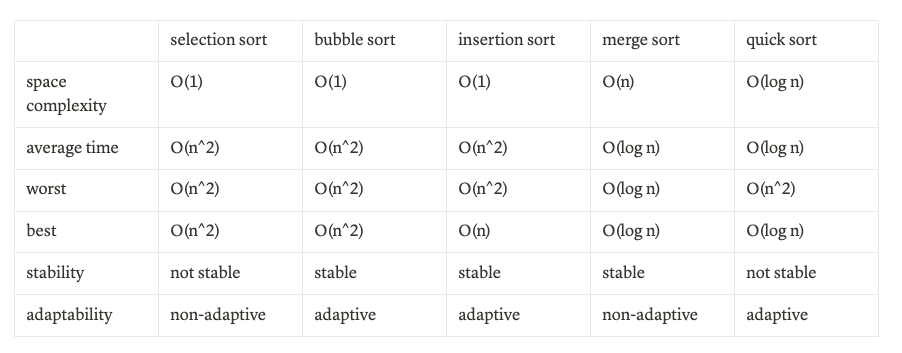
Properties of Sorting Algorithms
Sorting Overview:
Basic Sorts:
Merge Sort:
Quick Sort:

annotated lecture slides







Annotated lecture slides






Annotated lecture slides















Annotated lecture slides








1


sorting algorithms
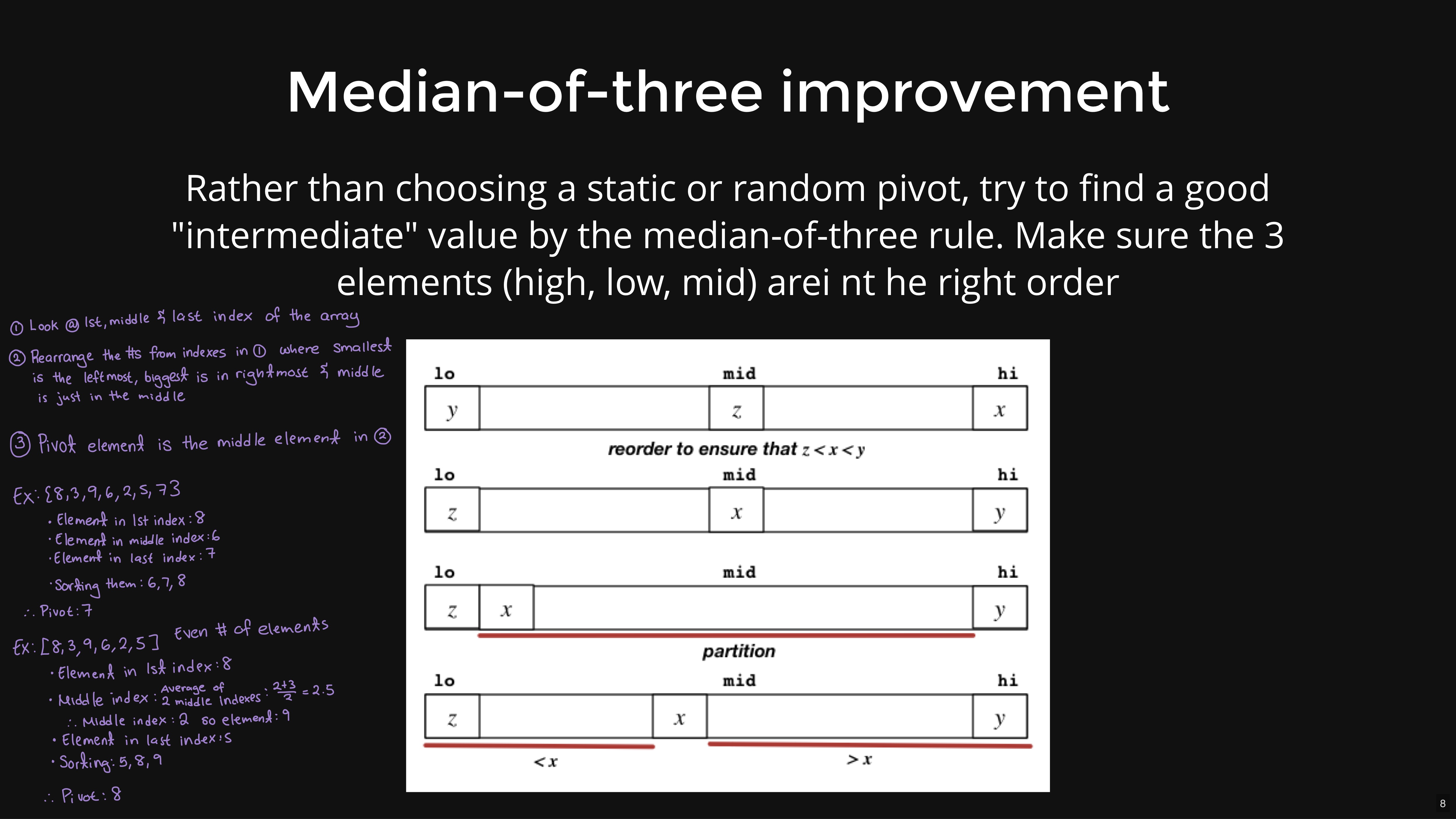
Quick sort
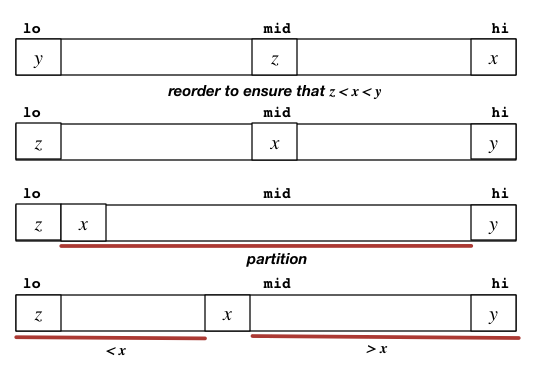
- MOT (Median of three): first index, last index, middle index and find median as a pivot
- random: random pivot
- naive: pick a pivot with fixed strategy
(average O(n log n), worst O(n^2))
Quick Sort pseudocode
int array a initialise
if start >= end, return
int key = start, i = start + 1, j = end, temp
start while loop i <= j
while i <= end && a[i] <=a[key] -> i++;
while j <= start && a[j] >=a[key] -> j--;
if i > j -> swap(a[key], a[j])
else swap(a[i], a[j])
end while loop
call recursion(start, j - 1)
call recursion(j + 1, end)
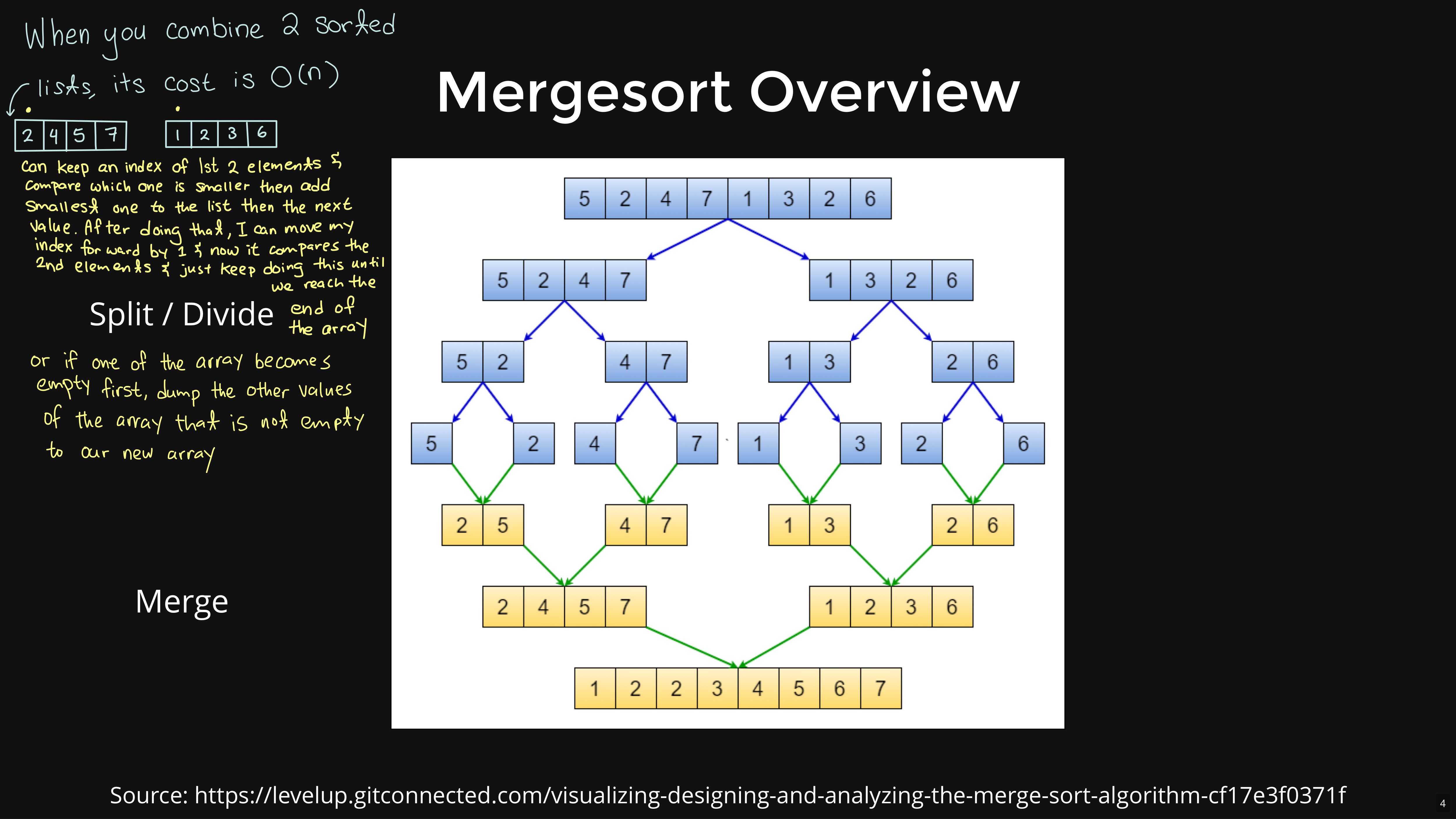
Merge sort pseudocode
<main>mergeSort call with list, start index and arraySize - 1(end index)
<merge sort>
int mid
if left < right (start and end index)
mid = (left + right) / 2 // list divide
recursive call(list, left, mid) // list 1 conquer
recursive call (list, mid + 1, right) // list 2 conquer
call merge (list, left, mid, right) // combining list 1 and list 2
<merge>
int i = left, j = mid +1, k = left,
int L
make int array sorted
start while loop i <= mid AND j <= right // combine two list
if list [i] <= list[j] => sorted[k++] = list[i++]
else sorted[k++] = list[j++]
end while loop
// pick leftovers
if i > mid
for L = j, L <= right -> sorted[k++] = list[L]
else
for L = i, L <= mid -> sorted[k++] = list[L]
// copy sorted(temporary) array to list
for L=left, L <= right -> list[L] = sorted[L]
insertion sort pseudocode (e.g. struct road sort)
- starts with index 1 since we can consider index 0 is already sorted
start for loop i = 1 & i < array size
struct road r = array[i] // copy inserting value
int j is same with i
start while loop when j is greater than 0 AND r's value is smaller than array[j-1]'s value
array[j] = array[j-1]
decrease index j
end while loop
array[j] is set by r
end for loop
int temp
start for loop i < array length
start for loop j < array length - 1 - i
if array [j] > array [j+1]
swap array[j] and array[j +1] using temp
end if
end for j loop
end for i loop
in first for loop, the biggest number will move at the end (reason why arraylength -1 - i)
selection sort pseudocode
int temp;
start for loop i < array length - 1 // no need to compare the final one
start for loop j = i + 1, j < array length
if data of i > data of j
swap i and j using temp
end if
end for j loop
end for i loop
it is possible for an unstable sorting algorithm to produce the same output as a stable sorting algorithm.
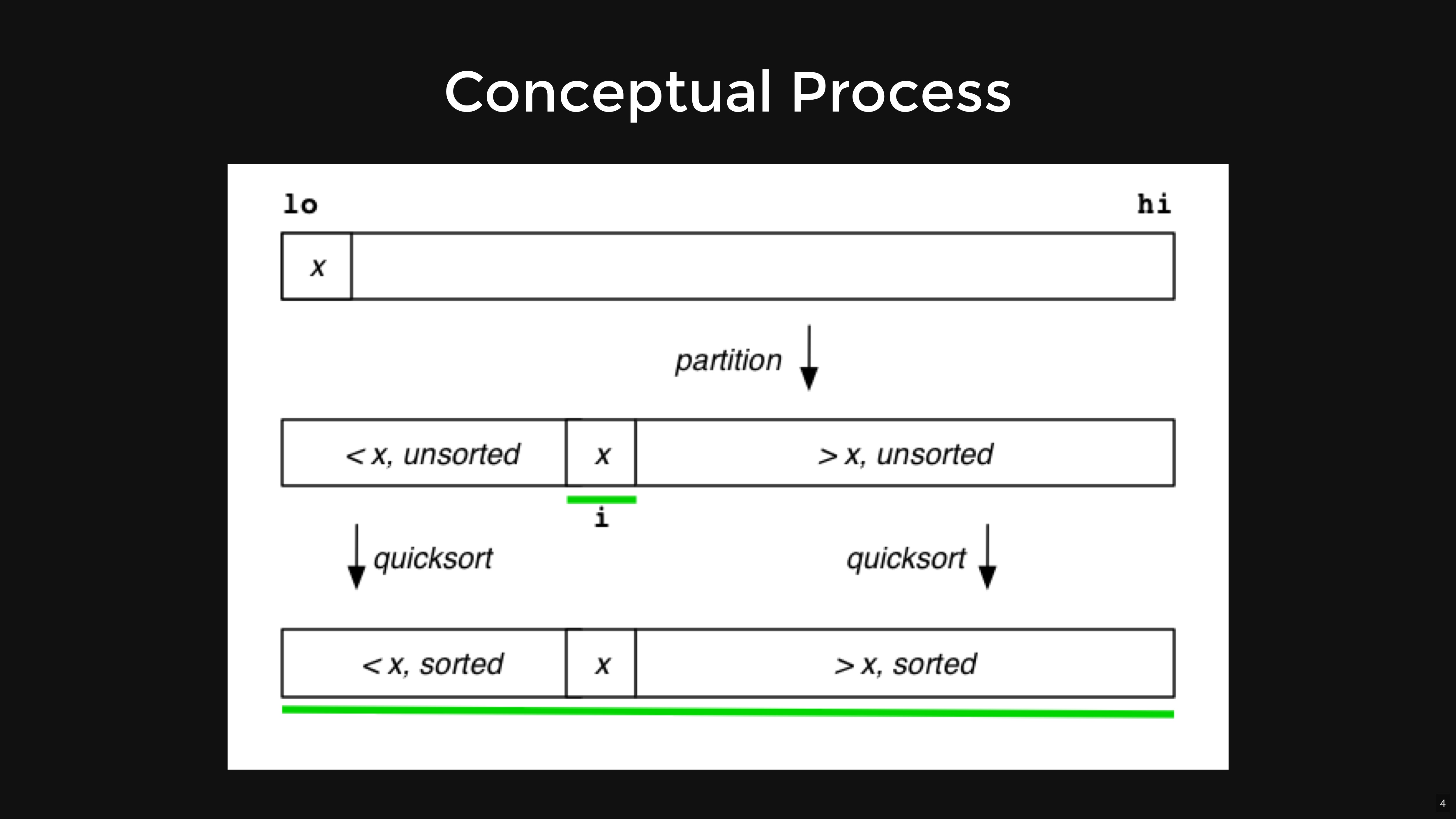
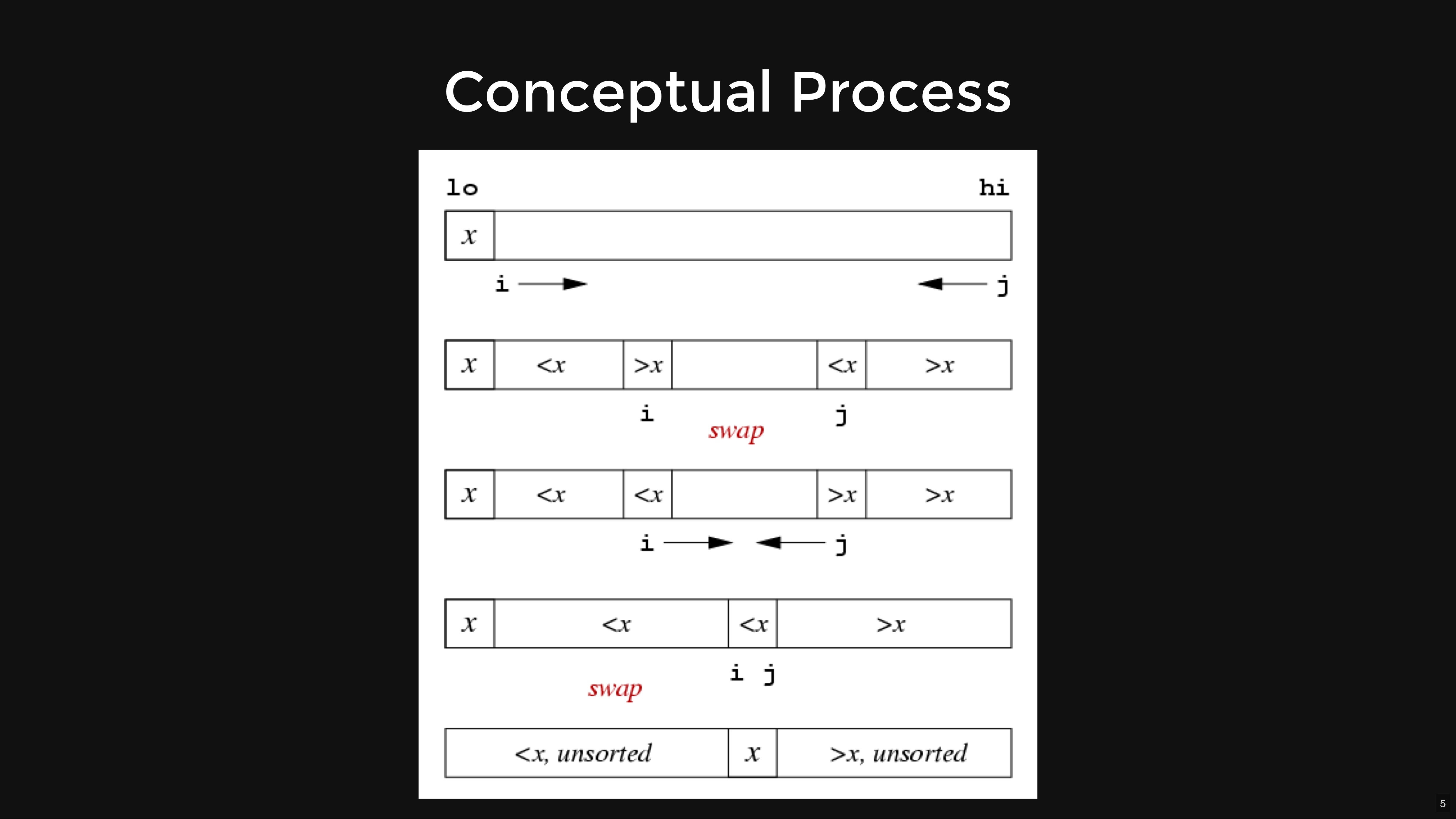
Quick Sort
Steps:Stability: Unstable
Adaptive: No
Merge Sort
Steps:
Time Complexity:
Stability: Stable
Adaptive: No
void quicksort(Item a[], int lo, int hi) { int i; // index of pivot if (hi <= lo) return; medianOfThree(a, lo, hi); i = partition(a, lo+1, hi-1); quicksort(a, lo, i-1); quicksort(a, i+1, hi); } void medianOfThree(Item a[], int lo, int hi) { int mid = (lo+hi)/2; if (less(a[mid],a[lo])) swap(a, lo, mid); if (less(a[hi],a[mid])) swap(a, mid, hi); if (less(a[mid],a[lo])) swap(a, lo, mid); // now, we have a[lo] ≤ a[mid] ≤ a[hi]// swap a[mid] to a[lo+1] to use as pivot swap(a, lo+1, mid); } int partition(Item a[], int lo, int hi) { Item v = a[lo]; // pivot
int i = lo+1, j = hi; for (;;) { while (less(a[i],v) && i < j) i++; while (less(v,a[j]) && j > i) j--; if (i == j) break; swap(a,i,j); } j = less(a[i],v) ? i : i-1; swap(a,lo,j); return j; }
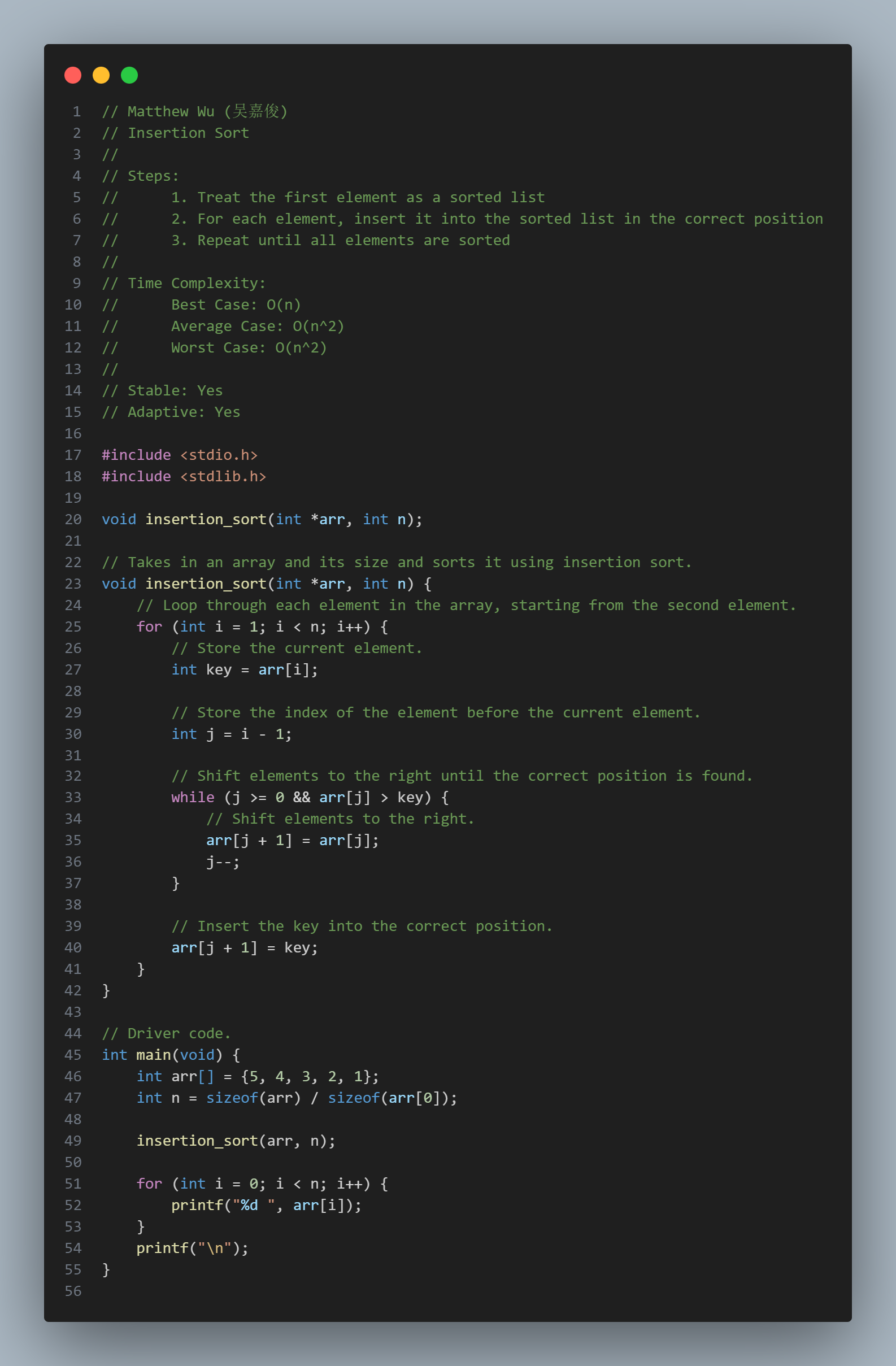
Insertion Sort
Steps:
Stable: Yes
Adaptive: Yes
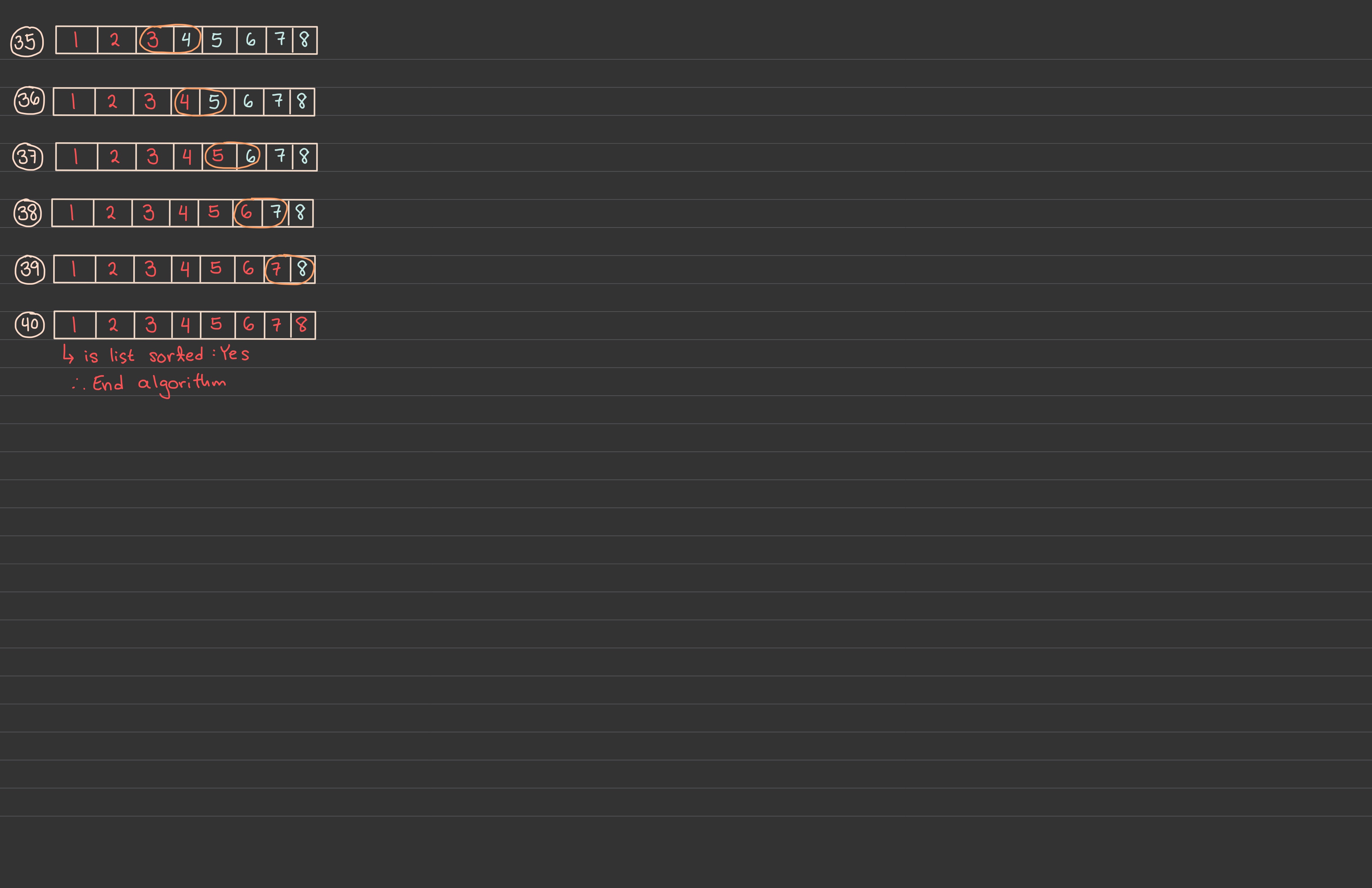
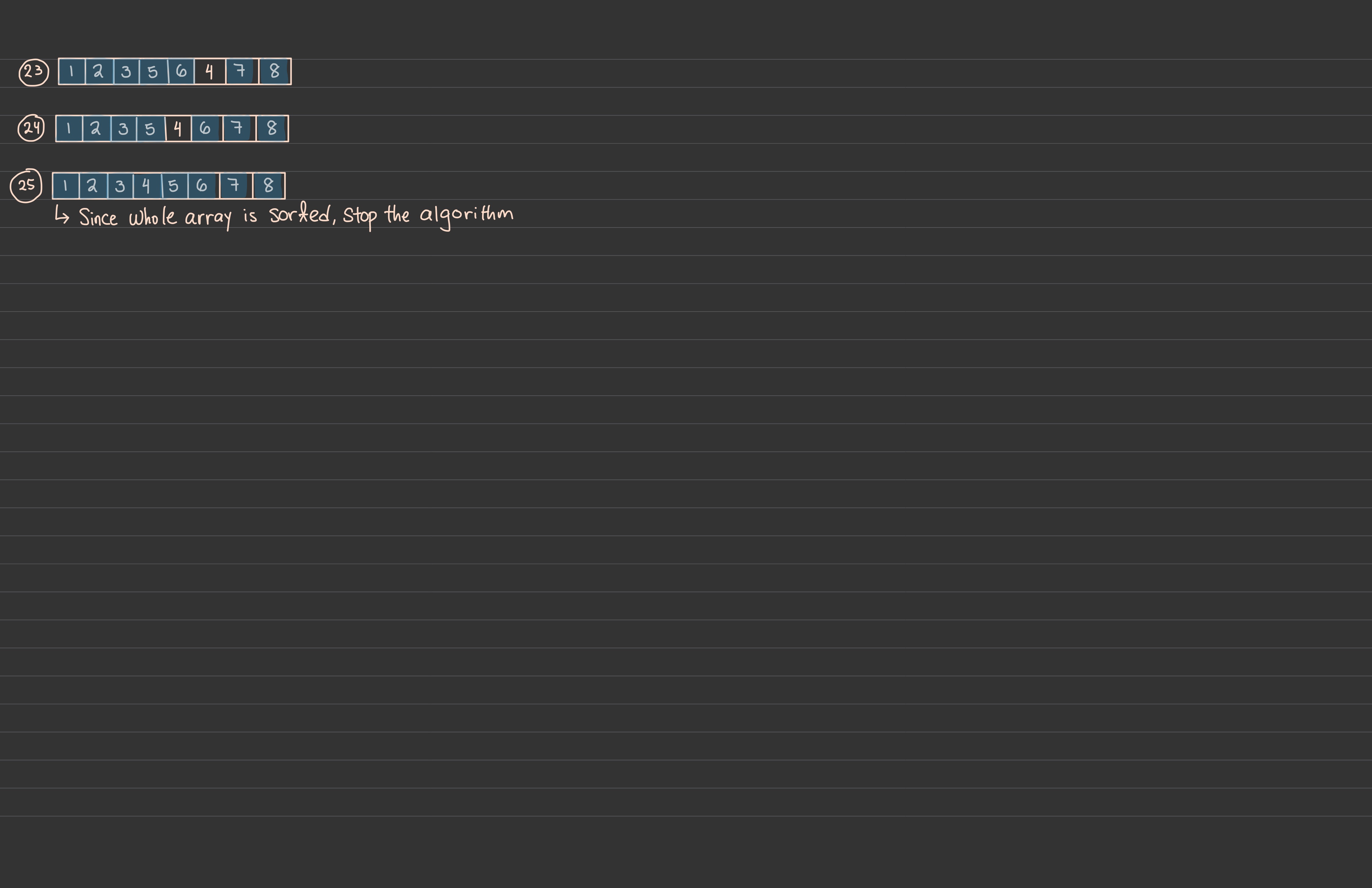
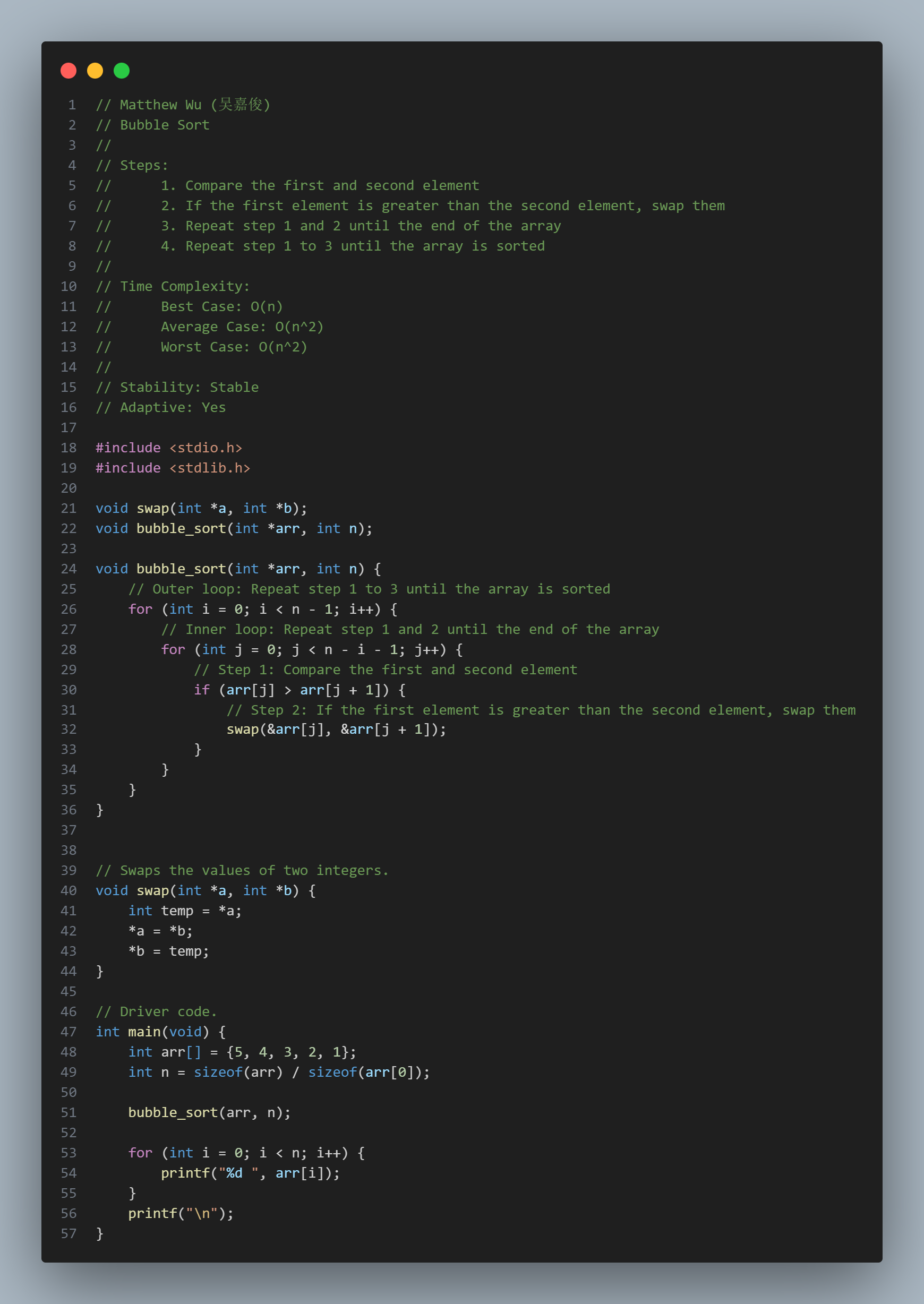
Bubble Sort
Steps:
Time Complexity:
Stability: Stable
Adaptive: Yes
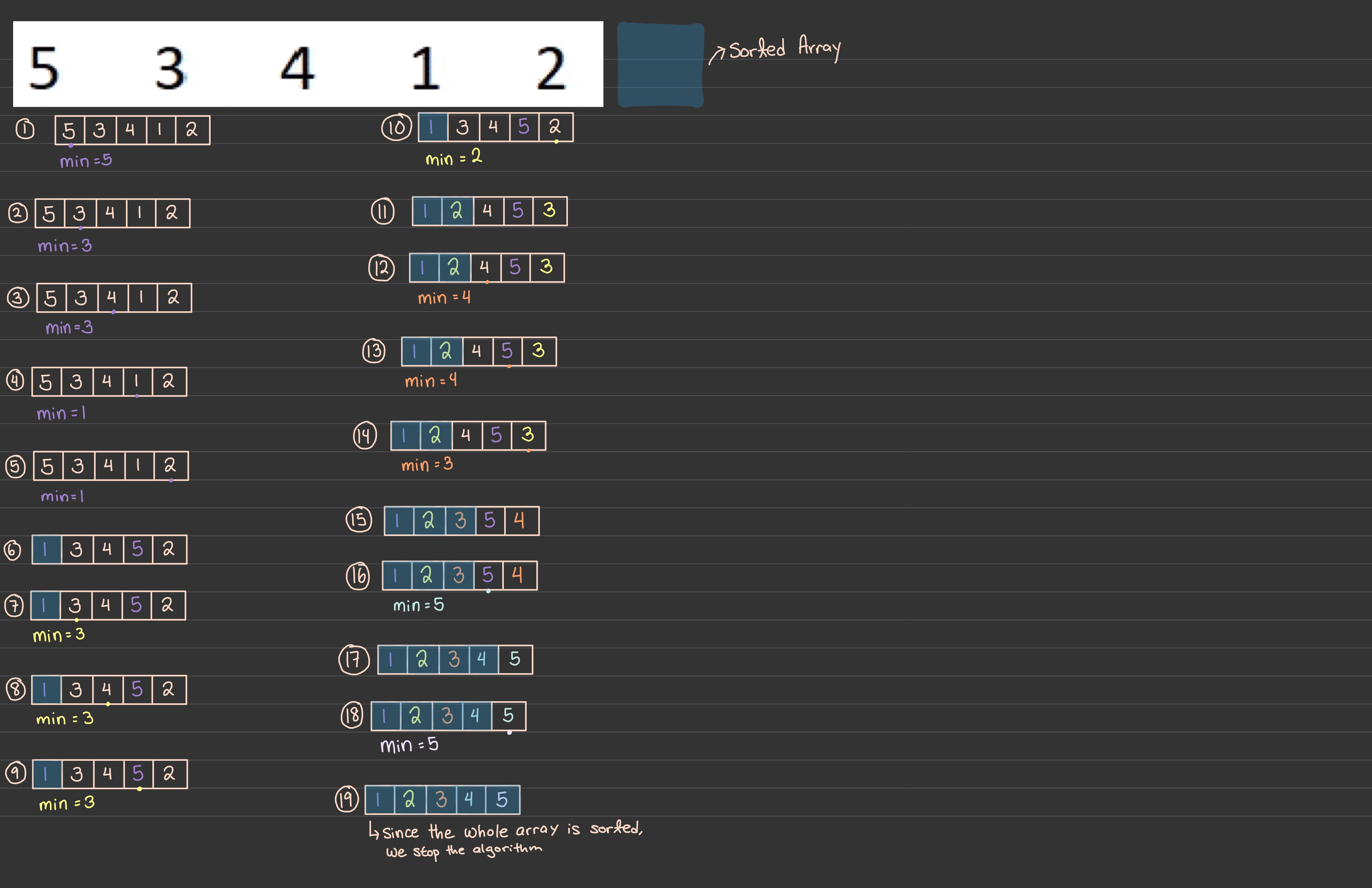
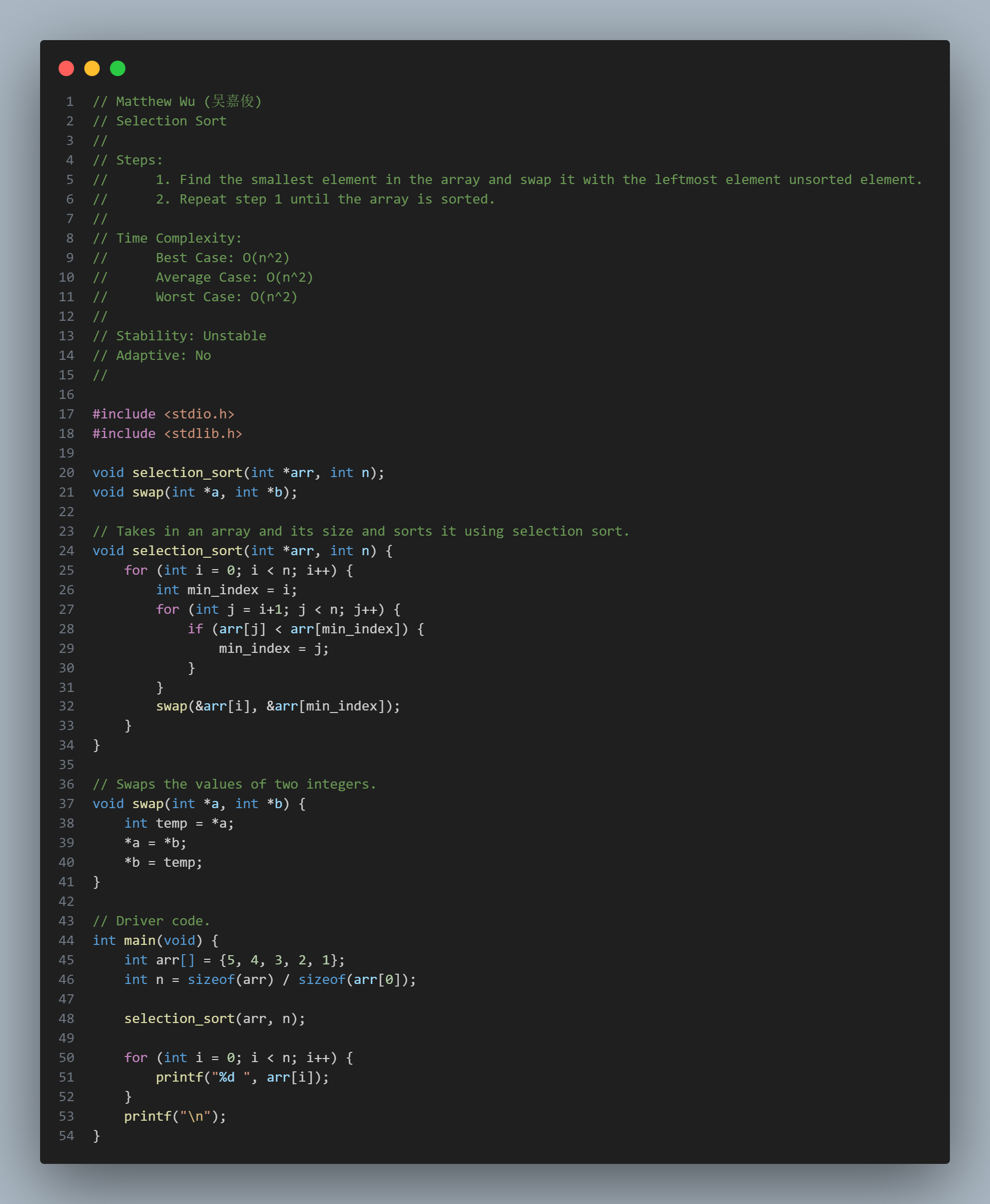
Selection Sort
Steps:
Time Complexity:
Stability: Unstable
Adaptive: No
performs selection sort on a linkedlist
List selectionSort(List ls) {
List old = ls;
List sorted = NULL; // result
while (old != NULL) {
// find largest node in old list
List max = listMax(old);
// unlink largest node in old list
old = listUnlinkNode(old, max);
// add node to beginning of list
max->next = sorted;
sorted = max;
}
return sorted;
}
// Returns a pointer to the node containing the largest
// element of the given list.
static List listMax(List ls) {
List max = ls;
for (List curr = ls; curr != NULL; curr = curr->next) {
if (curr->value > max->value) {
max = curr;
}
}
return max;
}
// Removes a given node from a list without freeing it.
static List listUnlinkNode(List ls, List node) {
if (ls == node) {
return ls->next;
} else {
ls->next = listUnlinkNode(ls->next, node);
return ls;
}
}
selection sort gif

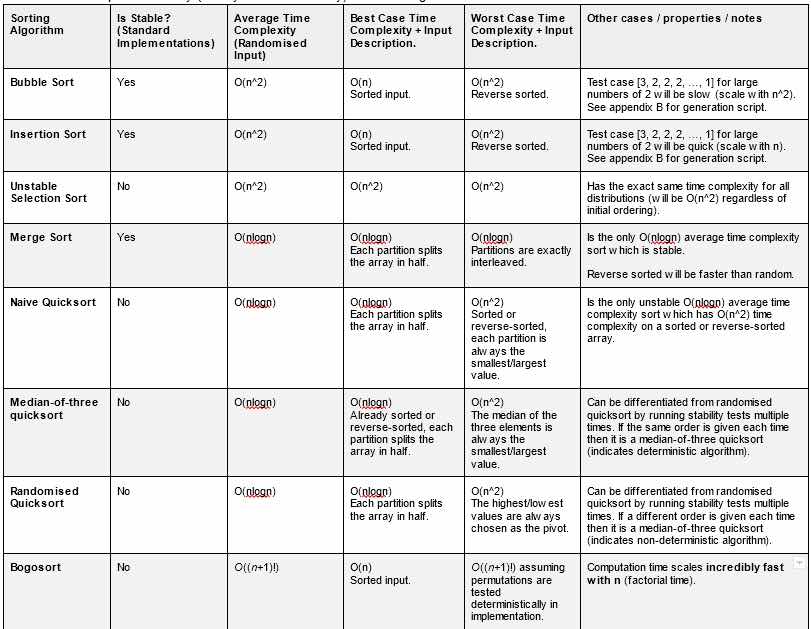
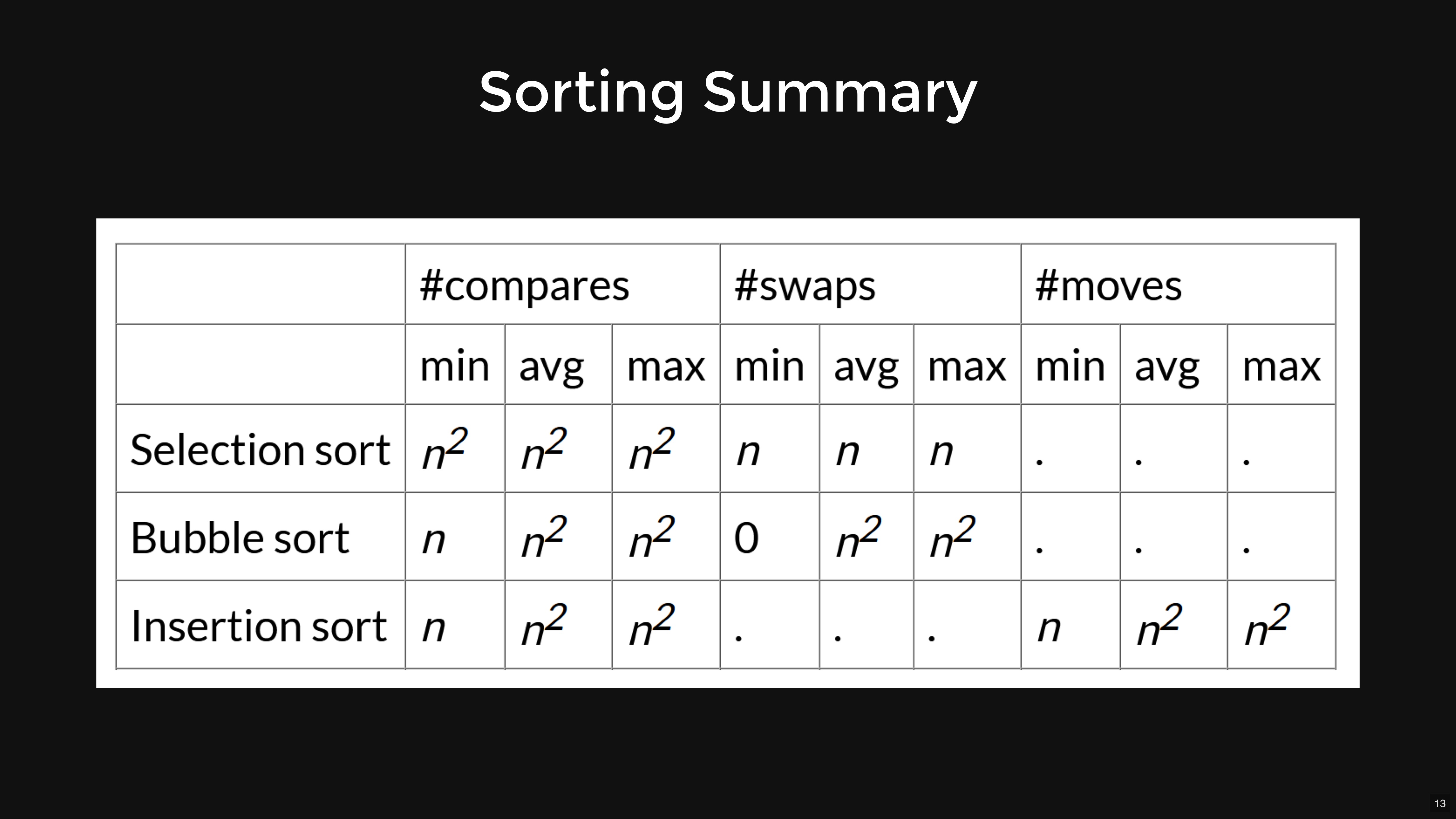
Table of All Sorting Algorithms:
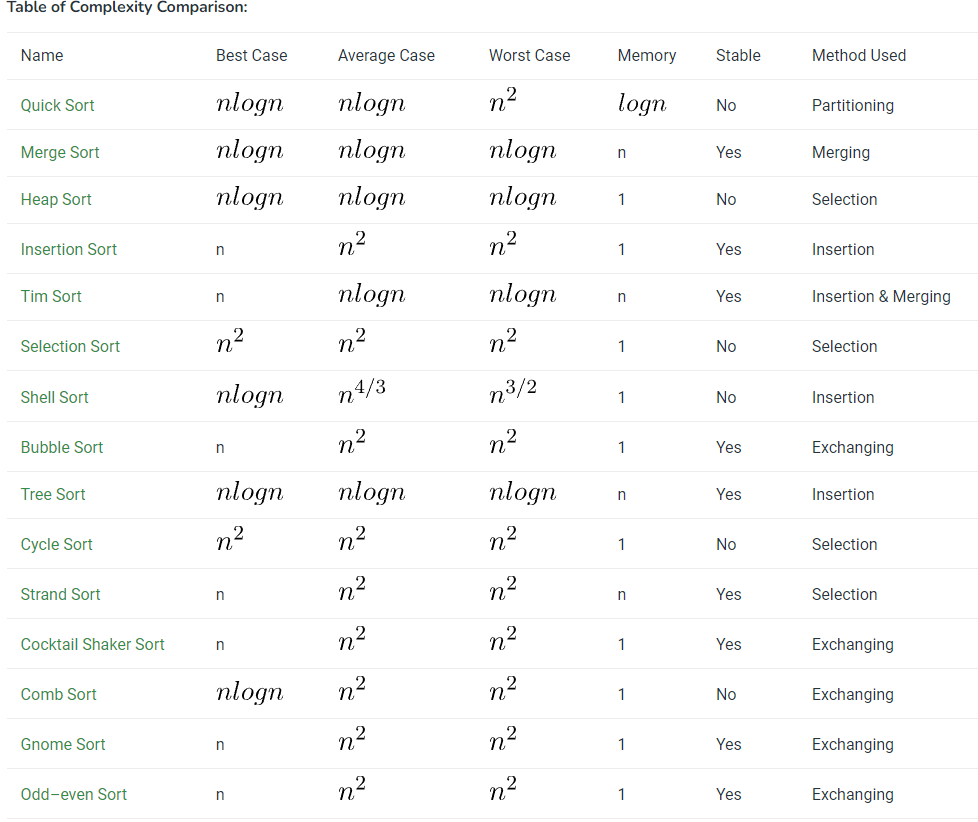
Properties of Sorting Algorithms
#include <stdio.h>
#include <stdlib.h>
#include "Sort.h"
// Helper function to swap elements `array[i]` and `array[j]` in an array
void swap(int *array, int i, int j)
{
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
/**
* Sorts the array of ints
*
* Input:
* - int *array: An array of ints
* - int size: Number of elements in the array
* Output:
* - void
*/
void sort(int *array, int size) {
//3 cursors - low, curr, high
//low: First index of unsorted partition
//High: Last index of unsorted partition
//curr: index of current unsorted element
int low = 0;
int curr = 0;
int high = size - 1;
//Sort until curr cursor passes high cursor, as anything to right of
//high cursor is guarenteed to be sorted from previous sorts
while (curr <= high) {
//Case1: current element is 0
if (array[curr] == 0)
{
swap(array, low, curr);
low++;
curr++;
}
//Case2: current element is 2
else if (array[curr] == 2)
{
swap(array, curr, high);
high--;
}
//Case3: current element is 1
else {
curr++;
}
}
}
//Explaination
/*
Aim: We want all the 0's on LHS of the array, and all the 2's on the RHS
of the array. This leaves the remaining 1's to be in the middle of array,
thus producing a sorted array.
Methodology:
To keep track of which elements in the array needs to be sorted, we use
3 cursors: low, curr, and high.
low: Tracks first index of the unsorted partition of array (initialised to 0)
High: Tracks last index of the unsorted partition of array (intilaised to last index of array)
curr: Tracks index of current unsorted element (initialised to 0)
Initially, the array is assumed to be unsorted. Hence low will be initialised to
the first index 0, high will be initialised to the last index of array, and curr
will be initialised to first index 0 as we sort elements left to right.
Now, if the current element is 0, then we want it on the LHS of the array.
Since the low cursor points to the first index of the unsorted
partition (LHS of array), we swap the current element with the element the
low cursor is pointing to. Now that we know 0 is in the correct side of the "sorted"
array, we decrease the size of the unsorted partition by incrementing the
low cursor. We also move on to sort the next element in array by incremeting
the curr cursor.
However, if the current element is 2, then we want it on the RHS of the array.
Since the high cursor points to the last index of the unsorted
partition (RHS of array), we swap the current element with the element the
high cursor is pointing to. Now that 2 is in the correct side of the "sorted"
array, we decrease the size of the unsorted partition by decrementing the
high cursor. However, unlike when our current element was a 0, we don't sort the next
element in the array by incrementing the curr cursor just yet. The reason is because
the element the high cursor was pointing to, now in curr's index, itself is
not guaranteed to be in the correct order.
For example, if we had the array
0 1 2 0 0, where low points to 1, curr points to 2, and high points to 0.
Since the current element is 2, then we need to swap it with the last index in
the unsorted partition which in this example is the second 0. This results
in an array of 0 1 0 0 2. But as you can see, the 0 we swapped 2 with, itself
is not correctly sorted as it comes after 1. So we have to consider sorting
the new current element of 0, and not the next element in array by incrementing just yet.
Now if the current element is 1, then we don't want to swap it with another element
so its on the LHS or RHS of the array. We want to leave it alone.
Thus, we just increment the curr cursor to sort the next element in the array.
This process repeats until the curr cursor passes the high cursor, as
anything to the right of the high cursor is guarenteed to be sorted from
previous sorts.
*/
characteristics
algorithms
mergesort re-merging process
(12)
// C code to implement quicksort
#include <stdio.h>
// Function to swap two elements
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
// Partition the array using the last element as the pivot
int partition(int arr[], int low, int high)
{
// Choosing the pivot
int pivot = arr[high];
// Index of smaller element and indicates
// the right position of pivot found so far
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than the pivot
if (arr[j] < pivot) {
// Increment index of smaller element
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
// The main function that implements QuickSort
// arr[] --> Array to be sorted,
// low --> Starting index,
// high --> Ending index
void quickSort(int arr[], int low, int high)
{
if (low < high) {
// pi is partitioning index, arr[p]
// is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Driver code
int main()
{
int arr[] = { 10, 7, 8, 9, 1, 5 };
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
quickSort(arr, 0, N - 1);
printf("Sorted array: \n");
for (int i = 0; i < N; i++)
printf("%d ", arr[i]);
return 0;
}
// Heap Sort in C
#include <stdio.h>
// Function to swap the position of two elements
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// To heapify a subtree rooted with node i
// which is an index in arr[].
// n is size of heap
void heapify(int arr[], int N, int i)
{
// Find largest among root,
// left child and right child
// Initialize largest as root
int largest = i;
// left = 2*i + 1
int left = 2 * i + 1;
// right = 2*i + 2
int right = 2 * i + 2;
// If left child is larger than root
if (left < N && arr[left] > arr[largest])
largest = left;
// If right child is larger than largest
// so far
if (right < N && arr[right] > arr[largest])
largest = right;
// Swap and continue heapifying
// if root is not largest
// If largest is not root
if (largest != i) {
swap(&arr[i], &arr[largest]);
// Recursively heapify the affected
// sub-tree
heapify(arr, N, largest);
}
}
// Main function to do heap sort
void heapSort(int arr[], int N)
{
// Build max heap
for (int i = N / 2 - 1; i >= 0; i--)
heapify(arr, N, i);
// Heap sort
for (int i = N - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]);
// Heapify root element
// to get highest element at
// root again
heapify(arr, i, 0);
}
}
// A utility function to print array of size n
void printArray(int arr[], int N)
{
for (int i = 0; i < N; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver's code
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
heapSort(arr, N);
printf("Sorted array is\n");
printArray(arr, N);
}
// This code is contributed by _i_plus_plus_.
// C program for insertion sort
#include <math.h>
#include <stdio.h>
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
}
/* Driver program to test insertion sort */
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}
// Optimized implementation of Bubble sort
#include <stdbool.h>
#include <stdio.h>
void swap(int* xp, int* yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
int i, j;
bool swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(&arr[j], &arr[j + 1]);
swapped = true;
}
}
// If no two elements were swapped by inner loop,
// then break
if (swapped == false)
break;
}
}
// Function to print an array
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
}
// Driver program to test above functions
int main()
{
int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
int n = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
if(min_idx != i)
swap(&arr[min_idx], &arr[i]);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
| Selection Sort | Ω(n^2) | θ(n^2) | O(n^2) |
| Bubble Sort | Ω(n) | θ(n^2) | O(n^2) |
| Insertion Sort | Ω(n) | θ(n^2) | O(n^2) |
| Heap Sort | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) |
| Quick Sort | Ω(n log(n)) | θ(n log(n)) | O(n^2) |
| Merge Sort | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) |
Types Of Time Complexity :
Ways to Determine the Difference Between Sorting Algorithms:
1) Time Complexity
2) Stability (Stable: Bubble Sort, Insertion Sort and Merge Sort) (Unstable: Vanilla Qsort, Qsort, MoT, Randomised QSort, Shell Sort, Powers of Four)
3) Bubble Sort Ascending with Early Exit would have ascending input sets be the fastest in all cases.
4) Merge Sort divides the list regardless of the order, so it is input agnostic.
5) For descending inputs, insertion sort will take longer than most other sorts, as with descending inputs, the final sorted list will need to be incrementally moved
6) Quicksort similarly has this issue, but we know that there is a difference in stability.
7) Obviously - randomised qsort will be input agnostic
Invalid message: Your post must contain text!