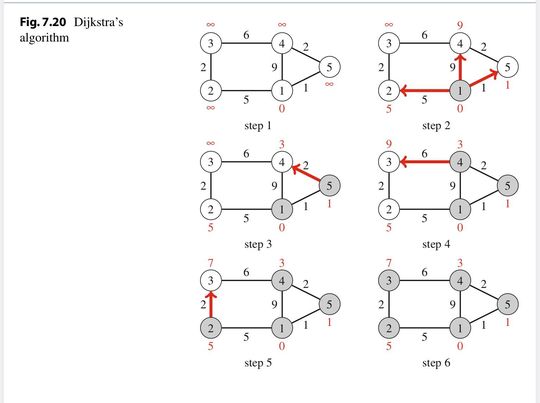
Annotated the lecture slides + added some stuff



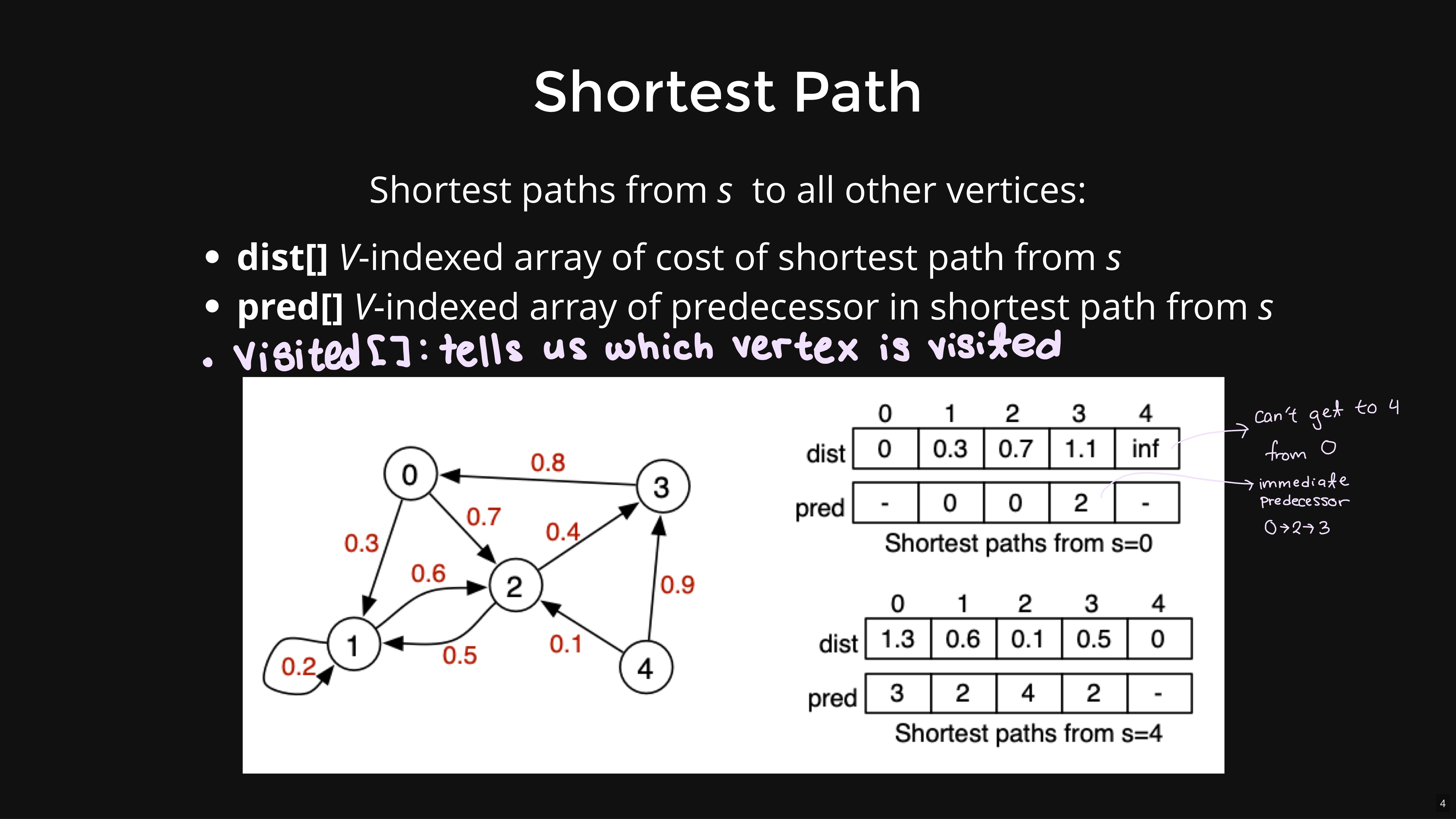

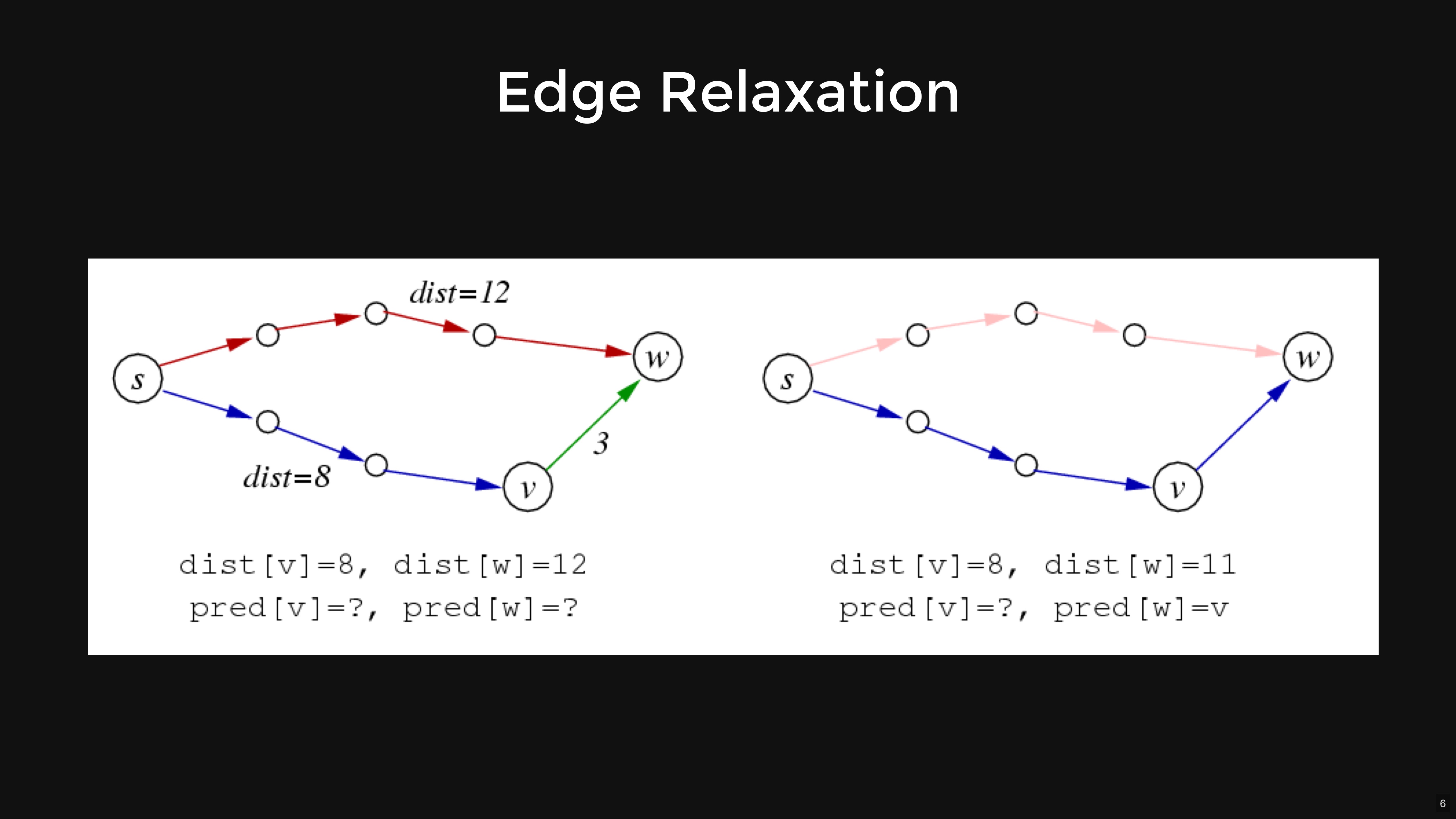


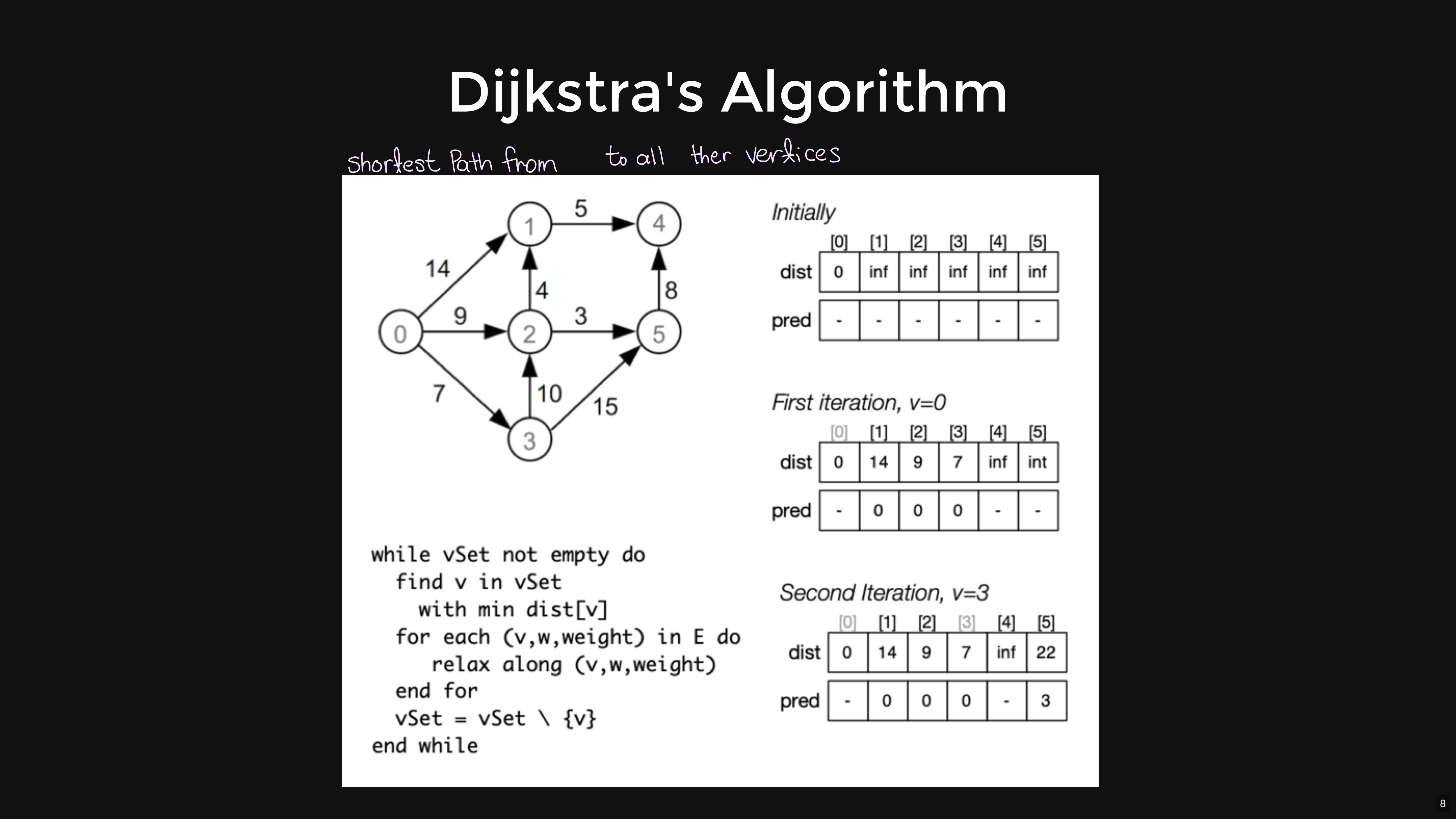

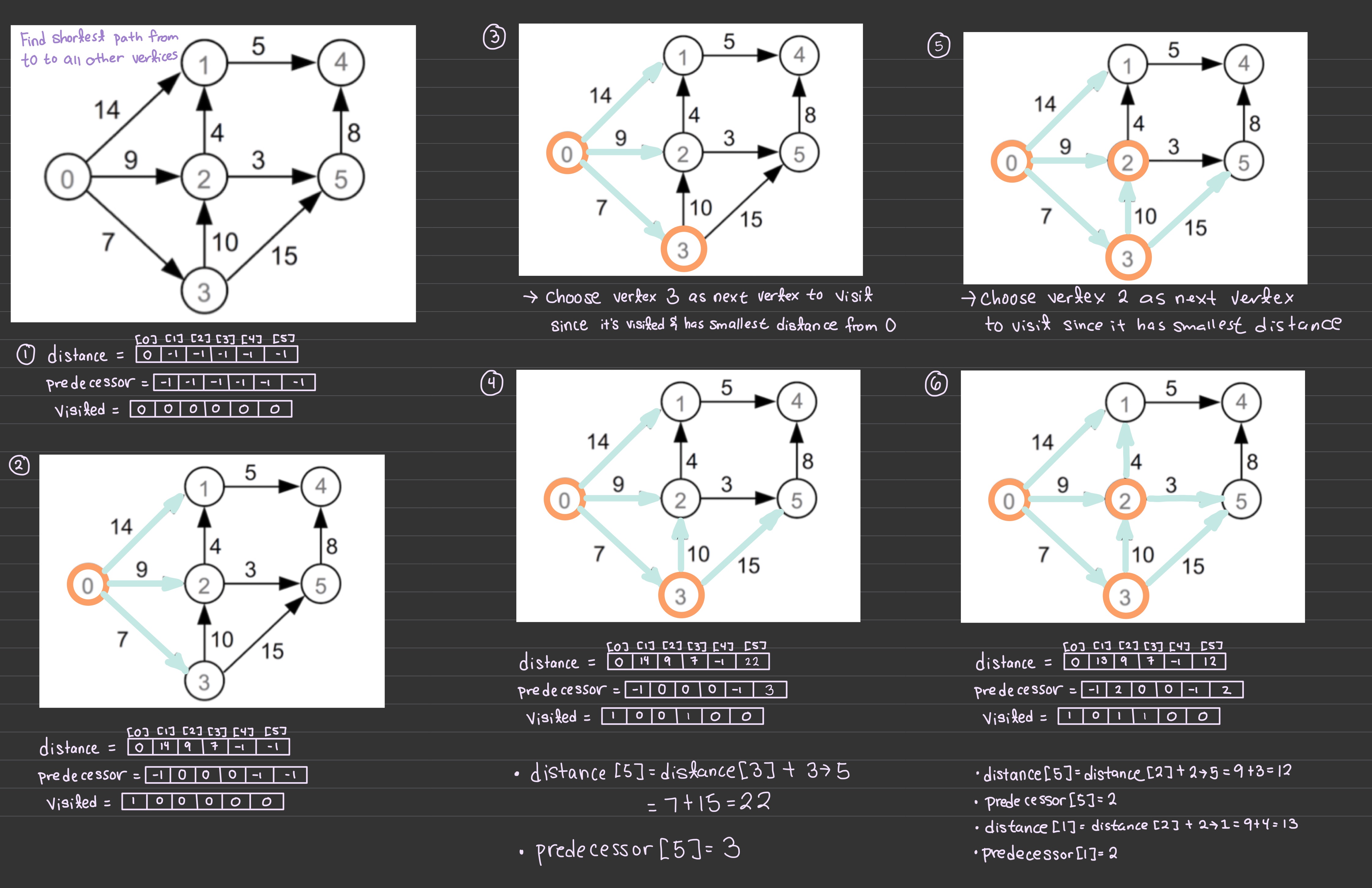
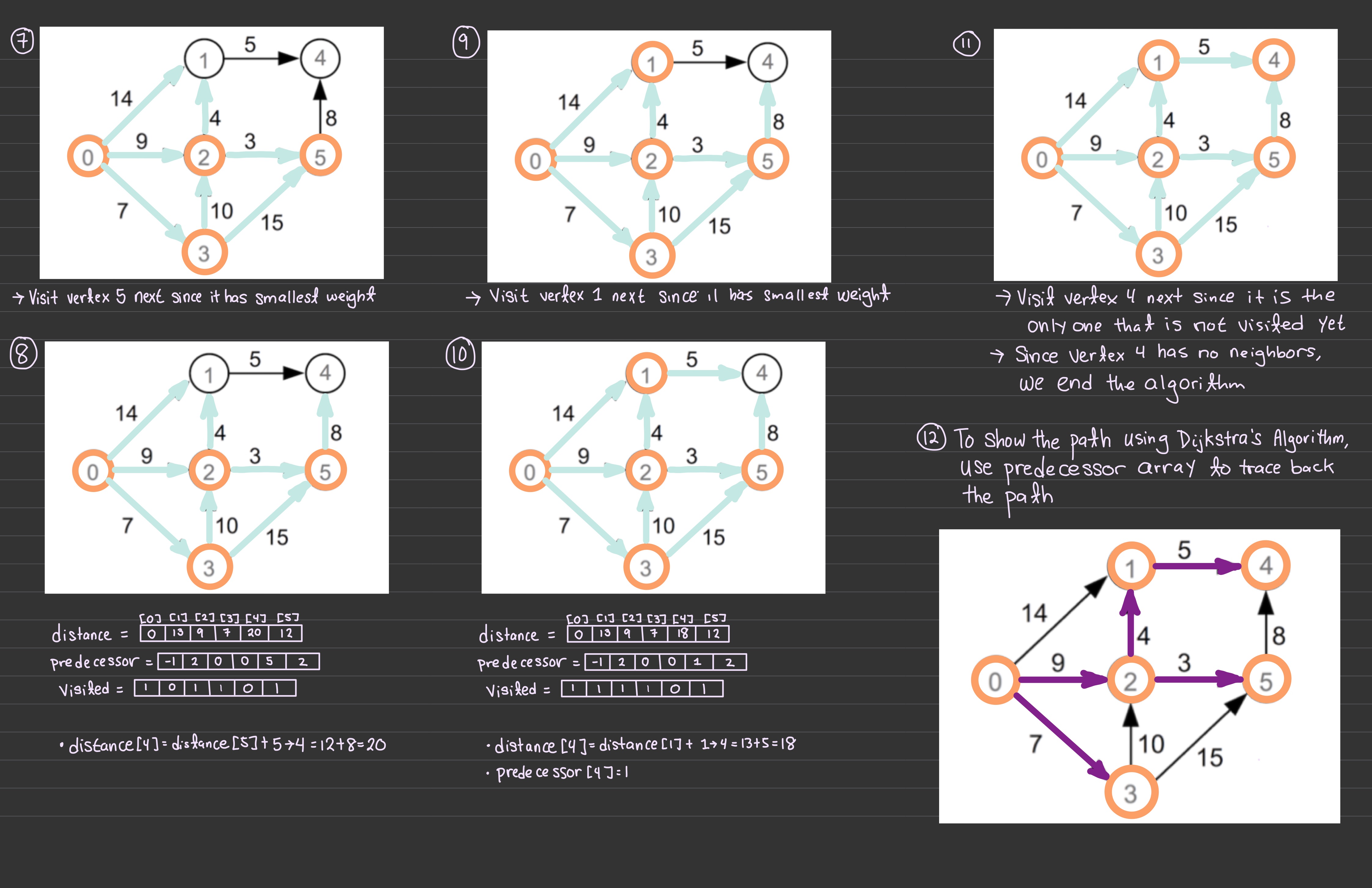

dijkstraSSSP(G, source):
dist[] // array of cost of shortest path from s
pred[] // array of predecessor in shortest path
// from s
vSet // vertices whose shortest path from s is
// unknown
initialise all dist[] to infinity/-1
dist[source] = 0
initialise all pred[] to -1
vSet = all vertices of G
while vSet is not empty:
find v in vSet with minimum dist[v]
for each (v, w, weight) in G->edges:
relax along (v, w, weight)
vSet = vSet \ {v}
Annotated the lecture slides + added some stuff













Dijkstra's Algorithm
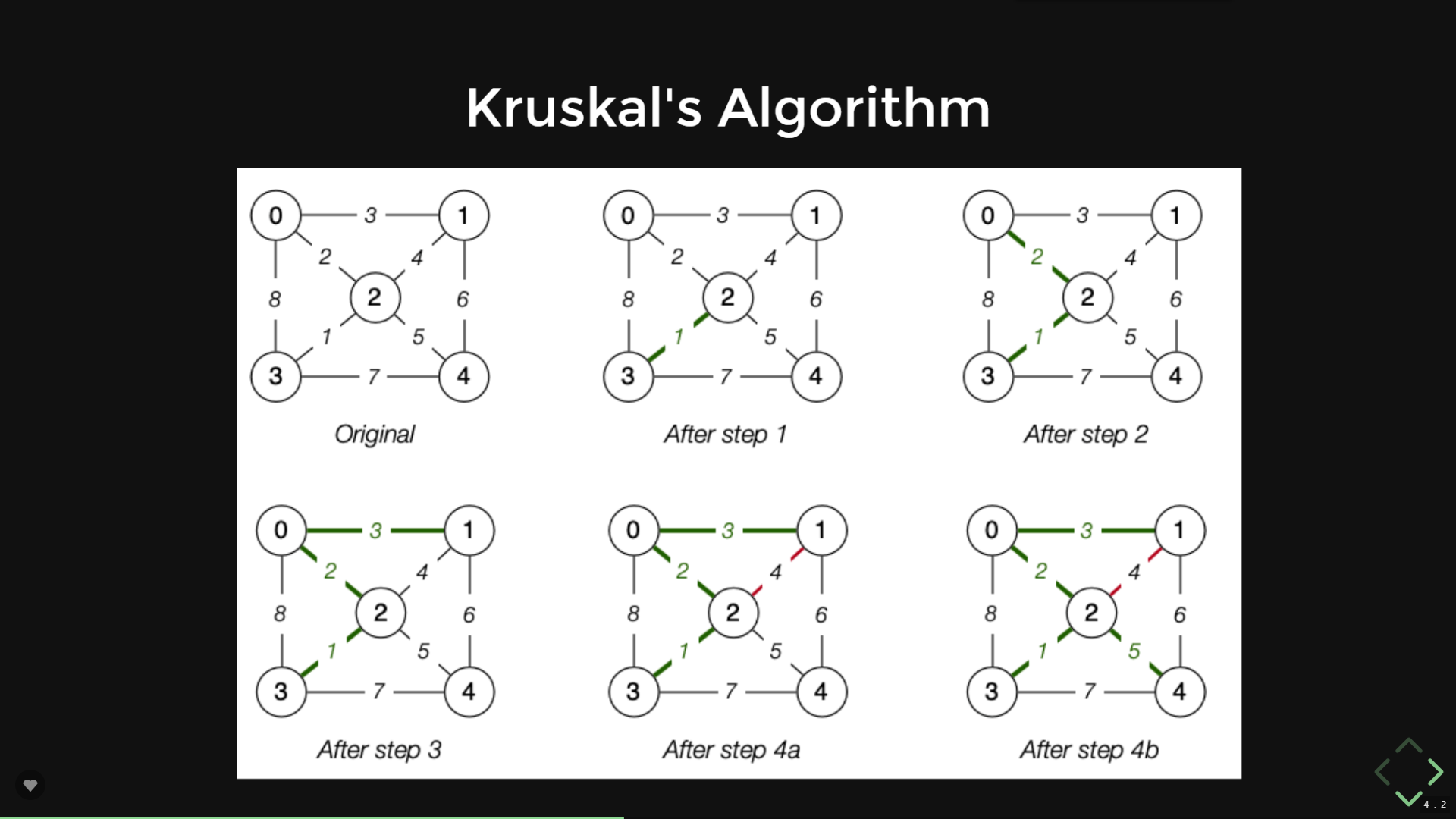
Kruskal's Algorithm
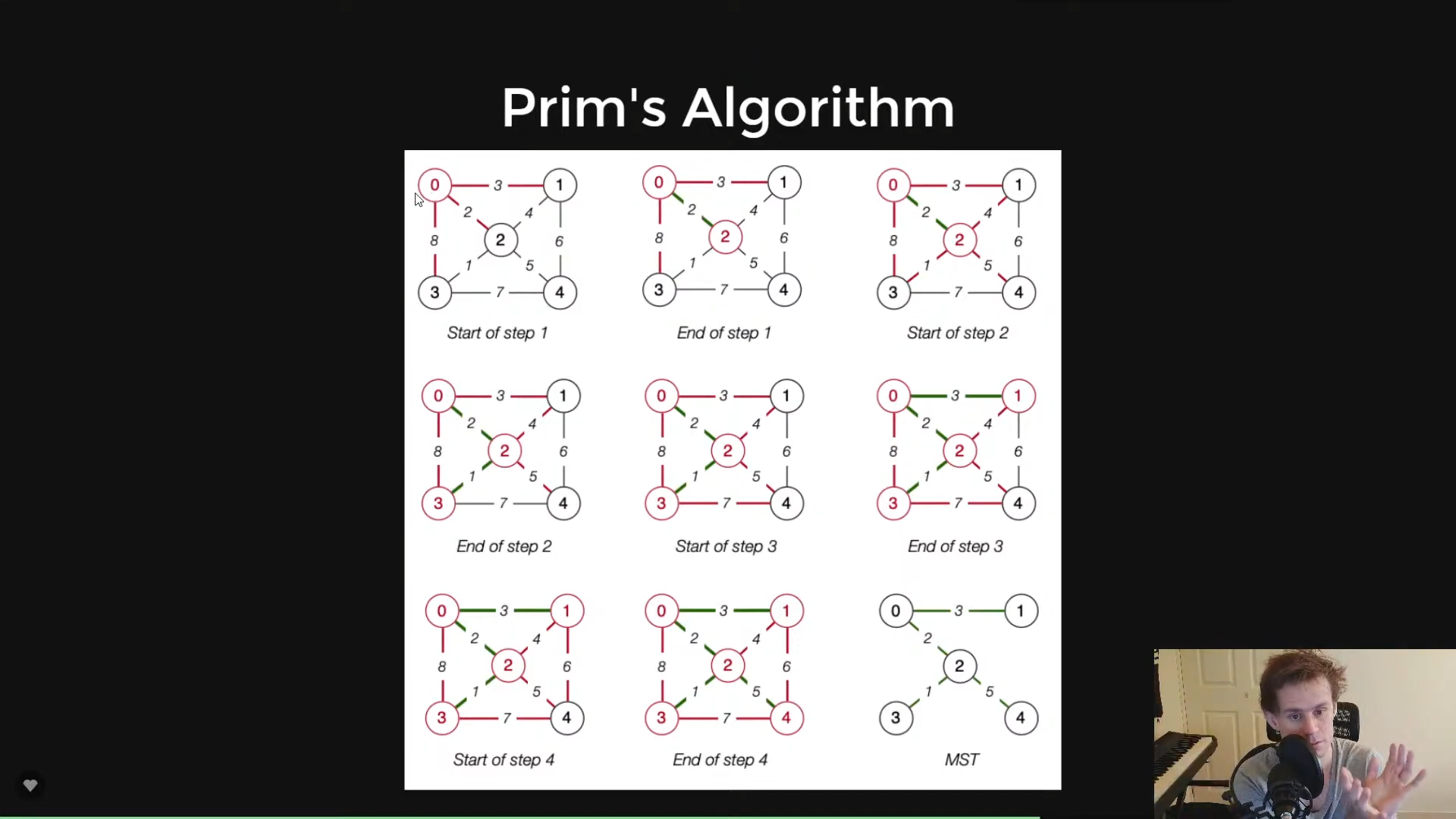
Prime's Algorithm
int shortestDistance(Graph g, int src, int dest) {
// Standard BFS
int nV = GraphNumVertices(g);
int pred[nV];
for (int i = 0; i < nV; i++) {
pred[i] = -1;
}
pred[src] = src;
bool found = false;
Queue q = QueueNew();
QueueEnqueue(q, src);
while (!found && !QueueIsEmpty(q)) {
int v = QueueDequeue(q);
for (int w = 0; w < nV; w++) {
if (GraphIsAdjacent(g, v, w) && pred[w] == -1) {
pred[w] = v;
if (w == dest) {
found = true;
}
QueueEnqueue(q, w);
}
}
}
QueueFree(q);
if (pred[dest] == -1) {
return -1;
}
int distance = 0;
while (dest != src) {
distance++;
dest = pred[dest];
}
return distance;
}