Recursion

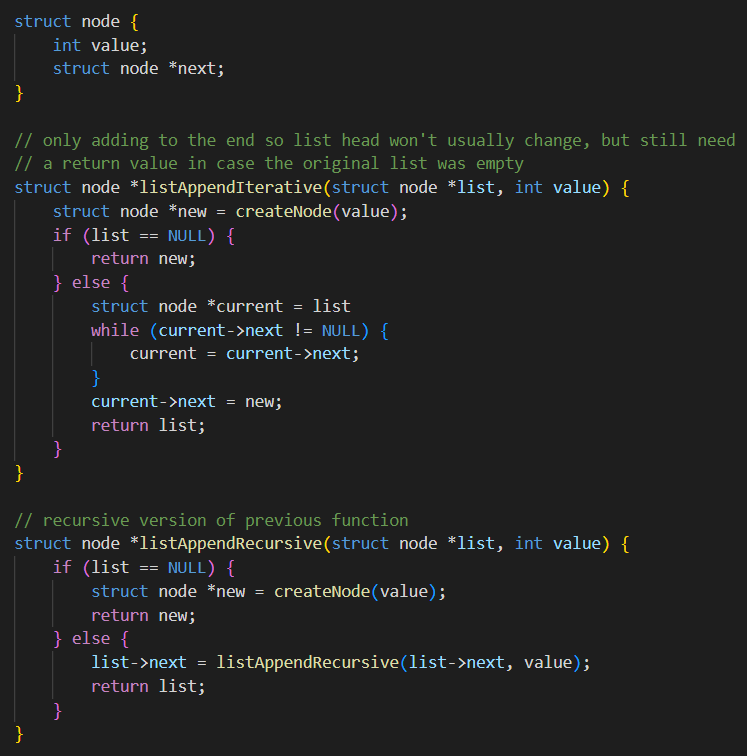
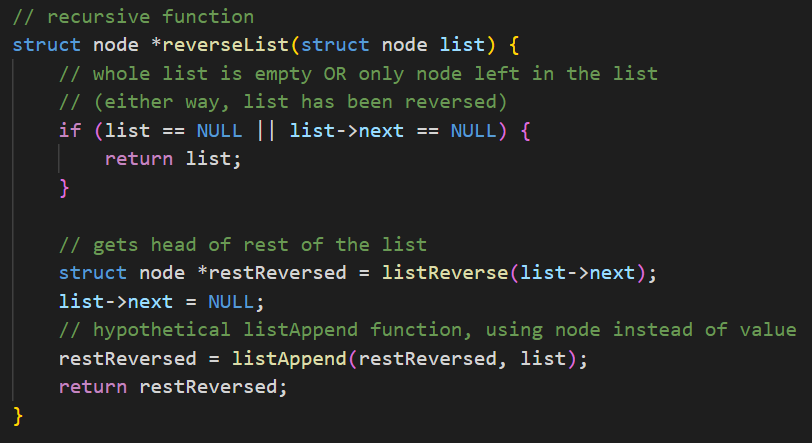
listTail:

check if list next is NULL, if it is return the current node

else, recurse next value.

listMax:

if list next = NULL, return current value

else: initialise max to the recursed called next value

if the current value greater than max, return the current one, otherwise

return max

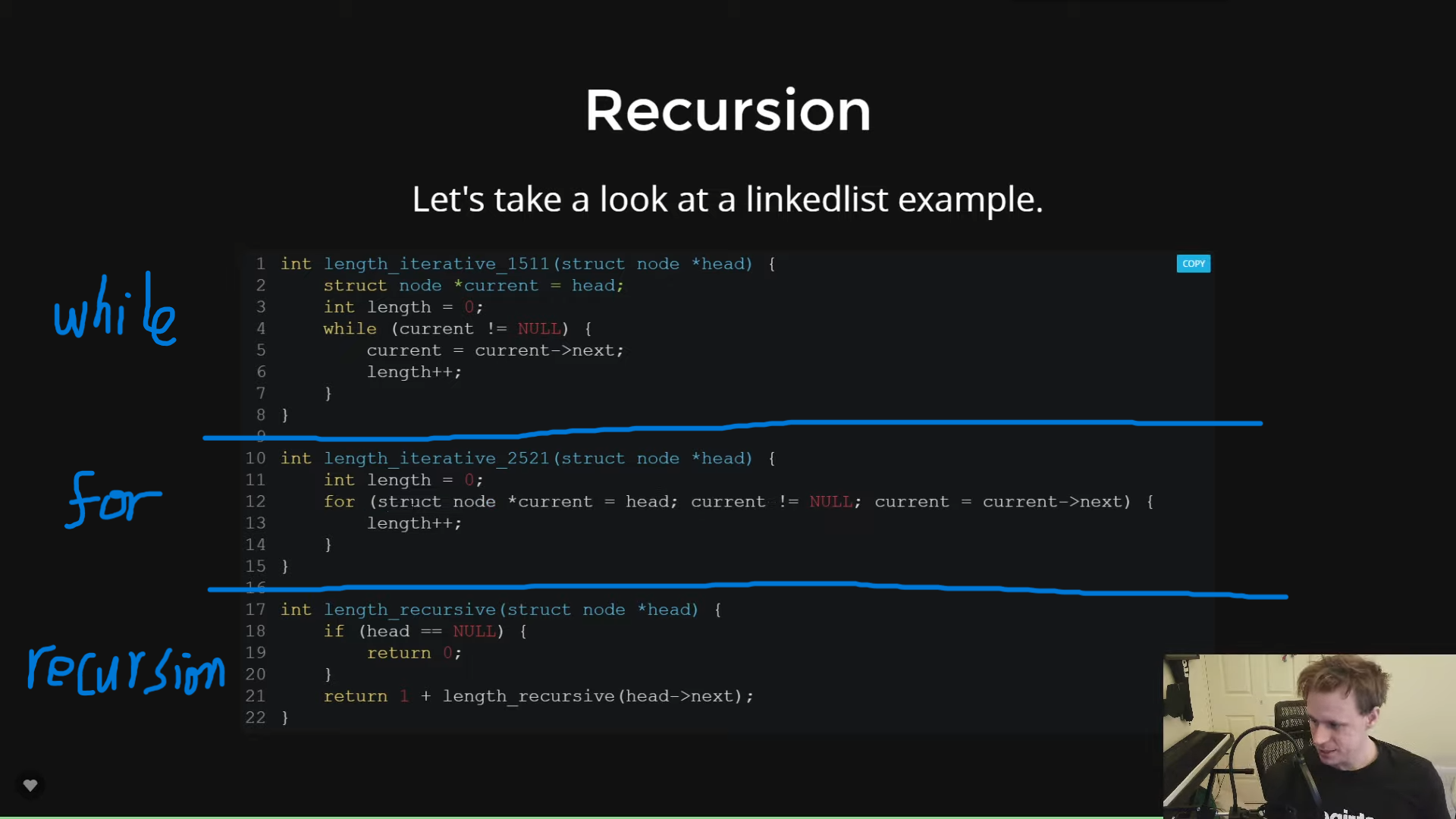
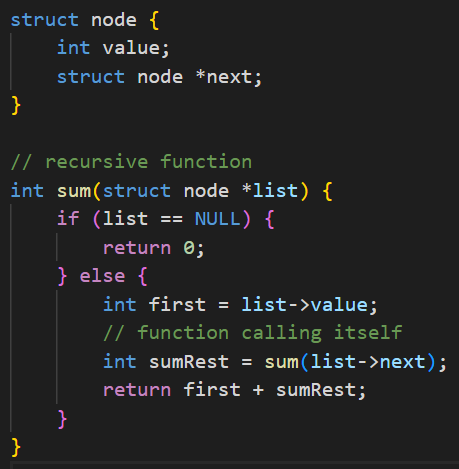
listSum:

if list is null, return 0;

else; return the current value + helper(next).

listInsertOrdered:

if the head is null, or the value is less than head value:

create newnode, newnode next is head, return n;

else: head->next is the recurse call of the next value
return the head.

listInsertNth:

if head is null, or n <= 0:

create a newnode,

make the newnode point to head, return the newnode.
else {

make the head point to the recursed call of the next node

return head;

example

Summing all elements in an array:

#include <stdio.h>
int recursiveSum(int arr[], int size, int index) {
    // Base case: If the array is empty or has only one element, return its value
    if (index == size - 1) {
        return arr[index];
    }
    // Recursive case: Calculate the sum of the current element and the remaining elements
    int currentSum = arr[index];
    int remainingSum = recursiveSum(arr, size, index + 1);
    return currentSum + remainingSum;
}
int main() {
    int arr[] = {1, 2, 3, 4, 5};
    int size = sizeof(arr) / sizeof(arr[0]);
    int totalSum = recursiveSum(arr, size, 0);
    printf("Sum of array elements: %d\n", totalSum);
    return 0;
}

Reversing an array:

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}
void reverseArray(int arr[], int start, int end) {
    // Base case: If the array is empty or has only one element, return
    if (start >= end) {
        return;
    }
    // Swap the first and last elements
    swap(&arr[start], &arr[end]);
    // Recursively reverse the subarray excluding the first and last elements
    reverseArray(arr, start + 1, end - 1);
}

Finding an element in an array:

int doesElementExist(int arr[], int size, int target, int index) {
    // Base case: If the index goes out of bounds, the element is not found
    if (index >= size) {
        return 0;
    }
    // Base case: If the current element matches the target, return true
    if (arr[index] == target) {
        return 1;
    }
    // Recursively search for the element in the remaining part of the array
    return doesElementExist(arr, size, target, index + 1);
}

int pow(int x, unsigned int n) { 
    if (n == 0) return 1; 
    if (n == 1) return x; 
    if (n % 2 == 0) { // n is even 
        return pow(x * x, n / 2); 
    } else { // n is odd 
        return x * pow(x * x, n / 2); 
    } 
}

struct node *listDelete(struct node *l, int value) { 
    if (l == NULL) { 
        return NULL; 
    } else if (l->value == value) { 
        struct node *restOfList = l->next; 
        free(l); 
        return restOfList; 
    } else { 
        l->next = listDelete(l->next, value); 
        return l; 
    } 
}

A recursive function is made of two components:

1) Base case: the condition when the recursion ends and the function ceases to call itself again. Because a recursive function calls itself, it is easy to write a function incorrectly that ends up in an infinite loop. Without a base case to end the recursion, the function will run forever (or until the program crashes/is stopped).

2) Recursive call. The recursive case is when the function calls itself — over and over again with a smaller portion of the initial input.

• recursion
  • can often do same thing with loops, but recursion makes it quicker/easier to code (but uses lots of memory)
  • doing one function/’loop’, then delegating → each time the function is called, it does some of the work + then calls the function again, repeating until there’s no more work to do
• terminology:
  • base case = when to stop calling function
  • recursive case = more to be done, recursion keeps going (function called again)

example: sum of list of numbers

• loops: adding each number one by one → while/for loop, adding to single variable each time

VS.

• recursion: each loop, current number plus [sum of rest of list] until [sum of rest of list = 0]

other examples:

examples using lists: