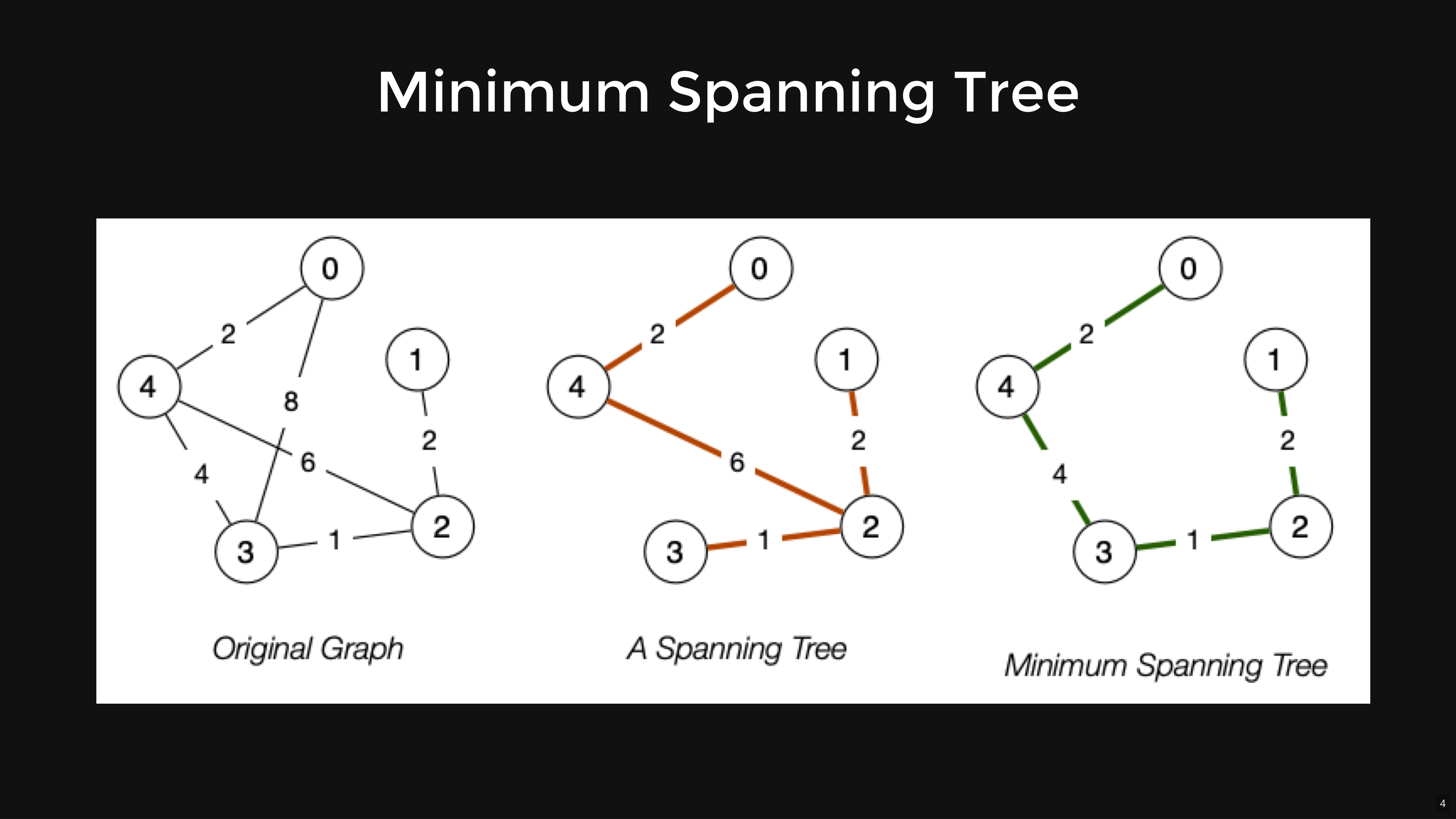
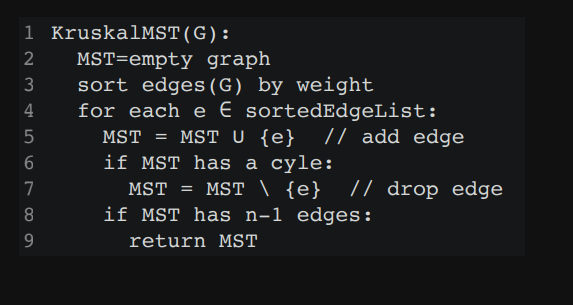
MSTs:
// Kruskal Pseudocode
KruskalMST(G) {
int n = number of vertices in G;
Edge MST[n-1];
Edge sortedEdgeList[] = edges(G);
int unionFind[n];
for (int i = 0; i < n; i++) unionFind[i] = i;
qsort(sortedEdgeList, m, sizeof(Edge), compareEdges);
int count = 0;
int i;
for (i = 0; i < m && count < n-1; i++) {
Edge e = sortedEdgeList[i];
int u = find(e.s, unionFind);
int v = find(e.t, unionFind);
if (u != v) MST[count++] = e, unionFind[u] = v;
}
if (count == n-1) return MST;
else /* Handle error */;<span class="redactor-invisible-space"></span>
Complexity Breakdown
Minimum Spanning Tree Lecture Slides Annotated
Annotated lecture slides + added some stuff
MST implement
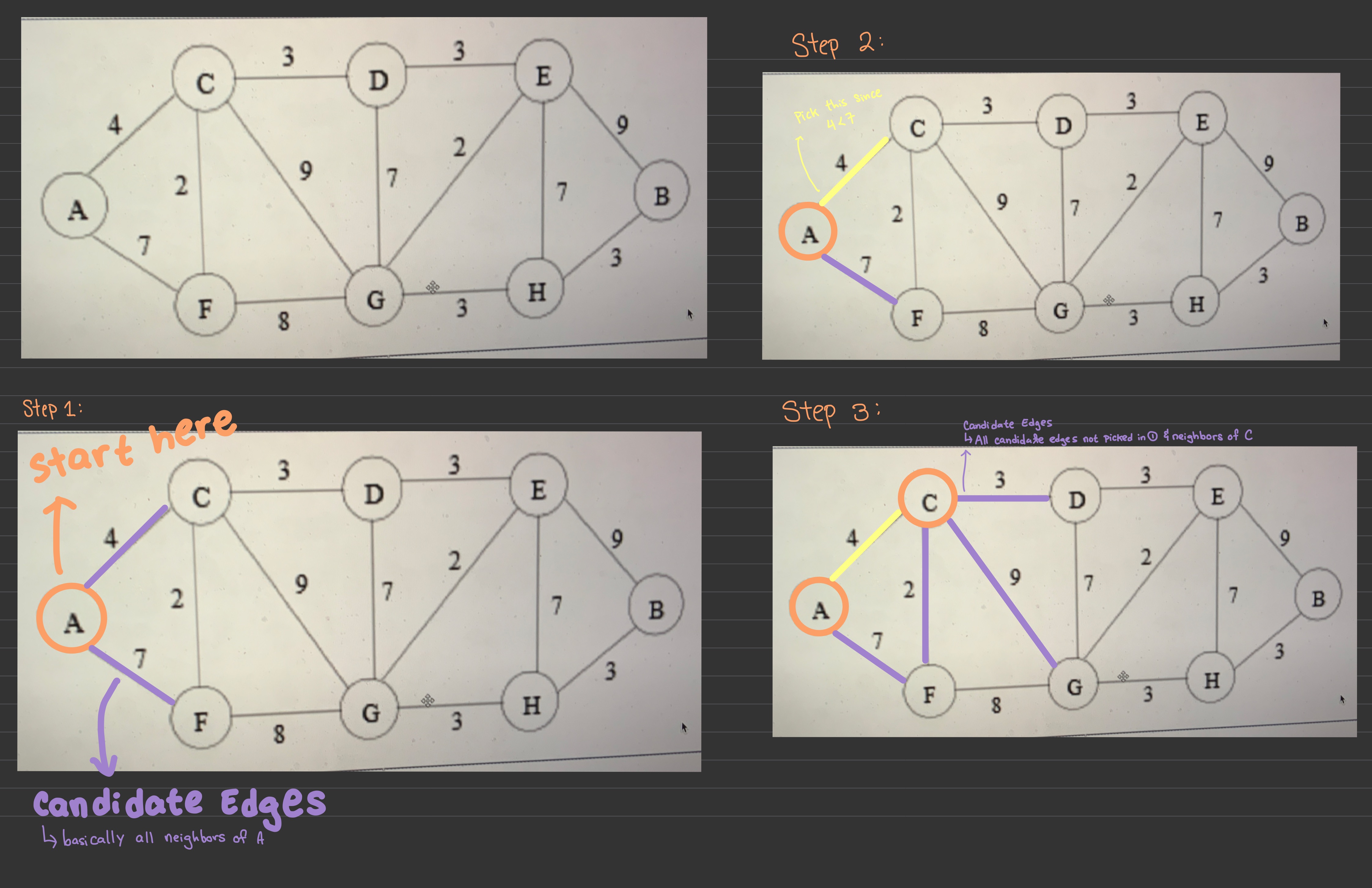
if graph has cycle, return NULL
new graph with number of edges as vertex number
new priority queue
for loop i < original graph's num of vertex
for loop j < original graph's num of vertex
if graph->edges[i][j] != 0
initialise new edge
edge.v = i
edge.w = j
edge's weight = graph's edges[i][j]
insert edge to priority queue
end if
end for loop j
end for loop i
while(newgraph(mst) < original graph's num of vertex - 1
edge = priority queue extract
insert the edge in newMstGraph
if newMstGraph has cycle
remove edge
end if
end while
free priority queue
return newMstGraph
Graph has cycle?
bool visited array with size of graph's num of vertex
for loop v < # of vertex in graph
if v is not visited && doHasCycle(g,v,v,visited)
free visited array and return true
end if
end for
free visited array and return false
doHasCycle (graph, vertex v and prev , bool visited array)
set v visited as true
for w < # of vertex in graph
if graph edges [v][w] != 0.0
if w is not visited
if doHasCycle(g,w,v,visited)
return true
end if
else if w is not prev
return true
end else if
end if
end for loop
return false
Dijkstra's algorithm VS Kruskal's algorithm
differences
Kruskal's algorithm pseudocode
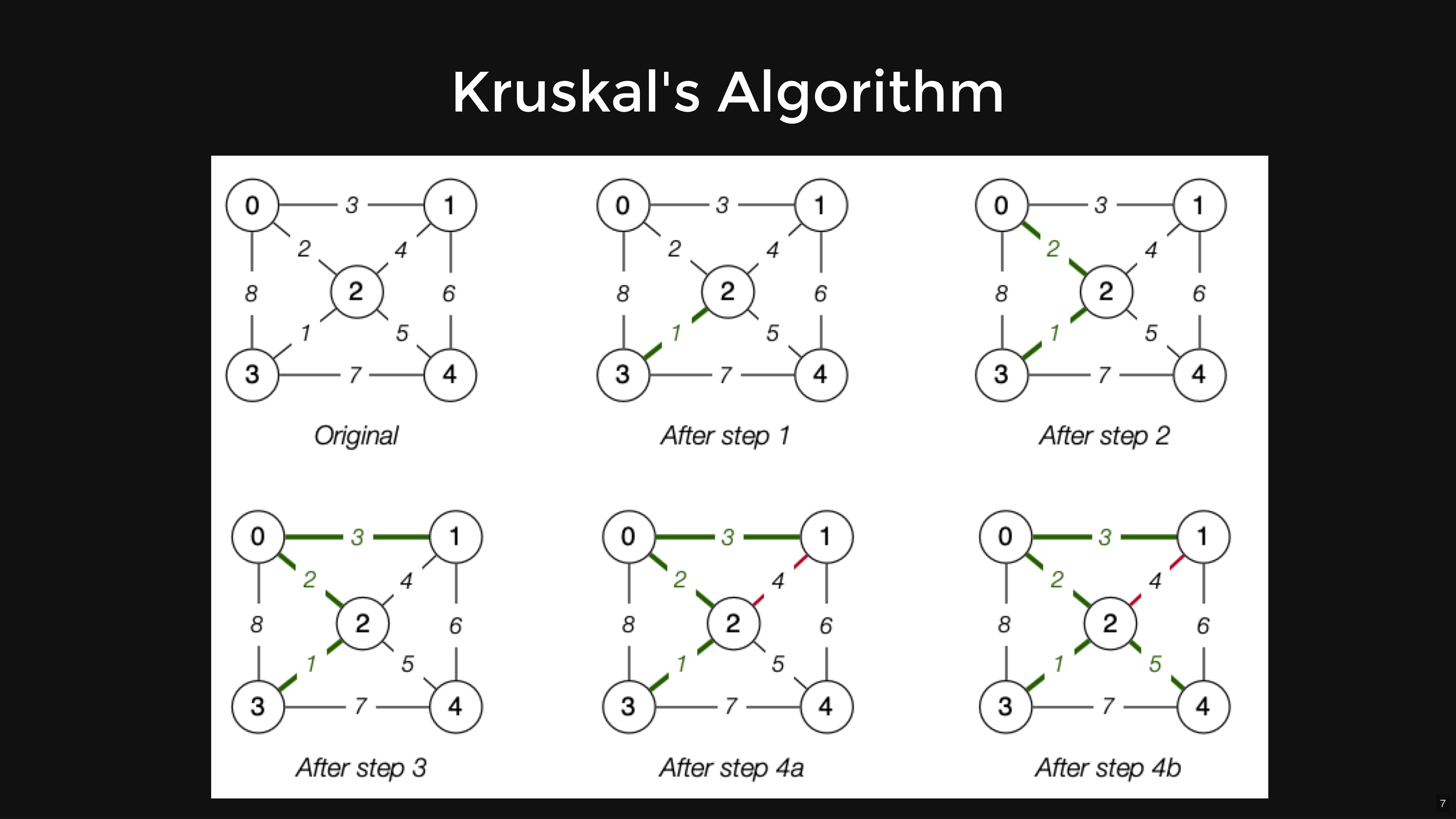
Kruskal's algorithm pseudocode
Example of C Implementation:
Graph KruskalMST(Graph G) {
MST = GraphNew(G->numVert);
struct edge *sortedEdges = malloc(sizeof(struct edge) * G->numEdges);
sortEdgesWeight(G, sortedEdges); \\ Helper function to implement
for (int i = 0; i < G->numEdges; i++) {
MST = insertEdge(MST, sortedEdges[i]);
if(hasCycle(MST)) { \\ Helper function to implement (Depth First Search can help)
MST = removeEdge(MST, sortedEdges[i])
}
if(MST->numEdges = MST->numVert - 1) {
return MST;
}
}
}
Notes:
Creating MST involves gathering the lowest valued edges while eliminating edges that create loops/cycles. Can be unreliable as it may return a disconnected graph (not all nodes are reachable from some given node). It can be checked if this has been completed by a DFS across all nodes to see if every node is accessible, however, this is generally time costly. Prim's algorithm is a good alternative in this case as it only assesses edges to be added to MST if one of its nodes has already been visited.
insertion sort pseudocode (e.g. struct road sort)
start for loop i = 1 & i < array size
struct road r = array[i]
int j is same with i
start while loop when j is greater than 0 AND r's value is smaller than array[j-1]'s value
array[j] = array[j-1]
decrease index j
end while loop
array[j] is set by r
end for loop
Prim's pseudocode
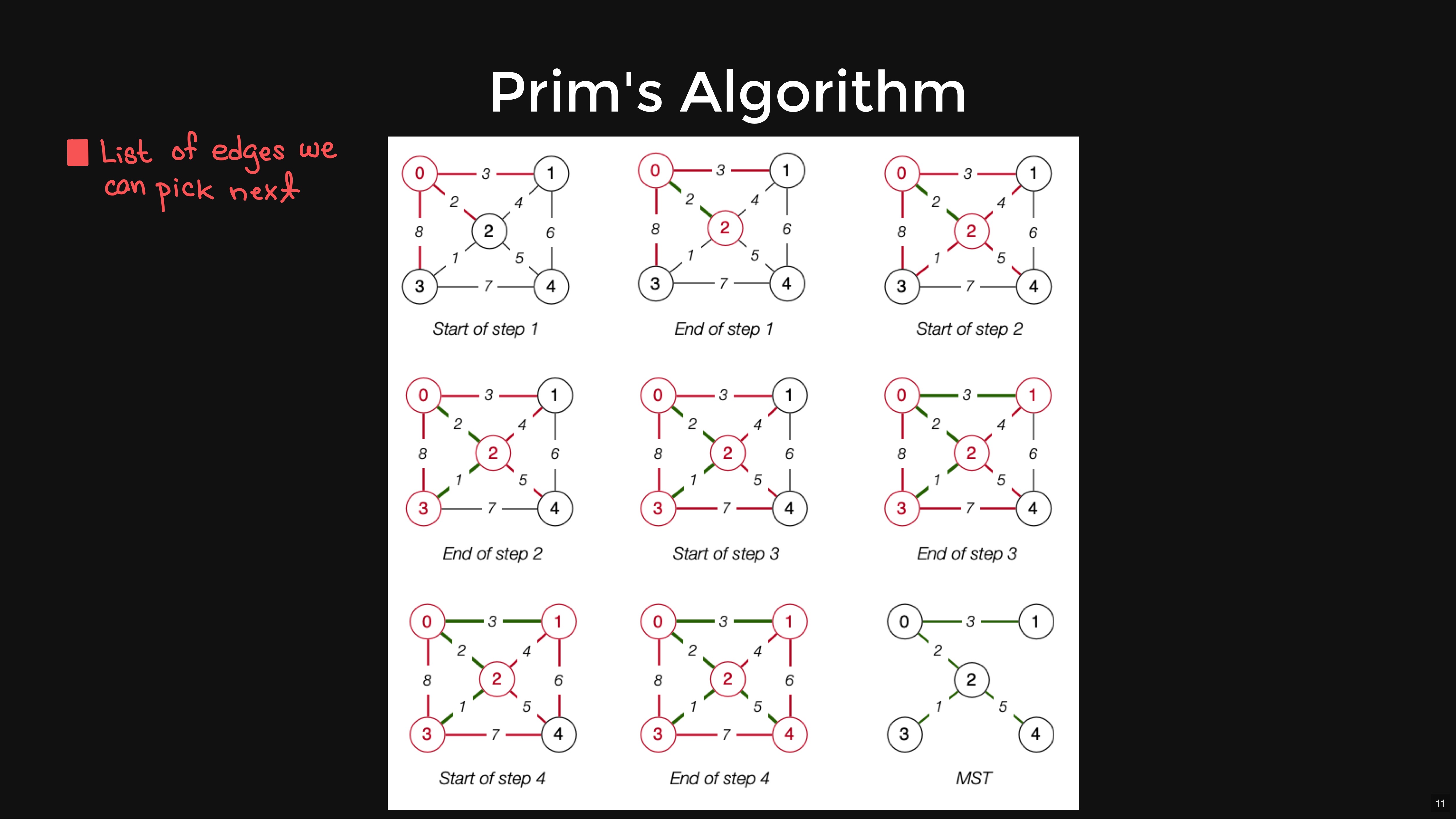
PrimMST(G) {
int n = number of vertices in G;
Edge MST[n-1];
bool usedV[n];
Edge unusedE[] = edges(G);
usedV[0] = true;
int count = 0;
int i;
while (count < n-1) {
Edge e;
int minWeight = INT_MAX;
for (i = 0; i < m; i++) {
if (usedV[unusedE[i].s] && !usedV[unusedE[i].t] && unusedE[i].w < minWeight) {
e = unusedE[i];
minWeight = unusedE[i].w;
}
}
MST[count++] = e;
usedV[e.t] = true;
unusedE[i] = unusedE[--m];
}
return MST;
}
DetectCycle code
bool graphDetectCycle(Graph g) {
bool hasCycle = false;
// declare visited array
bool visited[MAX_NUM_VERTICES] = {};
// declare stack and initialise with first node
int toVisitStack[4*MAX_NUM_VERTICES] = {};
toVisitStack[0] = 0;
int stackTop = 1;
while (!hasCycle && stackTop > 0) {
int node = toVisitStack[--stackTop];
if (!visited[node]) {
visited[node] = true;
for (int otherNode = 0; otherNode < numVertices(g); otherNode++) {
if (otherNode == node || !adjacent(g, node, otherNode)) {
continue;
}
// printf("Checking %d's neighbour %d\n", node, otherNode);
if (!visited[otherNode]) {
if (stackHasNode(toVisitStack, stackTop, otherNode)) {
// If we plan to visit a node that we already planned
// to visit from a different node, we have a cycle.
hasCycle = true;
break;
} else {
// Neighbour has not been visited yet and there is
// presently no plan to visit it - make a plan
// to visit it.
toVisitStack[stackTop++] = otherNode;
}
}
}
}
}
return hasCycle;
}
bool stackHasNode(int stack[], int stackSize, int node) {
for (int i = 0; i < stackSize; i++) {
if (stack[i] == node) {
return true;
}
}
return false;
}
Cycle check Psedocode
for cycle check:
bool visited
for loop:
if unvisited and has cycle(g,v,v,visited):
free(visited) && return;
has cycle? :
visited = true;
for loop(nV):
if (adjcent) {
if(visited) {
if (w != pre) ->> TRUE;
} else {
if(has cycle?(g,w,v,visited)) ->> TRUE;
}
}
return F;
Prim's vs Kruskal's
| Prim's Algorithm | Kruskal's Algorithm | ||
| It starts to build the Minimum Spanning Tree from any vertex in the graph. | It starts to build the Minimum Spanning Tree from the vertex carrying minimum weight in the graph. | ||
| It traverses one node more than one time to get the minimum distance. | It traverses one node only once. | ||
| Prim’s algorithm has a time complexity of O(V2), V being the number of vertices and can be improved up to O(E log V) using Fibonacci heaps. | Kruskal’s algorithm’s time complexity is O(E log V), V being the number of vertices. | ||
| Prim’s algorithm gives connected component as well as it works only on connected graph. | Kruskal’s algorithm can generate forest(disconnected components) at any instant as well as it can work on disconnected components | ||
| Prim’s algorithm runs faster in dense graphs. | Kruskal’s algorithm runs faster in sparse graphs. | ||
| It generates the minimum spanning tree starting from the root vertex. | It generates the minimum spanning tree starting from the least weighted edge. | ||
| Applications of prim’s algorithm are Travelling Salesman Problem, Network for roads and Rail tracks connecting all the cities etc. | Applications of Kruskal algorithm are LAN connection, TV Network etc. | ||
| Prim’s algorithm prefer list data structures. |
|
Kruskal’s or Prim’s algorithm, what cases should one be used over another for creating a minimal spanning tree?
the time complexity of Prim’s algorithm is O(V^2) and the time complexity of Kruskal’s algorithm is O(E log V). So for a sparse graph (lots of vertices but few edges), Kruskal’s is faster, but if you have a much more dense graph, then Prim’s is quicker
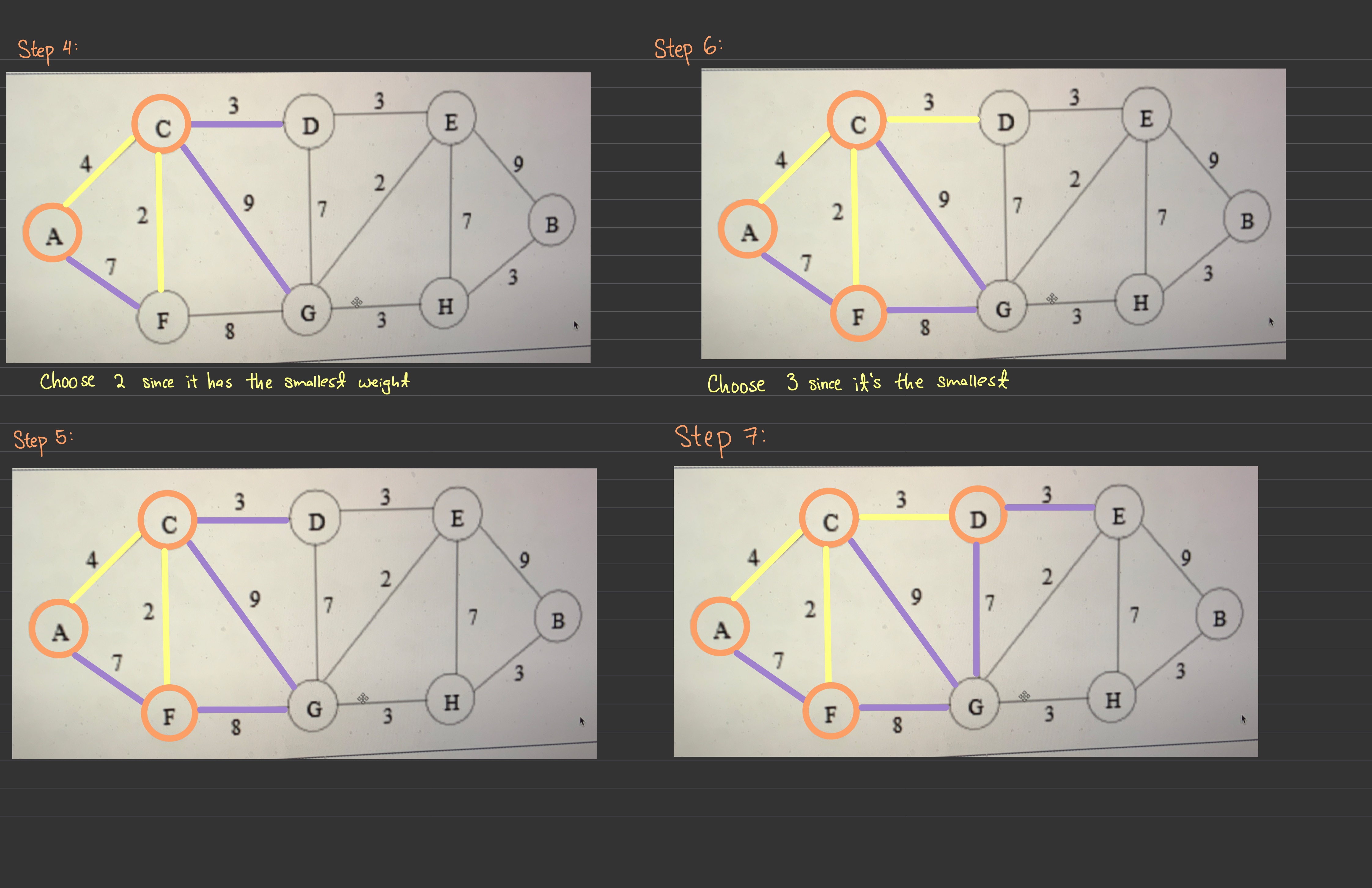
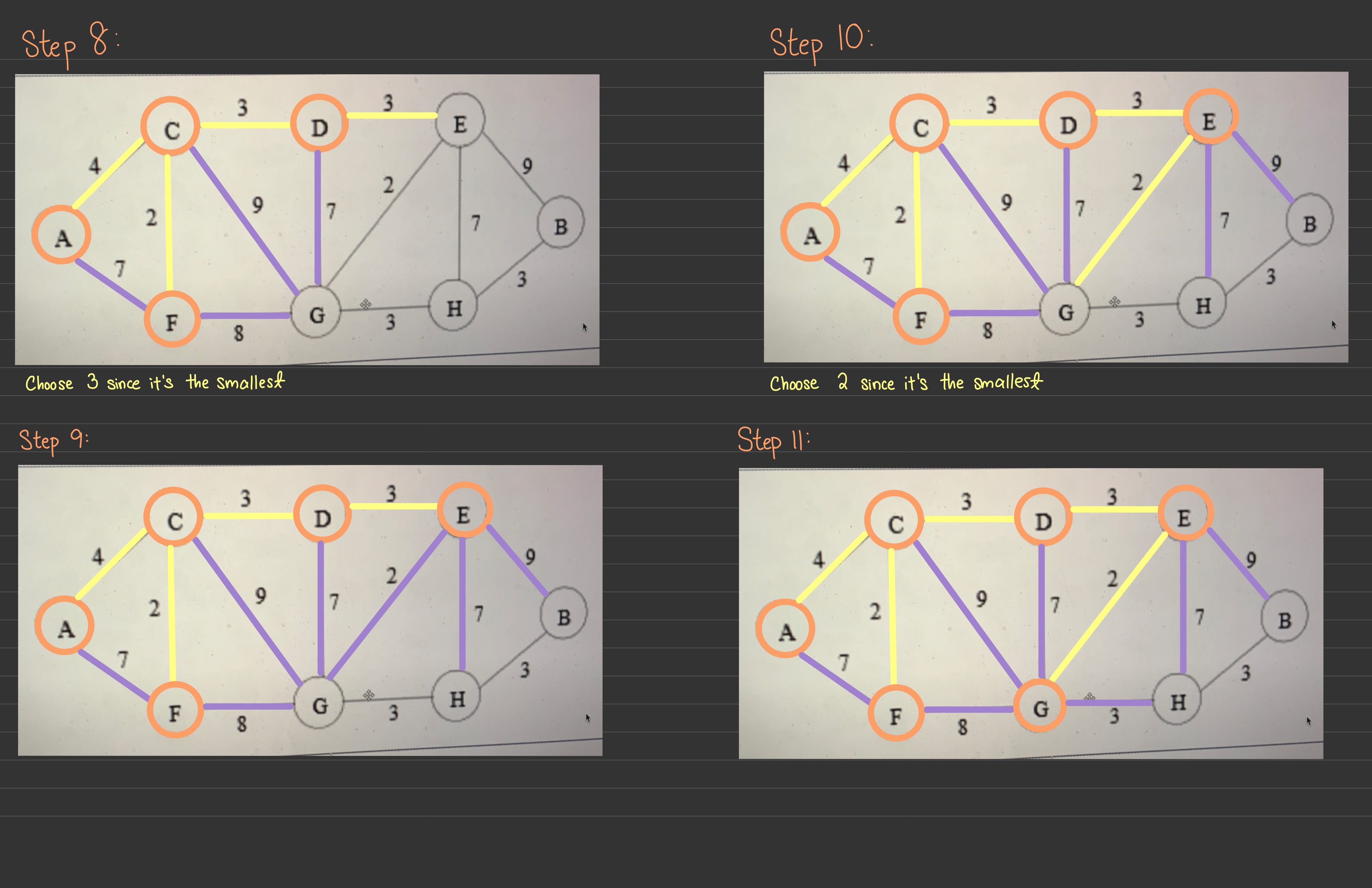
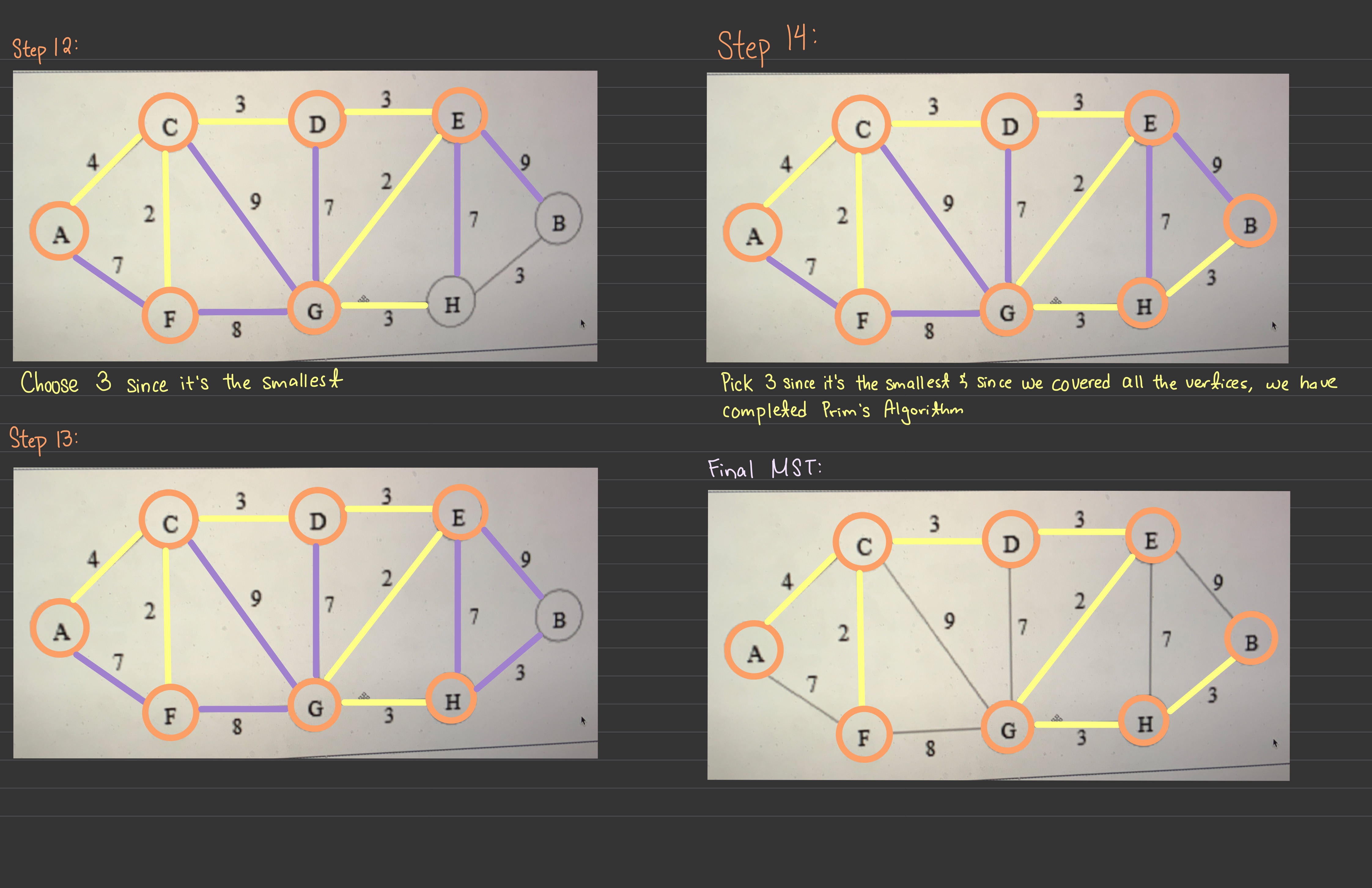
During the execution of Prim's algorithm, every new edge added to the MST must be connected to the edges that have already been added. E.g. for this graph
A-E
E-C
C-D
etc..