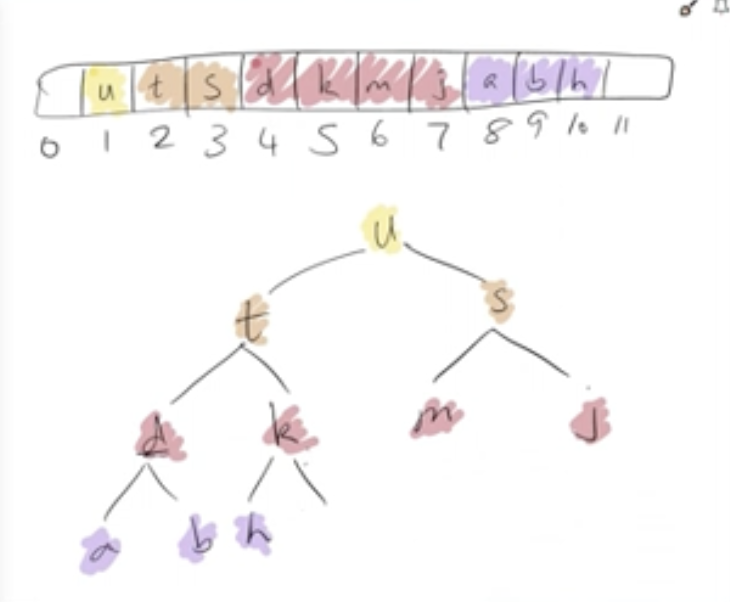
deleting process in heap

Heap insertion

Heap Structure:

Simple index calculations allow navigation through the tree:

- left child of Item at index i is located at 2i

- right child of Item at index i is located at 2i+1

- parent of Item at index i is located at i/2

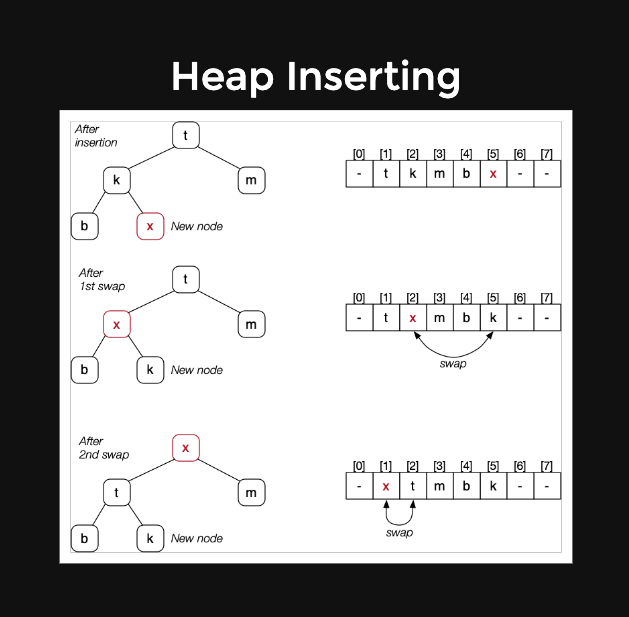
Heap Inserting:

Insertion is a two-step process

- Add new element at next available position on bottom row (but this might violate heap property; new value larger than parent)

- Reorganise vales along path to root to restore heap property

Complexity: O(log(n))

HeapInsert(Heap h, Item it):

// is there space in the array?

assert(h->nitems < h->nslots)

h->nitems++

// add new item at end of array

h->items[h->nitems] = it

// move new item to its correct place

fixUp(h->items, h->nitems)

// force value at a[i] into correct position

void fixUp(Item a[], int i)

while (i > 1 && less(a[i/2], a[i])):

swap(a, i, i/2)

i = i / 2; // integer division

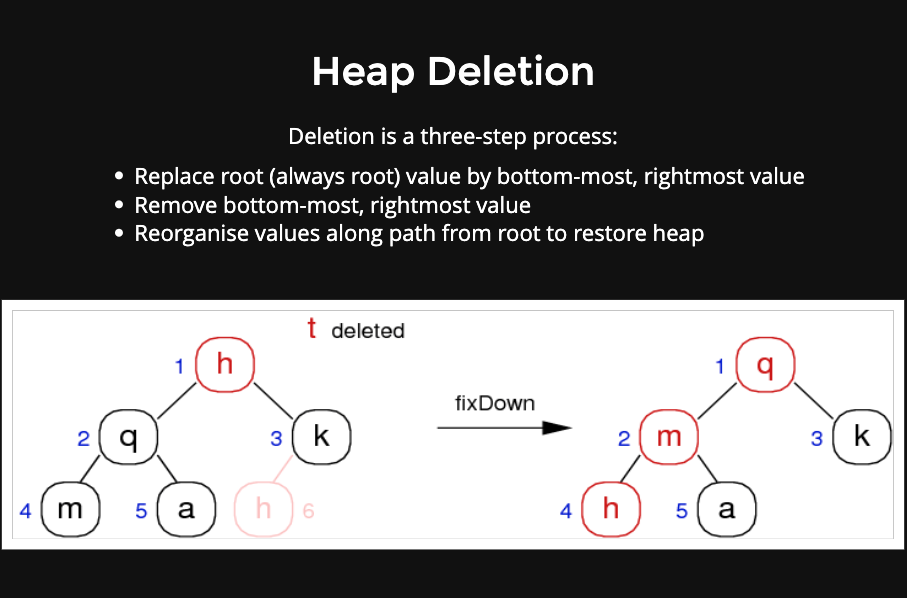
Heap Deleting:

Deletion is a three-step process:

- Replace root (always root) value by bottom-most, rightmost value

- Remove bottom-most, rightmost value

- Reorganise values along path from root to restore heap

Complexity: O(log(n))

• step 1: build heap in array
  • iterates n times, each time inserting item + ‘drifting up’ to correct place
  • overall O(n * logn)
• step 2: use heap to build sorted array
  • iterates n times, each time removing an item + adding it to different array
  • overall O(n * logn)
• overall cost = O(n * logn)

(12)

• array method:
  • normal queue ADT but instead of regular dequeue implementation, write findAndRemove function
  • findAndRemove should get item with highest priority + delete/return it + shuffle up the rest of the elements
• binary tree method (best!):
  • (not a BST because we’re not respecting the rules of node order that allow easy searching)
    • each node must be a lower/equal priority than its parent + a higher/equal priority with each of its children
    • NOT left-to-right rules from BST, just a binary tree because each node has at most two children
  • still insert nodes at root when enqueuing, but then bubble them up (through rotations) in order of priority
  • ends up so that the root is highest priority + it goes down from there in order of priority (or in vertex/value order when same priority)
  • SO can just dequeue from root
• combination method:
  • binary tree but in an array

• keep track of no. of elements being used in the array, so adding to the queue is easy (can just add to end of array rather than searching through the tree)
• to find parent, divide by 2 + round down
• when inserting a node, can check whether it should be swapped with its parent (equivalent of bubbling it up the tree)

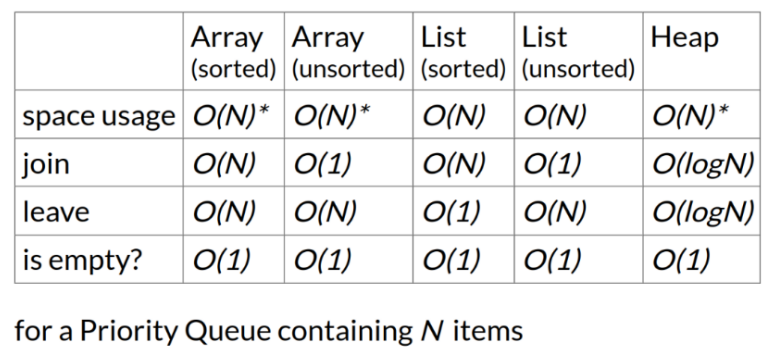
time complexity comparison

(12)

• Heaps are basically arrays that can be modeled as dense trees
  • Dense trees = no. of edges are close to maximum no. of edges possible in level order (each level has close to maximum nodes possible)
• Properties:
  • Root element is the largest element, and subsequent elements are smaller
  • For each level, the parent node is larger than both children.
  • Often implemented using arrays where index 0 is empty, and elements begin at index 1
    • Left child of item at index i is located at 2 i
    • Right child of item at index i is located at 2 i +1
    • Parent of item at index i is located at floor(i /2)

• Insertion
  • Add new element at next available position
  • Reorganise elements along path to root by value to restore heap order
• Deletion
  • Replace root element by bottom right element
  • Remove bottom right element
  • Reorganise elements along path from root to restore heap order
• Complexity:
  • For insertion:
    • Add new item at end of array ⇒ O(1)
    • Move item up into correct position ⇒ O(log2n)
    • Summary: O(log(n))
  • For deletion:
    • Replace root by item at end of array ⇒ O(1)
    • Move new root down into correct position ⇒ O(log2n)
    • Summary: O(log(n))