Graph Traversal

 

BFS process过程

DFS process过程


graph traversal pseudo essa

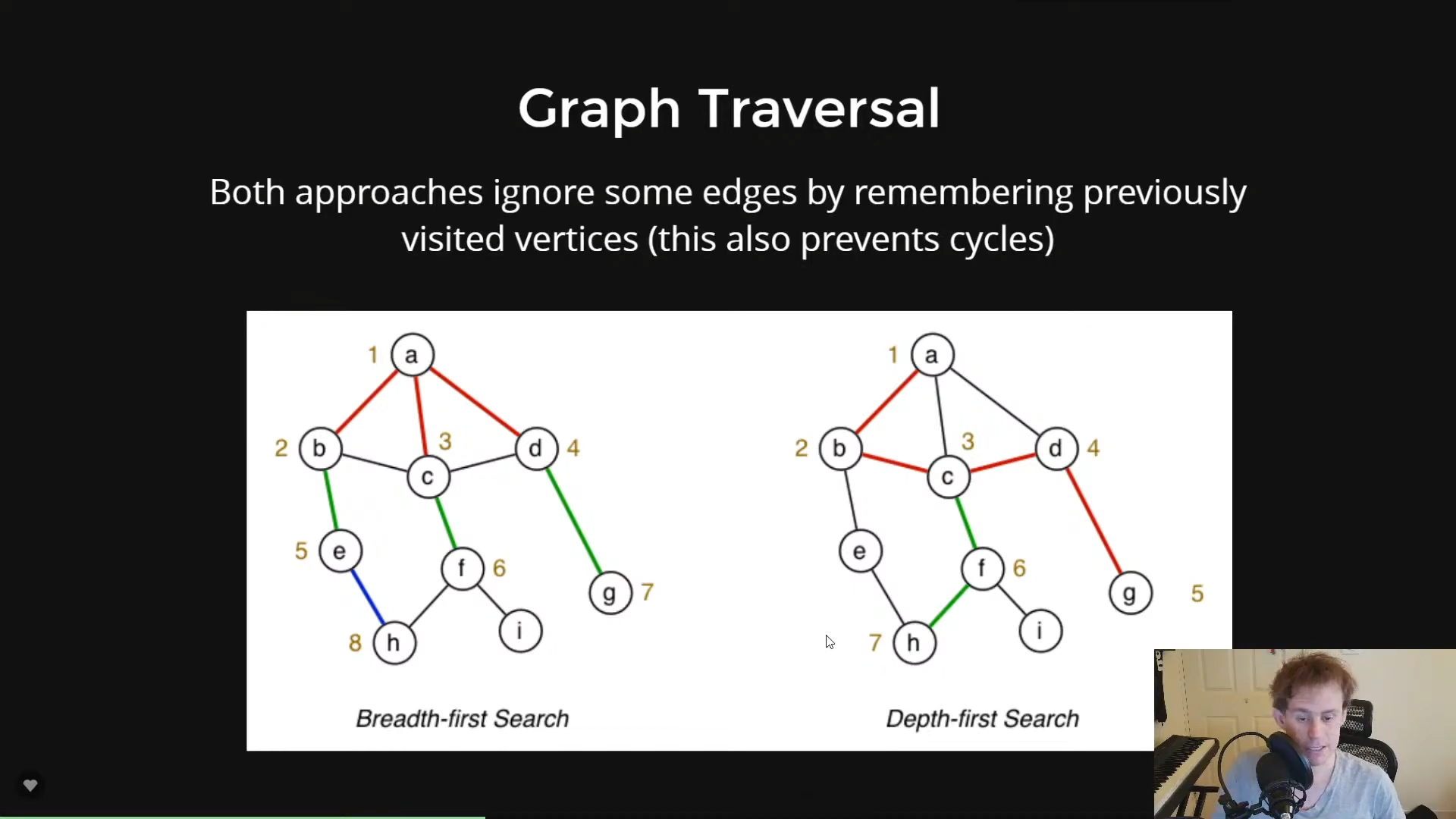
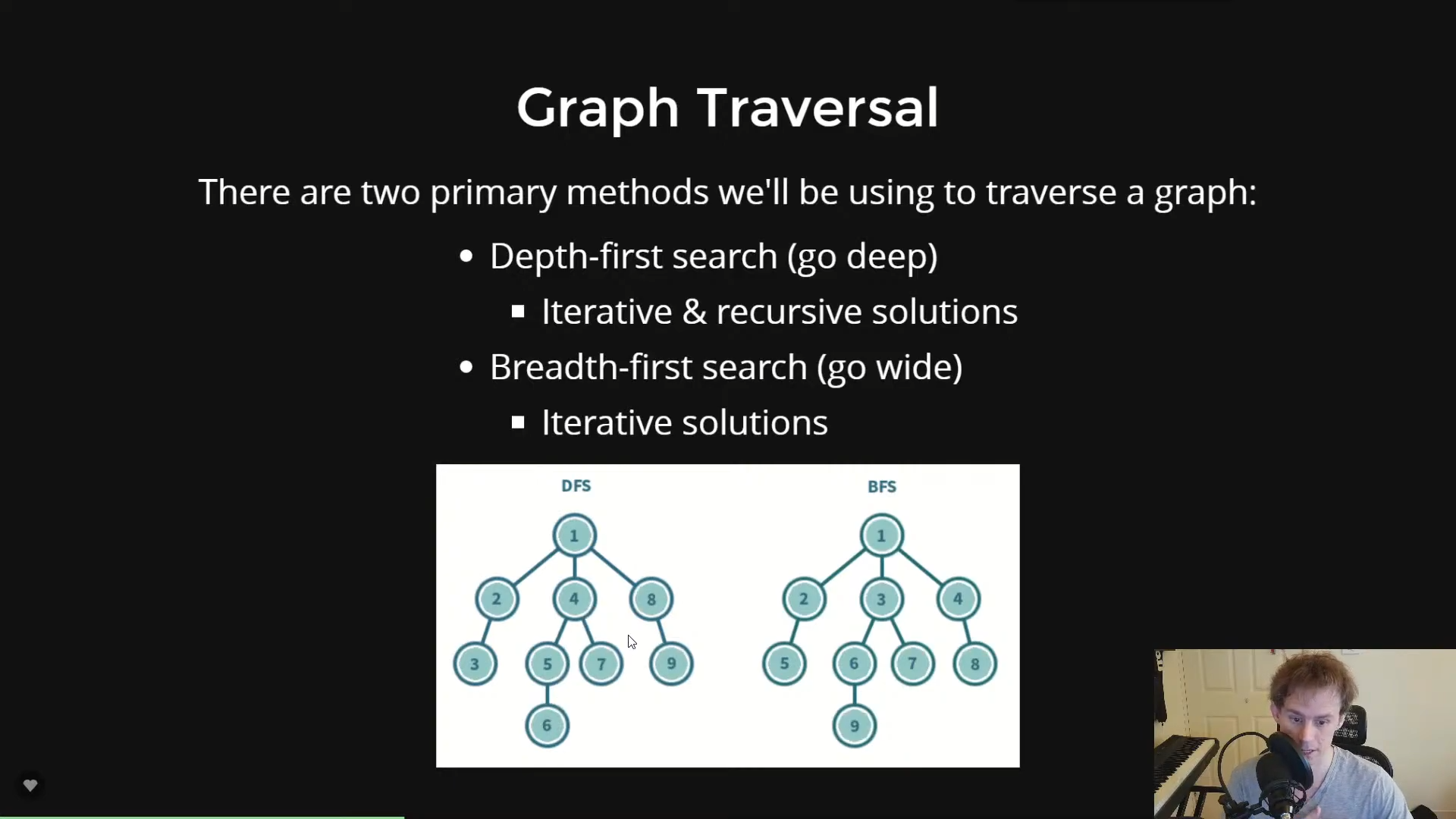
breadthfirst (takes in graph and source)

make a bool visited array, calloc it to the num verticies in graph

make a predecessor array, caclloc it to num vertices (int)

Make a new queue.

set visited of the source to true

Enqueue source,
while queue isnt empty
int v = dequeue
print v

now in a for loop iterating until num vertices: loop counter w:
if graph edges[v][w] && !visited[w]
then make visited of w true
make the pred of w = v

enqueue q,w

out of all loops
free visited, pred, queue.

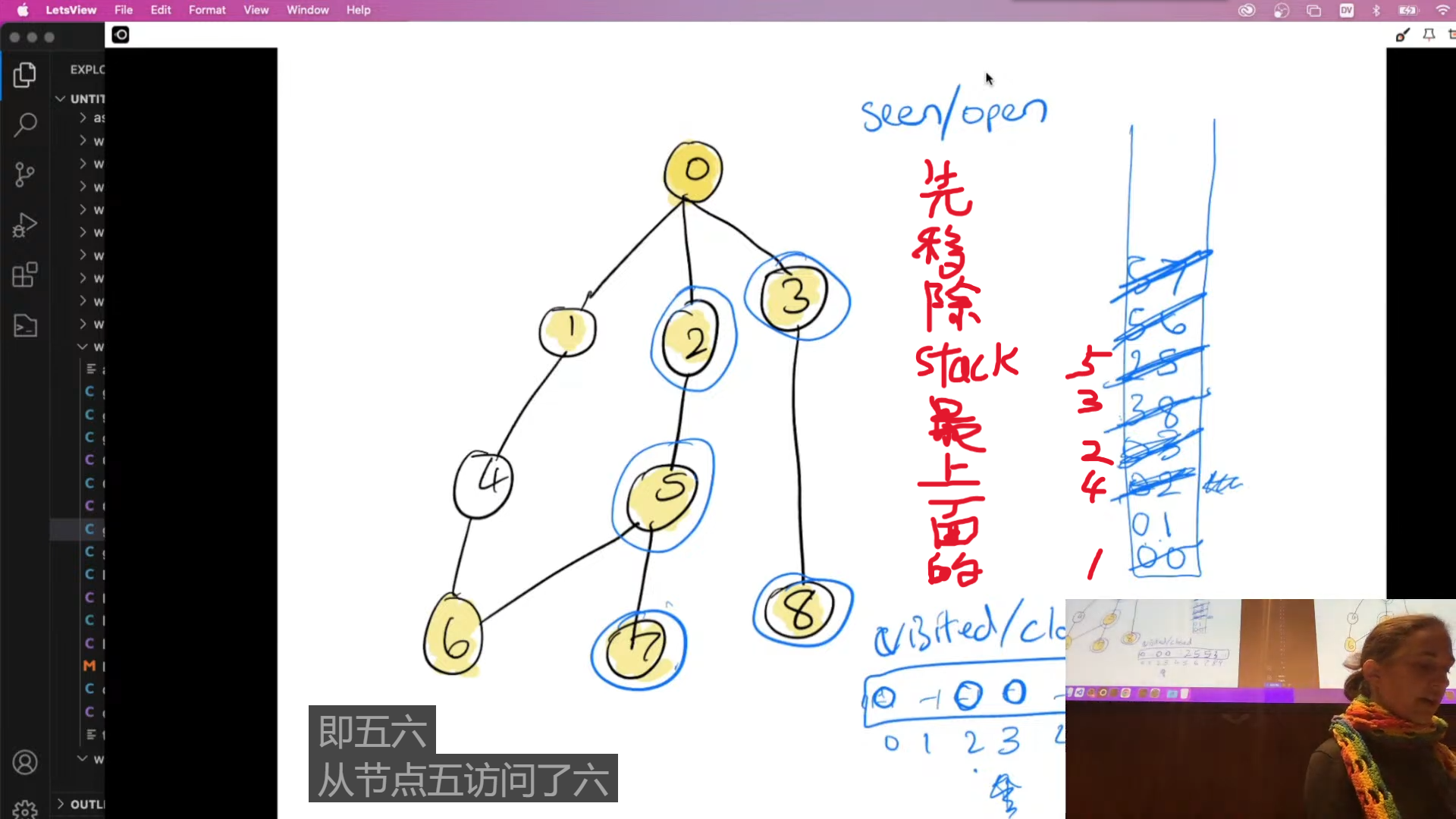
DEPTHFIRST: takes in graph, int source

difference is this uses a stack.

calloc a bool visited array to num verticies

same with int predecessor

create a stack

push stack of source

While stack isnt empty:
int v = stackpop(s)

if visited[v] continue:

set the visited of v to true
print v and a newline
in a for loop for loop counter w set to numvertices - 1, up until w>=0 w--

if graphedges[v][w] and !visited[w] then:
set the predecessor of w = w
stackpush w

out of all the loops,
free visited, predecessor and stack.





















Recursive DFS 8123

void dfs(int v, Map map, int visited[], int route[], int *route_size) {

//set current vertex as visited and add it to path

visited[v] = 1;

route[(*route_size)++] = v;

struct road roads[MapNumCities(map)];

int numRoads = MapGetRoadsFrom(map, v, roads);

//go through neighbours

for (int i = 0; i < numRoads; i++) {

if (!visited[roads[i].to]) {

dfs(roads[i].to, map, visited, route, route_size);

route[(*route_size)++] = v;

}

}

}

various type of BST pseudocode

function findPathBfs(Graph g, Vertex src, Vertex dest, int max):

pred is new int array of size g.nV

for v from 0 to g.nV - 1:

pred[v] set to -1

pred[src] set to src

make new Queue q

Enqueue src into q

bool found = false

while found is false and not QueueIsEmpty(q)

vertex v := deque from q

for vertex w from 0 to num of vertex in graph- 1

if g.edges[v][w] <= max and pred[w] == -1

pred[w] := v

if w is same with dest

found = true

break

enqueue w to queue q

free the queue q

return pred


function findPathFromSource(Graph g, Vertex src, Vertex dest, int max, int[] path):

pred get from findPathBfs(g, src, dest, max)

if pred[dest] is 1

free predecessor

return 0

set pathLength = 0

vertex curr = dest

while current is not src

path[pathLength++] := curr

curr := pred[curr]

path[pathLength++] := src


for loop with i = 0 and i < j , j = pathlength -1, i++, j--

vertex tmp := path[i]

path[i] := path[pathLength - i - 1]

path[pathLength - i - 1] := tmp

free predecessor

return pathLength


function findPathFromDest(Graph g, Vertex src, Vertex dest, int max, int[] path):

pred get from findPathBfs(g, dest, src, max)

if pred[src] == -1:

free predecessor

return 0

pathLength := 0

vertex curr := src

while curr is not dest:

path[pathLength++] := curr

curr := pred[curr]

path[pathLength++] := dest

free predecessor

return pathLength

Practice Question: Find the number of cities that are reachable 

static int doNumReachable(Graph g, int v, int visited[])
{
    visited[v] = true;
    int numR = 1;
    for (int w = 0; w < GraphNumVertices(g); w++)
    {
        if (GraphIsAdjacent(Graph g, Vertex v, Vertex w) && visited[w] == false)
        {
            numR = numR + doNumReachable(g, w, visited);
        }
    }
    return numR;
}
int numReachable(Graph g, int src) {
    bool *visited = malloc(GraphNumVertices(g) * sizeof(bool *));
    int numR = doNumReachable(g, v, visited);
    free(visited);
    return numR;
}

Practice Question: Find the furthest reachable cities 

int furthestReachable(Graph g, int src) {
    int *dist = getDistances(g, src);
    int furthest = src;
    for (int v = 0; v < GraphNumVertices(g); v++) {
        if (dist[v] != -1 && dist[v] >= dist[furthest]) {
            furthest = v;
        }
    }
    return furthest;
}
// gets the distances of all vertices from src
static int *getDistances(Graph g, int src) {
    int *pred = bfs(g, src);
    int numV = GraphNumVertices(g);
    int *distance = malloc(numV * sizeof(int *));
    for (int v = 0; v < GraphNumVertices(g); v++)
    {
        if (pred[v] == -1)
        {
            distance[v] = -1;
        }
        else
        {
            int dist = 0;
            int current = v;
            while (current != src)
            {
                dist++;
                current = pred[current];
            }
            distance[v] = dist; 
        }
    }
    free(pred);
    return distance;
}
// performs a bfs starting at src and returns an array of predecessors
static int *bfs(Graph g, int src) {
    int nV = GraphNumVertices(g);
    int *pred = malloc(nV * sizeof(int));
    for (int i = 0; i < nV; i++) {
        pred[i] = -1;
    }
    pred[src] = src;
    Queue q = QueueNew();
    QueueEnqueue(q, src);
    while (!QueueIsEmpty(q)) {
        int curr = QueueDequeue(q);
        for (int next = 0; next < nV; next++) {
            if (GraphIsAdjacent(g, curr, next) && pred[next] == -1) {
                pred[next] = curr;
                QueueEnqueue(q, next);
            }
        }
    }
    QueueFree(q);
    return pred;
}

Practice Question: Check if the graph has an Cycle

bool doHasCycle(Graph g, int v, int prev, bool visited[])
{
    visited[v] = true;
    for (int w = 0; w < GraphNumVertices(Graph g); w++)
    {
        if (GraphIsAdjacent(g, v, w))
        {
            if (visited[w] == true)
            {
                if (w != prev)
                {
                    return true;
                }
            }
            else
            {
                if (doHasCycle(g, w, v, visited))
                {
                    return true;
                }
            }
        }
    }
    return false;
}
bool hasCycle(Graph g) 
{   
    int numV = GraphNumVertices(Graph g)
    bool *visited = malloc(numV * sizeof(bool *));
    for (int v = 0; v < numV; v++)
    {
        if (visited[v] == false)
        {
            if (doHasCycle(g, v, v, visited))
            {   
                free(visited);
                return true;
            }
        }
    }
    return false;
}

num within

#include <stdio.h>

#include <stdlib.h>

#include "Graph.h"

#include "Queue.h"

static int *getDistances(Graph g, int src);

static int *bfs(Graph g, int src);


int numWithin(Graph g, int src, int dist) {

int *distances = getDistances(g, src);

int count = 0;

for (int v = 0; v < GraphNumVertices(g); v++) {

if (distances[v] >= 0 && distances[v] <= dist) {

count++;

}

}

free(distances);

return count;

}

// gets the distances of all vertices from src

static int *getDistances(Graph g, int src) {

int *pred = bfs(g, src);

int nV = GraphNumVertices(g);

int *distances = malloc(nV * sizeof(int));

for (int v = 0; v < nV; v++) {

if (pred[v] == -1) {

distances[v] = -1;

} else {

int distance = 0;

int curr = v;

while (curr != src) {

distance++;

curr = pred[curr];

}

distances[v] = distance;

}

}

free(pred);

return distances;

}

// performs a bfs starting at src and returns an array of predecessors

static int *bfs(Graph g, int src) {

int nV = GraphNumVertices(g);

int *pred = malloc(nV * sizeof(int));

for (int i = 0; i < nV; i++) {

pred[i] = -1;

}

pred[src] = src;

Queue q = QueueNew();

QueueEnqueue(q, src);

while (!QueueIsEmpty(q)) {

int curr = QueueDequeue(q);

for (int next = 0; next < nV; next++) {

if (GraphIsAdjacent(g, curr, next) && pred[next] == -1) {

pred[next] = curr;

QueueEnqueue(q, next);

}

}

}

QueueFree(q);

return pred;

}

DFS&BFS example code

void depthFirst(Graph g, int src) {

bool *visited = calloc(g->nV, sizeof(bool));

int *pred = calloc(g->nV, sizeof(int));

Stack s = StackNew();


StackPush(s, src);

while (!StackIsEmpty(s)) {

int v = StackPop(s);


if (visited[v]) continue;

visited[v] = true;


printf("%d\n", v);

for (int w = g->nV - 1; w >= 0; w--) {

if (g->edges[v][w] && !visited[w]) {

pred[w] = v;

StackPush(s, w);

}

}

}


free(visited);

free(pred);

StackFree(s);

}


void breadthFirst(Graph g, int src) {

bool *visited = calloc(g->nV, sizeof(bool));

int *pred = calloc(g->nV, sizeof(int));

Queue q = QueueNew();


visited[src] = true;

QueueEnqueue(q, src);

while (!QueueIsEmpty(q)) {

int v = QueueDequeue(q);


printf("%d\n", v);

for (int w = 0; w < g->nV; w++) {

if (g->edges[v][w] && !visited[w]) {

visited[w] = true;

pred[w] = v;

QueueEnqueue(q, w);

}

}

}


free(visited);

free(pred);

QueueFree(q);

}

BFS from any, source, destination

static int *findPathBfs(Graph g, Vertex src, Vertex dest, int max) {

int *pred = calloc(g->nV, sizeof(int));

assert(pred != NULL);

for (Vertex v = 0; v < g->nV; v++) {

pred[v] = -1;

}

pred[src] = src;

Queue q = QueueNew();

QueueEnqueue(q, src);

bool found = false;

while (!found && !QueueIsEmpty(q)) {

Vertex v = QueueDequeue(q);

for (Vertex w = 0; w < g->nV; w++) {

if (g->edges[v][w] <= max && pred[w] == -1) {

pred[w] = v;

if (w == dest) {

found = true;

break;

}

QueueEnqueue(q, w);

}

}

}

QueueFree(q);

return pred;

}


// find bfs from source

int findPath(Graph g, Vertex src, Vertex dest, int max, int *path) {

assert(g != NULL);

int *pred = findPathBfs(g, src, dest, max);

if (pred[dest] == -1) {

free(pred);

return 0;

}

// fill path array in reverse

int pathLength = 0;

Vertex curr = dest;

while (curr != src) {

path[pathLength++] = curr;

curr = pred[curr];

}

path[pathLength++] = src;

// reverse path array

for (int i = 0, j = pathLength - 1; i < j; i++, j--) {

Vertex tmp = path[i];

path[i] = path[j];

path[j] = tmp;

}

free(pred);

return pathLength;

}


// bst from destination

int findPath(Graph g, Vertex src, Vertex dest, int max, int *path) {

assert(g != NULL);

int *pred = findPathBfs(g, dest, src, max);

if (pred[src] == -1) {

free(pred);

return 0;

}

int pathLength = 0;

Vertex curr = src;

while (curr != dest) {

path[pathLength++] = curr;

curr = pred[curr];

}

path[pathLength++] = dest;

free(pred);

return pathLength;

}

check possible path

#include <assert.h>

#include <stdbool.h>

#include <stdio.h>

#include <stdlib.h>

#include "Graph.h"

int dayTrip(Graph g, Vertex s, Vertex vs[]) {

// TODO

// use the vs array as a visited array first

// check standard roads

for (int i = 0; i < g->nV; i++) {

if (g->stdEdges[s][i]) {

vs[i] = 1;

}

}

// check fast roads

for (int i = 0; i < g->nV; i++) {

if (g->fastEdges[s][i]) {

vs[i] = 1;

for (int j = 0; j < g->nV; j++) {

if (g->fastEdges[i][j] && j != s) {

vs[j] = 1;

}

}

}

}

// now convert the visited array to an array of vertices

int numReachable = 0;

for (int i = 0; i < g->nV; i++) {

if (vs[i] == 1) {

vs[numReachable++] = i;

}

}

return numReachable;

}

DFS & BFS time complexity and implementation using adjlist, adjmatrix

V (vertex), E (edges)

DFS - examines every edge and vertex

  • adj list = O(V+E)
  • adj matrix = O(V^2)

BFS - not working recursively, check visited (otherwise possibility of infinite loop)

  • adj list = O(V+E)
  • adj matrix = O(V^2)


Function that finds the furthest reachable vertex, from a source vertex

int furthestReachable(Graph g, int src) {
    int *dist = getDistances(g, src);
    int furthest = src;
    for (int v = 0; v < GraphNumVertices(g); v++) {
        if (dist[v] != -1 && dist[v] >= dist[furthest]) {
            furthest = v;
        }
    }
    return furthest;
}

// gets the distances of all vertices from src
static int *getDistances(Graph g, int src) {
    int *pred = bfs(g, src);
    int nV = GraphNumVertices(g);
    int *distances = malloc(nV * sizeof(int));
    for (int v = 0; v < nV; v++) {
        if (pred[v] == -1) {
            distances[v] = -1;
        } else {
            int distance = 0;
            int curr = v;
            while (curr != src) {
                distance++;
                curr = pred[curr];
            }
            distances[v] = distance;
        }
    }
    free(pred);
    return distances;
}

// performs a bfs starting at src and returns an array of predecessors
static int *bfs(Graph g, int src) {
    int nV = GraphNumVertices(g);
    int *pred = malloc(nV * sizeof(int));
    for (int i = 0; i < nV; i++) {
        pred[i] = -1;
    }
    pred[src] = src;
    Queue q = QueueNew();
    QueueEnqueue(q, src);
    while (!QueueIsEmpty(q)) {
        int curr = QueueDequeue(q);
        for (int next = 0; next < nV; next++) {
            if (GraphIsAdjacent(g, curr, next) && pred[next] == -1) {
                pred[next] = curr;
                QueueEnqueue(q, next);
            }
        }
    }
    QueueFree(q);
    return pred;
}

Breadth-First Search

// This is the pseudocode for breadth-first search
 bfs(g, src):
    Inputs: graph g
            starting vertex src
    create visited and predecessor arrays
    create queue and enqueue src
    mark src as visited
    while the queue is not empty:
        dequeue v
        for all edges (v, w) where w has not been visited:
            mark w as visited
            set predecessor of w to v
            enqueue w

void breadthFirstSearch(Graph g, int src) {
    int *visited = calloc(GraphNumVertices(g), sizeof(int));
     visited[src] = 1;
     Queue q = QueueNew();
     QueueEnqueue(q, src);
     while(!QueueIsEmpty(q)) {
         int v = QueueDequeue(q);
         printf("%d ", v);
         for (int w = 0; w < GraphNumVertices(g); w++) {
             if (GraphIsAdjacent(g, v, w) && !visited[w]) {
                 QueueEnqueue(q, w);
                 visited[w] = 1;
             }
         }
     }
 QueueFree(q);
 free(visited);
}

Depth-First Search

// This is the pseudocode for depth-first search
 dfs(g, src):
    Inputs: graph g
            starting vertex src
    create visited and predecessor arrays
    create stack and push src
    while the stack is not empty:
        pop v
        if v has been visited:
            continue (i.e., return to beginning of loop)
        mark v as visited
        for all edges (v, w) where w has not been visited:
            set predecessor of w to v
            push w

void depthFirst ( Graph g , int src ) {

bool * visited = calloc ( g -> nV , sizeof ( bool ));

int * pred = calloc ( g -> nV , sizeof ( int ));

Stack s = StackNew (); StackPush ( s , src );

while ( ! StackIsEmpty ( s )) {

int v = StackPop ( s );

if ( visited [ v ]) continue ;

visited [ v ] = true ; printf ( "%d \n " , v );

for ( int w = g -> nV - 1 ; w >= 0 ; w -- ) {

if ( g -> edges [ v ][ w ] && ! visited [ w ]) {

pred [ w ] = v ; StackPush ( s , w );

}

}

}

free ( visited );

free ( pred );

StackFree ( s );

} 

static void dfsRecursive(Graph g, int v, int *visited) {
    printf("%d ", v);
    visited[v] = 1;
    for (int w = 0; w < GraphNumVertices(g); w++) {
        if (GraphIsAdjacent(g, v, w) && !visited[w]) {
            dfsRecursive(g, w, visited);
        }
    }
}

void depthFirstSearch(Graph g, int src) {
    int *visited = calloc(GraphNumVertices(g), sizeof(int));
    dfsRecursive(g, src, visited);
    free(visited);
}