Graph Implementation

There are essentially three graph implementations, listed below

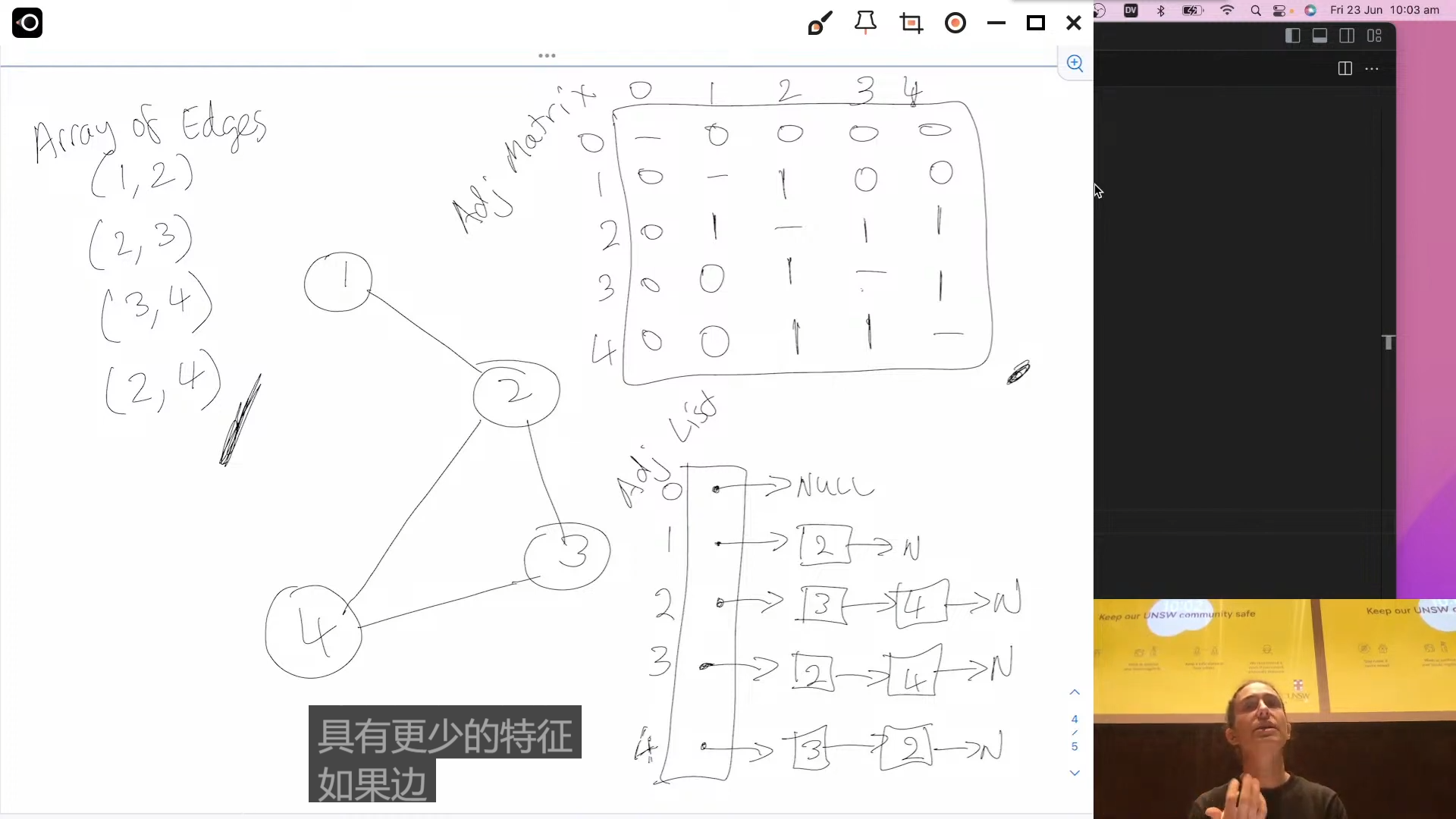
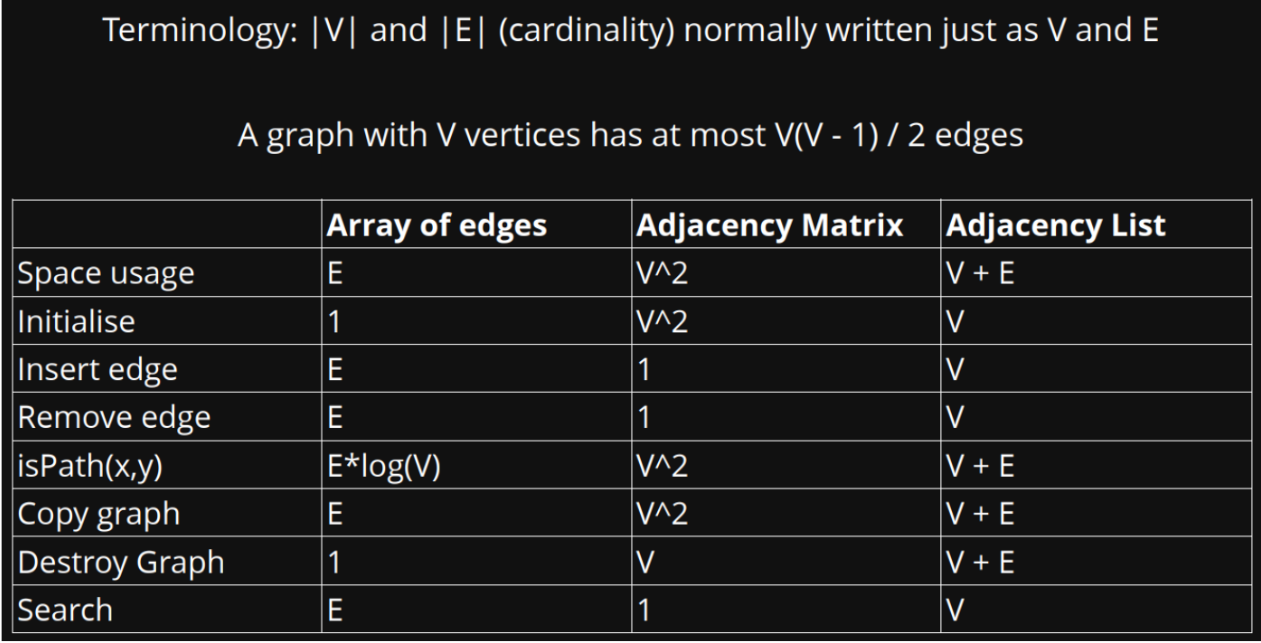
1. Adjacency Matrix: An adjacency matrix is a two-dimensional array where each cell (i, j) represents whether there is an edge between node i and node j. If the graph is weighted, the cell can store the weight of the edge. The value in the cell can be a boolean (for unweighted graphs) or a number (for weighted graphs).

Advantages:

• Constant-time O(1) access to check if an edge exists between two nodes.
• Efficient for dense graphs (graphs with many edges).
• Suitable for graphs with a fixed number of nodes.

Disadvantages:

• Consumes more space for sparse graphs (graphs with few edges).
• Adding or removing nodes requires resizing the matrix, which can be costly.

1. Adjacency List: An adjacency list is a data structure where each node is associated with a list (or array) of its neighboring nodes. For a weighted graph, each element in the list can store the weight of the edge.

Advantages:

• Memory-efficient for sparse graphs.
• Efficient for graph algorithms that involve traversing neighbors.
• Adding or removing nodes/edges is more efficient than with an adjacency matrix.

Disadvantages:

• Slower edge existence check (requires traversing the adjacency list).
• May consume more memory for dense graphs.

1. Array of Edges (Edge List): An array of edges represents the graph as an array where each element represents an edge. Each edge is defined by its two endpoints (nodes) and possibly a weight.

Advantages:

• Minimal memory overhead.
• Simple structure, suitable for basic graph representations.
• Good for storing just the essential information about the graph.

Disadvantages:

• Edge existence check can be inefficient if the array is not sorted or indexed.
• Traversing neighbors may require additional data structures.

helper

Edges:

Matrix:

List:

1

Overall Comparison of all 3

newGraph(V):
 g.nV = V // #vertices (numbered 0..V-1)
 g.nE = 0 // #edges
 allocate memory for g.edges[]
 for all i=0..V-1:
     g.edges[i]=newList() // empty list
 return g

insertEdge(g,(v,w)):
 if not ListMember(g.edges[v],w):
     // (v,w) not in graph
     ListInsert(g.edges[v],w)
     ListInsert(g.edges[w],v)
     g.nE=g.nE+1

removeEdge(g,(v,w)):
 if ListMember(g.edges[v],w):
     // (v,w) in graph
     ListDelete(g.edges[v],w)
     ListDelete(g.edges[w],v)
     g.nE=g.nE-1

showEdges(g):
 for all i=0 to g.nV-1:
     for all v in g.edges[i]:
         if i < v:
             print i"—"v

newGraph(V):
 g.nV = V // #vertices (numbered 0..V-1)
 g.nE = 0 // #edges
 allocate memory for g.edges[][]
 for all i,j=0..V-1:
     g.edges[i][j] = 0 // false
 return g

insertEdge(g,(v,w)):
 if g.edges[v][w] = 0: // (v,w) not in graph
     g.edges[v][w]=1 // set to true
     g.edges[w][v]=1
     g.nE=g.nE+1


removeEdge(g,(v,w)):
 if g.edges[v][w] ≠ 0: // (v,w) in graph
     g.edges[v][w]=0 // set to false
     g.edges[w][v]=0
     g.nE=g.nE - 1


showEdges(g): 
for all i=0 to g.nV-1: 
    for all j=i+1 to g.nV-1: 
        if g.edges[i][j] ≠ 0 then 
            print i"—"j

newGraph(V):
 g = new Graph with V verticies
 g.nV = V // #vertices (numbered 0..V-1)
 g.nE = 0 // #edges
 allocate enough memory for g.edges[]
 return g

insertEdge(g,(v,w)):
i=0
while i < g.nE and g.edges[i] ≠ (v,w):
    i = i + 1
    if i = g.nE: // (v,w) not found
    g.edges[i] = (v,w)
    g.nE = g.nE + 1 

removeEdge(g,(v,w)):
i = 0 
while i < g.nE and g.edges[i] ≠ (v,w):
    i = i + 1
    if i < g.nE: // (v,w) found
    g.edges[i] = g.edges[g.nE-1]
    g.nE = g.nE - 1

showEdges(g): 
for all i=0 to g.nE-1:
    (v,w) = g.edges[i]
    print v"—"w


Array of Edges Cost:

DFS (Graph g, int src) {

int visited;

dfs(g, src, visited);

free(visited);

}

dfs(g,v,visited) {

visited[v] = 1;

for (all w) {

if (Adjacent(g, v, w) && !visited[w]) {

dfs(g, w, visited);

}

}

}

#include <stdbool.h>

#include <stdio.h>

#include <stdlib.h>

#include "Graph.h"

// Declare any helper functions you need here.

bool stackHasNode(int stack[], int stackSize, int node);

/**

* Determines whether the given graph has a cycle.

*

* Input:

* - Graph g: An unweighted, undirected, connected graph

* represented using an adjacency matrix. Has at least one vertex.

* Output:

* - bool: true if the graph has a cycle, false otherwise.

*/

bool graphDetectCycle(Graph g) {

bool hasCycle = false;

// declare visited array

bool visited[MAX_NUM_VERTICES] = {};

// declare stack and initialise with first node

int toVisitStack[4*MAX_NUM_VERTICES] = {};

toVisitStack[0] = 0;

int stackTop = 1;

while (!hasCycle && stackTop > 0) {

int node = toVisitStack[--stackTop];

if (!visited[node]) {

visited[node] = true;

for (int otherNode = 0; otherNode < numVertices(g); otherNode++) {

if (otherNode == node || !adjacent(g, node, otherNode)) {

continue;

}

// printf("Checking %d's neighbour %d\n", node, otherNode);

if (!visited[otherNode]) {

if (stackHasNode(toVisitStack, stackTop, otherNode)) {

// If we plan to visit a node that we already planned

// to visit from a different node, we have a cycle.

hasCycle = true;

break;

} else {

// Neighbour has not been visited yet and there is

// presently no plan to visit it - make a plan

// to visit it.

toVisitStack[stackTop++] = otherNode;

}

}

}

}

}

return hasCycle;

}

bool stackHasNode(int stack[], int stackSize, int node) {

for (int i = 0; i < stackSize; i++) {

if (stack[i] == node) {

return true;

}

}

return false;

}

• array of edges → list of (v,w) vertex pairs
  • used if graph has very few edges (other representations would be waste of space)
  • if lots of edges, array is harder to search through to find which vertices are connected
  • gets much longer for directed matrix with some bidirectional edges
  • to store weighted graph, add extra value to each array
• adjacency matrix → edges defined by value in V*W matrix
  • easier to search for paths in directed graph
  • can store 0 vs. 1 for undirected OR weight for directed graph
• adjacency list → array of graph values, with each value as a pointer to linked list of nodes it’s connected to
  • saves space if graph has fewer edges
  • easier to find edges than in array of edges (can jump to value, then move through list)
  • to store weighted graph, would include value in list node
• time complexity comparison:

(12)

The minimum possible number of edges would occur when the vertices are connected in a single line, which is 6 - 1 = 5 edges.

The maximum possible number of edges would occur when the graph is complete, which is (5 x 6)/2 = 15 edges.

typedef struct graph {
    int nV;         // #vertices
    int nE;         // #edges
    double **edges; // adjacency matrix storing positive weights
                    // 0 if nodes not adjacent
} *Graph;
Graph GraphNew(int nV) {
    assert(nV > 0);
    Graph g = malloc(sizeof(*g));
    if (g == NULL) {
        fprintf(stderr, "error: out of memory\n");
        exit(EXIT_FAILURE);
    }
    g->nV = nV;
    g->nE = 0;
    g->edges = malloc(nV * sizeof(double *));
    if (g->edges == NULL) {
        fprintf(stderr, "error: out of memory\n");
        exit(EXIT_FAILURE);
    }
    for (int i = 0; i < nV; i++) {
        g->edges[i] = calloc(nV, sizeof(double));
        if (g->edges[i] == NULL) {
            fprintf(stderr, "error: out of memory\n");
            exit(EXIT_FAILURE);
        }
    }
    return g;
}