Hamiltonian vs Euler:
Connected components:
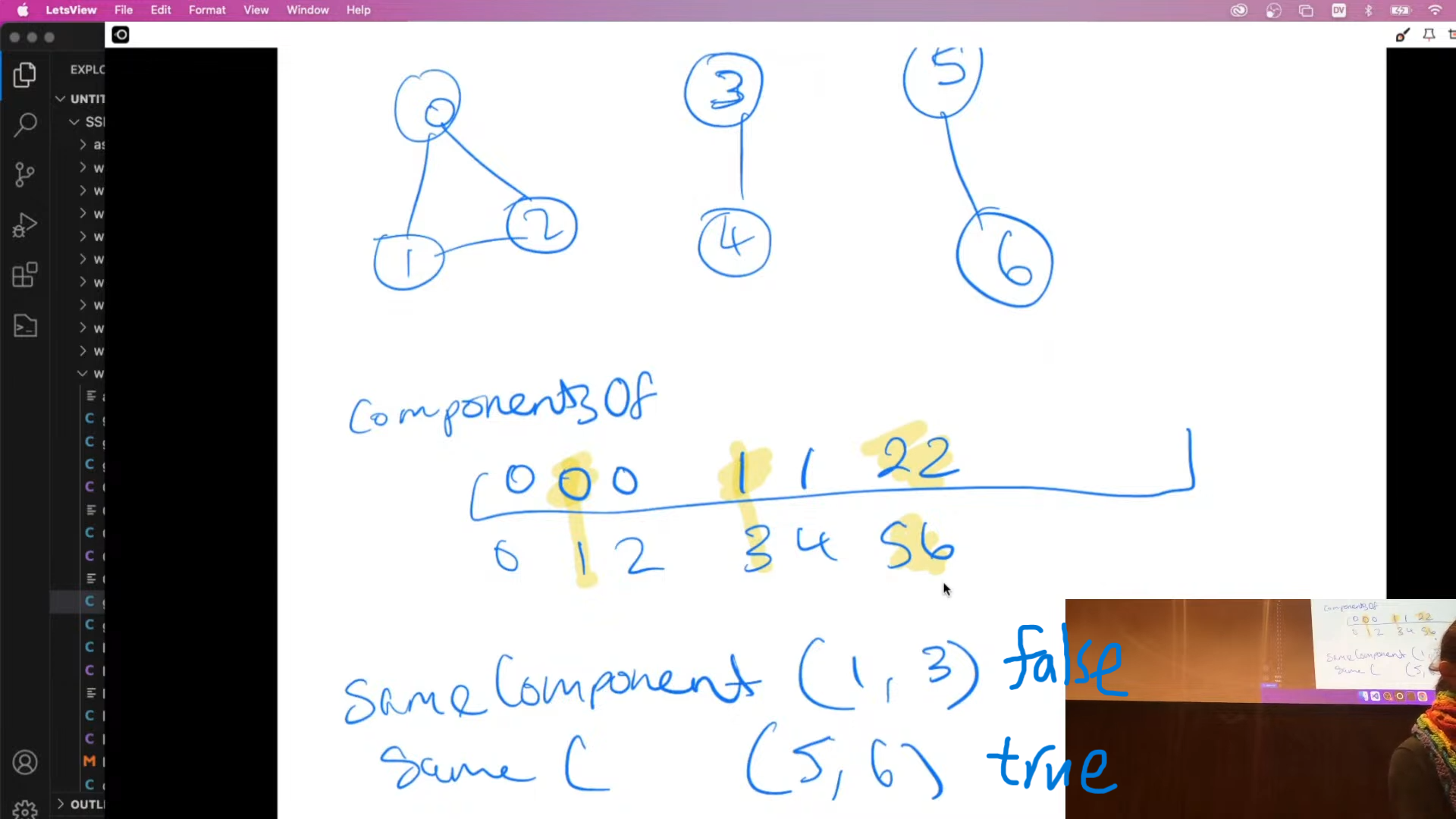
Hamiltonian vs Euler:

(12)

(12)
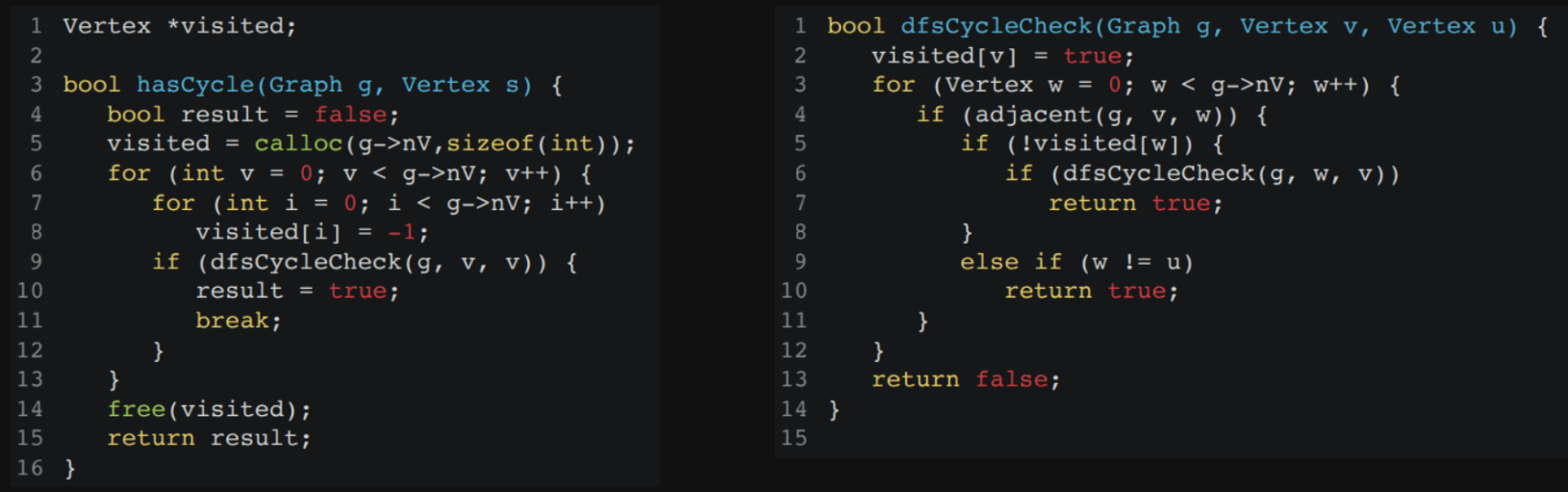
(12)
for better error checking, modify hasCycle to
if (!visited[v] && doHasCycle(g, v, v, visited)) {
result = true;
break;
}
A simple graph with n vertices (n ≥ 3) is Hamiltonian if every vertex has degree n / 2 or greater
A graph has an Euler circuit if and only if the <g-bubble> degree </g-bubble> of every vertex is even and it is connected.
A graph has a Euler circuit if and only if it is connected and ALL vertices have an even degree.
fixed. thanks for that.
// The following is the pseudocode for Kruskal's Algorithm, which find the minimum spanning tree of a graph.
KruskalMST(G):
MST=empty graph
sort edges(G) by weight
for each e ∈ sortedEdgeList:
MST = MST ∪ {e} // add edge
if MST has a cyle:
MST = MST \ {e} // drop edge
if MST has n-1 edges:
return MST
// The following is the pseudocode for Prim's algorithm, which finds the minimum spanning tree of a graph.
PrimMST(G):
MST = empty graph
usedV = {0}
unusedE = edges(g)
while |usedV| < n:
find e = (s,t,w) ∈ unusedE such that {
s ∈ usedV ∧ t ∉ usedV
(∧ w is min weight of all such edges)
}
MST = MST ∪ {e}
usedV = usedV ∪ {t}
unusedE = unusedE \ {e}
return MST
// This is the pseudocode for Dijkstra's Algorithm, which finds the shortest path from a source vertex
to all other vertices
dijkstraSSSP(G,source):
dist[] // array of cost of shortest path from s
pred[] // array of predecessor in shortest path from s
vSet // vertices whose shortest path from s is unknown
initialise all dist[] to ∞
dist[source]=0
initialise all pred[] to -1
vSet = all vertices of G
while vSet is not empty:
find v in vSet with minimum dist[v]
for each (v,w,weight) in edges(G):
relax along (v,w,weight)
vSet = vSet \ {v}
Time complexity
* Each edge needs to be considered once, which is O(E).
* The outer while loop has O(V) iterations.
* If you try to find the shortest path for every vertex...
* We have a cost of O(E) to go through each edge.
* To find the shortest path from the source to somewhere that costs O(V).
* If we try to do that for each vertex - $V$ times - then the total cost is O(E + V^2), ergo O(V^2).
* E gets simplified because E < V^2 always.
Non pseudocode version of the same logic:
-> add all paths from current node to queue, marking the current node as expanded and make note of the cumulative cost to get to each of the new destinations
-> then make the current node the shortest cost non-expanded path of all items in the queue and repeat
-> once the destination node has been expanded, the shortest path to it has been found
if dist[v] + weight(v, w) < dist[w]:
dist[w] <- dist[v] + weight(v, w)
pred[w] <- v