Connected / Complete Graph:
Graph terms
Degree of a vertex - how many edges go out from the vertex
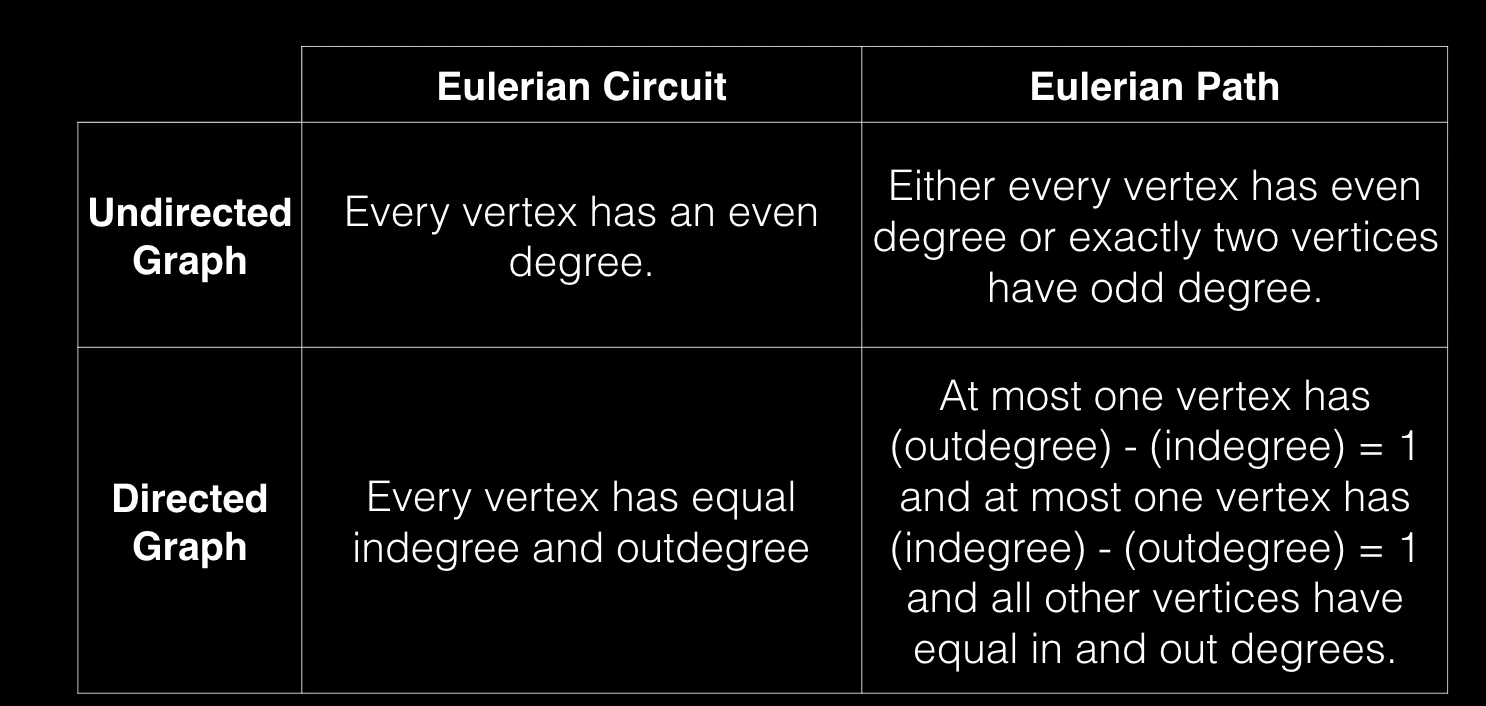
Euler path - path that visits each edge exactly once. only exists if graph has exactly 2 odd verticies
Hamiltonian path - path that visits each vertex exactly once
Euler circuit - Euler path that ends at the same vertex it started at.
If all the vertices of a graph have even degree, then the graph has an Euler circuit
Hamiltonian circuit - Hamiltonian path that has an edge connecting back to the start of the path
Subgraph - graph that is made up of verticies in a graph.
Graph component - connected subgraph that is not part of any larger connected subgraph.
On the amount of edges
- A graph with V vertices will have no more than V(V - 1)/2 edges.
- It will have no less than V-1 edges, too.
- The ratio of edges to vertices can vary considerably.
- If the amount of edges is near V^2, the graph is dense.
- If the amount of edges is nearer to V, the graph is sparse (eg linked list-esque data structures)
On the amount of connected components
- The minimum number of connected components in an undirected graph is V.
- The maximum number is E + (V - 1).
components(G):
for all vertices v in G:
componentOf[v] = -1
compID = 0
for all vertices v in G:
if componentOf[v] == -1:
dfsComponent(G, v, compID)
compID = compID + 1
dfsComponent(G, v, id):
componentOf[v] = id
for each (v, w) in g->edges:
if componentOf[w] == -1:
dfsComponent(G, w, id)
// it's wise to cache these results
typedef struct GraphRep *Graph;
struct GraphRep {
// ...
int nC; // number of connected components
int *cc; // which component each vertex is
// contained in.
// ie [0 .. nV - 1] of 0 .. nC - 1
}
Directed graphs
- The outdegree (deg(v)) of a vertex is the number of edges pointing outwards ie (v, _)
- The indegree (deg^-1(v)) is the number of edges pointing towards the vertex ie (_, v)
- Reachability concerns whether w is reachable from v if there is a directed path v, ..., w.
- A digraph has strong connectivity if every vertex is reachable from every other vertex.
- A directed acyclic graph has no cycles.
Cycle checking
-
A graph has a cycle if, at any point in the graph, it has...
- A path length of two or greater.
- The start vertex of the path is equal to the end vertex.
- We use an edge in this path no more than once.
Vertex *visited;
bool hasCycle(Graph g, Vertex s) {
bool result = false;
visited = calloc(g->nV, sizeof(int));
for (int v = 0; v < g->nV; v++) {
for (int i = 0; i < g->nV; i++) {
visited[i] = -1;
}
if (dfsCycleCheck(g, v, v)) {
result = true;
break;
}
}
free(visited);
return result;
}
bool dfsCycleCheck(Graph g, Vertex v, Vertex u) {
visited[v] = true;
for (Vertex w = 0; w < g->nV; w++) {
if (adjacent(g, v, w)) {
if (!visited[w]) {
if (dfsCycleCheck(g, w, v)) {
return true;
}
}
else if (w != u) {
return true;
}
}
}
return false;
}
Connected / Complete Graph
Euler Path and Circuit Theory
Euler Path and Circuit Theory
Graph Terminology Photo
Graph Terminology Photo
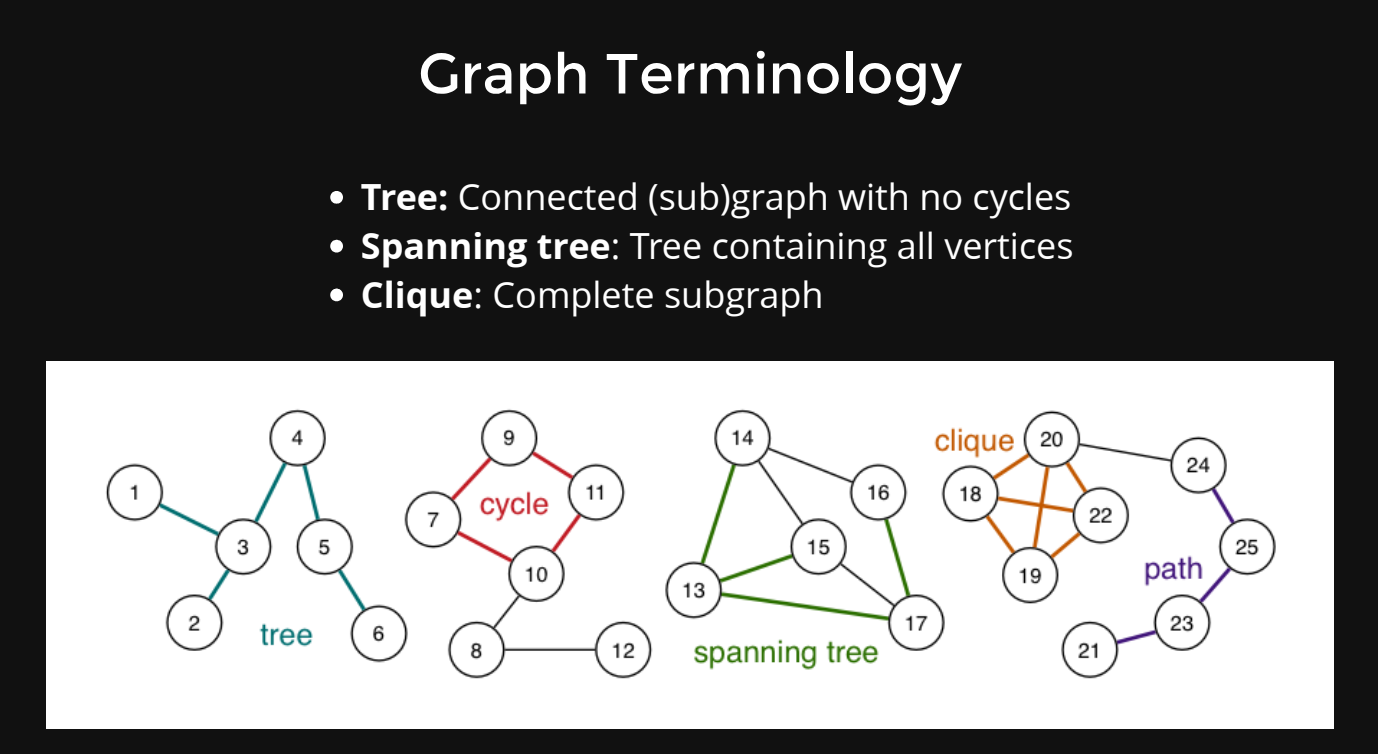
graph terminology
- vertices are adjacent if they have an edge between them
- edge is incident on a vertex if it touches that vertex
-
path
= sequence of vertices where each vertex has an edge to its predecessor
- cycle if last vertex = first vertex
- length of path = number of edges
- connected graph = path from each vertex to every other vertex (usually true)
- complete graph = edge from each vertex to every other vertex
(12)