COMP2521: Assignment 2
Social Network Analysis
A notice on the class web page will be posted after each major revision.
Please check the class notice board and this assignment page frequently (for Change Log).
The specification may change.
FAQ:
You should check Ass2 FAQ, it may offer answers to your queries!
Change log:
- 07:15pm Thursday 14/Nov: Instructions on "how to submit" your assignment are now available,
go to the
Sumission section.
Objectives
- to implement graph based data analysis functions (ADTs) to mine a given social network.
- to give you further practice with C and data structures (Graph ADT)
Admin
| Marks |
20 marks (scaled to 14 marks towards total course mark)
|
| Individual Assignment |
This assignment is an individual assignment. |
| Due |
08:00pm Friday 22 November 2019 |
Late
Penalty |
2 marks per day off the ceiling.
Last day to submit this assignment is 8pm Monday 25 November 2019, of course with late penalty.
|
| Submit |
TBA
|
Aim
In this assignment, your task is to implement graph based data analysis functions (ADTs) to mine a given social network. For example, detect say "influenciers", "followers", "communities", etc. in a given social network.
You should start by reading the Wikipedia entries on these topics. Later I will also discuss these topics in the lecture.
The main focus of this assignment is to calculate measures that could identify say "influenciers", "followers", etc., and also discover possible "communities" in a given social network.
Dos and Don'ts !
Please note that,
- For this assignmet you can use source code that is available as part of the course material (lectures, exercises, tutes and labs). However, you must properly acknowledge it in your solution.
- All the required code for each part must be in the respective *.c file.
- You may implement additional helper functions in your files, please declare them as "static" functions.
- After implementing Dijkstra.h, you can use this ADT for other tasks in the assignment. However, please note that for our testing, we will use/supply our implementation of Dijkstra.h. So your programs MUST NOT use any implementation related information that is not available in the respective header files (*.h files). In other words, you can only use information available in the corresponding *.h files.
- Your program must not have any "main" function in any of the submitted files.
- Do not submit any other files. For example, you do not need to submit your modified test files or *.h files.
- If you have not implemented any part, must still submit an empty file with the corresponding file name.
.
Provided Files
We are providing implementations of Graph.h and PQ.h .
You can use them to implement all three parts.
However, your programs MUST NOT use any implementation related information
that is not available in the respective header files (*.h files).
In other words, you can only use information available in
the corresponding *.h files.
Also note:
- all edge weights will be greater than zero.
- we will not be testing reflexive and/or self-loop edges.
- we will not be testing the case where the same edge is inserted twice.
Download files:
Part-1: Dijkstra's algorithm
In order to discover say "influencers", we need to repeatedly find shortest paths between all pairs of nodes.
In this section, you need to implement Dijkstra's algorithm to discover shortest paths from a given source to all other
nodes in the graph.
The function offers one important additional feature, the function keeps track of multiple predecessors for
a node on shortest paths from the source, if they exist.
In the following example, while discovering shortest paths from source node '0', we
discovered that there are two possible shortests paths from node '0' to node '1' (0->1
OR 0->2->1),
so node '1' has two possible predecessors (node '0' or node '2') on possible shortest paths, as shown below.
We will discuss this point in detail in a lecture. The basic idea is, the array of lists ("pred")
keeps one linked list per node, and
stores multiple predecessors (if they exist) for that node on shortest paths from a given source.
In other words, for a given source, each linked list in "pred" offers possible predecessors for the corresponding node.
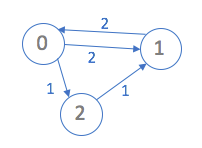
|
Node 0
Distance
0 : X
1 : 2
2 : 1
Preds
0 : NULL
1 : [0]->[2]->NULL
2 : [0]->NULL
Node 1
Distance
0 : 2
1 : X
2 : 3
Preds
0 : [1]->NULL
1 : NULL
2 : [0]->NULL
Node 2
Distance
0 : 3
1 : 1
2 : X
Preds
0 : [1]->NULL
1 : [2]->NULL
2 : NULL
|
The function returns 'ShortestPaths' structure with the required information
(i.e. 'distance' array, 'predecessor' arrays, source and no_of_nodes in the graph)
Your task:
In this section, you need to implement the following file:
- Dijkstra.c that implements all the functions defined in
Dijkstra.h.
Part-2: Centrality Measures for Social Network Analysis
Centrality measures play very important role in analysing a social network. For example, nodes with higher "betweenness" measure often correspond to "influencers" in the given social network. In this part you will implement two well known centrality measures for a given directed weighted graph.
Descriptions of some of the following items are from Wikipedia at Centrality, adapted for this assignment.
Closeness Centrality
Closeness centrality (or closeness) of a node is calculated as the sum of the length of the shortest paths between the node (\(x\)) and all other nodes (\(y \in V \land y \ne x\)) in the graph. Generally closeness is defined as below,
$$ C(x)= {1 \over \sum_{y} d(y, x) }.$$
where \( d(y,x) \) is the shortest distance between vertices \(x \) and \(y\).
However, considering most likely we will have isolated nodes, for this assignment you need to
use Wasserman and Faust formula to calculate closeness of a node in a directed graph as described below:
$$ C_{WF}(u)= { n - 1 \over N - 1 } * { n - 1 \over \sum_{all\ v\ reachable\ from\ u} d(u,v) }.$$
where \( d(u,v) \) is the shortest-path distance in a directed graph from vertex \(u\) to \(v\),
\(n\) is the number of nodes that \(u\) can reach, and \(N\) denote the number of nodes in the graph.
For further explanations, please read the following document, it may answer many of your questions!
Based on the above, the more central a node is, the closer it is to all other nodes.
For for information, see Wikipedia entry on Closeness centrality.
Betweenness Centrality
The betweenness centrality of a node \(v\) is given by the expression:
$$ g(v)=\sum _{{s\neq v\neq t}}{\frac {\sigma _{{st}}(v)}{\sigma _{{st}}}} $$
where \(\sigma_{st}\) is the total number of shortest paths from node \(s\) to node \(t\) and \(\sigma_{st}(v)\) is the number of those paths that pass through \(v\).
For this assignment, use the following approach to calculate normalised betweenness centrality. It is easier! and also avoids zero as denominator (for n>2).
$$ {\mbox{normal}}(g(v))= {\frac {1}{((n-1)(n-2))} } *{g(v)} $$
where, \(n\) represents the number of nodes in the graph.
For further explanations, please read the following document, it may answer many of your questions!
Your task:
In this section, you need to implement the following file:
For more information, see Wikipedia entry on Betweenness centrality
Part-3: Discovering Community
In this part you need to implement the Hierarchical Agglomerative Clustering (HAC) algorithm to discover communities in a given graph. In particular, you need to implement Lance-Williams algorithm, as described below. In the lecture we will discuss how this algorithm works, and what you need to do to implement it. You may find the following document/video useful for this part:
Distance measure: For this assignment, we calculate distance between a pair of vertices as follow:
Let \(wt\) represents maximum edge weight of all available weighted edges between a pair of vertices \(v\) and \(w\).
Distance \(d\) between vertices \(v\) and \(w\) is defined as \(d = 1/wt\). If \(v\) and \(w\) are not connected, \(d\) is infinite.
For example, if there is one directed link between \(v\) and \(w\) with weight \(wt\), the distance between them is \(1/wt\). If there are two links, between \(v\) and w, we take maximum of the two weights and the distance between them
is \(1/max(wt_{vw}, wt_{wv})\). Please note that, one can also consider alternative approaches, like take average, min, etc. However, we need to pick one approach for this assignment and we will use the above distance measure.
You need to use the following (adapted) Lance-Williams HAC Algorithm to derive a dendrogram:
- Calculate distances between each pair of vertices as described above.
- Create clusters for every vertex \(i\), say \(c_{i}\).
- Let \(Dist(c_{i},c_{j})\) represents the distance between cluster \(c_{i}\) and \(c_{j}\), initially it represents distance between vertex \( i \) and \( j \) .
- For k = 1 to N-1
- Find two closest clusters, say \(c_{i}\) and \(c_{j}\). If there are multiple alternatives,
you can select any one of the pairs of closest clusters.
- Remove clusters \(c_{i}\) and \(c_{j}\) from the collection of clusters and
add a new cluster \(c_{ij}\) (with all vertices in \(c_{i}\) and \(c_{j}\)) to the collection of clusters.
- Update dendrogram.
- Update distances, say \(Dist(c_{ij},c_{k})\), between the newly added cluster \(c_{ij}\) and
the rest of the clusters (\(c_{k}\)) in the collection using Lance-Williams formula using the selected method
('Single linkage' or 'Complete linkage' - see below).
- End For
- Return dendrogram
Lance-Williams formula:
$$ Dist(c_{ij},c_{k}) = \alpha_{i} * Dist(c_{i},c_{k}) + \alpha_{j} * Dist(c_{j},c_{k}) + \beta * Dist(c_{i},c_{j}) + \gamma * abs(Dist(c_{i},c_{k}) - Dist(c_{j},c_{k}) )
$$
where \(\alpha_{i}\), \(\alpha_{j}\), \(\beta\), and \(\gamma\) define the agglomerative criterion.
For the Single link method, these values are:
\(\alpha_{i} = 1/2 \), \(\alpha_{j} = 1/2 \), \(\beta = 0\), and \(\gamma = -1/2 \). Using these values, the formula for Single link method is:
$$ Dist(c_{ij},c_{k}) = 1/2 * Dist(c_{i},c_{k}) + 1/2 * Dist(c_{j},c_{k}) -1/2 * abs(Dist(c_{i},c_{k}) - Dist(c_{j},c_{k}) )
$$
We can simplify the above and re-write the formula for Single link method as below
$$ Dist(c_{ij},c_{k}) = min ( Dist(c_{i},c_{k}), Dist(c_{j},c_{k}) ) $$
For the Complete link method, the values are:
\(\alpha_{i} = 1/2 \), \(\alpha_{j} = 1/2 \), \(\beta = 0\), and \(\gamma = 1/2 \). Using these values, the formula for Complete link method is:
$$ Dist(c_{ij},c_{k}) = 1/2 * Dist(c_{i},c_{k}) + 1/2 * Dist(c_{j},c_{k}) + 1/2 * abs(Dist(c_{i},c_{k}) - Dist(c_{j},c_{k}) )
$$
We can simplify the above and re-write the formula for Complete link method as below
$$ Dist(c_{ij},c_{k}) = max ( Dist(c_{i},c_{k}), Dist(c_{j},c_{k}) ) $$
Please see the following simple example, it may answer many of your questions!
Your task:
In this section, you need to implement the following file:
Assessment Criteria
- Part-1: Dijkstra's algorithm (20% marks)
- Part-2:
- Closeness Centrality (22% marks),
- Betweenness Centrality (23% marks)
- Part-3: Discovering Community (15% marks)
- Style, Comments and Complexity: 20%
Testing
Please note that testing an API implementation is
very important and crucial part of
designing and implementing an API.
We offer the following testing interfaces (for all the APIs you need to implement)
for you to get started,
however note that they only test basic cases. Importantly,
- you need to add more advanced test cases and properly test your API implementations,
- the auto-marking program will use more advanced test cases that are not
included in the test cases provided to you.
Instructions on how to test your API implementations are available on the following page:
Submission
You need to submit the following five files:
- Dijkstra.c
- CentralityMeasures.c
- LanceWilliamsHAC.c
You can now submit the above three files, go to: Assignment-2 Submission page, click the tab named "Make Submission"
You can also submit at the command-line, by running
give cs2521 assign2
As mentioned earlier, please note that,
- all the requried code for each part must be in the respective *.c file.
- you may implement addition helper functions in your files, please declare them as "static" functions.
- after implementing Dijkstra.h, you can use this ADT for the other tasks in the assignment.
However, please note that for our testing, we will use/supply our implementations of Graph.h, PQ.h and Dijkstra.h.
So your programs MUST NOT use any implementation related information that is not available in the respective
header files (*.h files). In other words, you can only use information available in the corresponding *.h files.
- your program must not have any "main" function in any of the submitted files.
- do not submit any other files. For example, you do not need to submit your modified test files or *.h files.
- If you have not implemented any part, you need to still submit an empty file with the corresponding file name.
.
Plagiarism
This is an individual assignment. Each student will have to develop their own solution without help from other people. You are not permitted to exchange code or pseudocode. If you have questions about the assignment, ask your tutor. All work submitted for assessment must be entirely your own work. We regard unacknowledged copying of material, in whole or part, as an extremely serious offence. For further information, read the Course Outline.
-- end --
