Week 04 Tutorial
Binary Search Trees and Balanced Trees
  1. (Splay trees)

    1. Show how a Splay tree would be constructed if the following values were inserted into an initially empty tree in the order given:

      5 3 8 7 4

    2. Let \( t \) be your answer to part a, and consider the following sequence of operations:

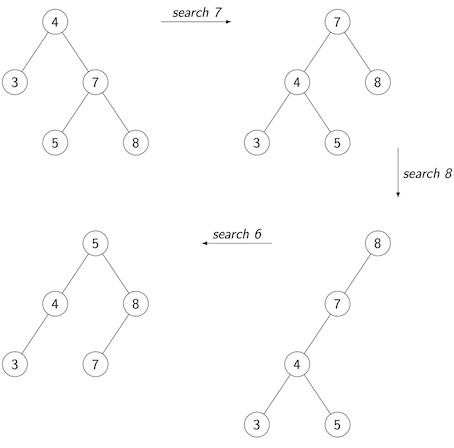
      SearchSplay (t, 7);
SearchSplay (t, 8);
SearchSplay (t, 6);

      Show the tree after each operation.

    1. The following diagram shows how the tree grows based on the pseudocode given in the lecture:

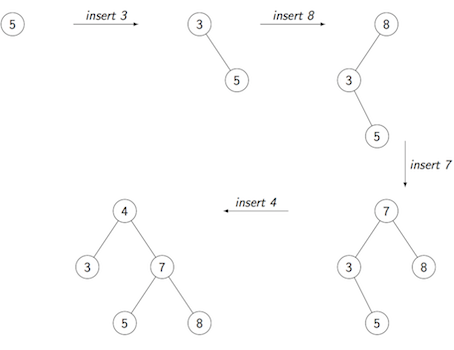
      This is how the tree would grow if root-root rotation were used for the left-left-child and right-right-child cases, as in the standard implementation of Splay trees:

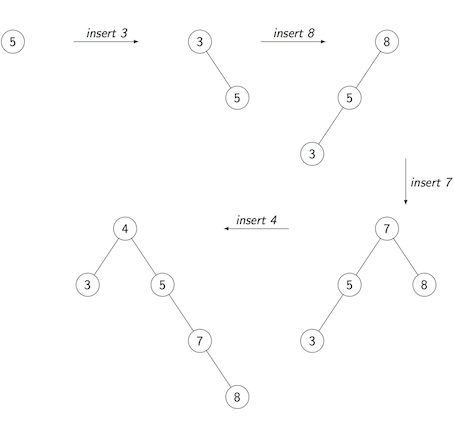
    2. The following diagram shows how the tree changes with each search operation:

  2. (AVL trees)

    Answer the following question without the help of the treeLab program from the lecture.

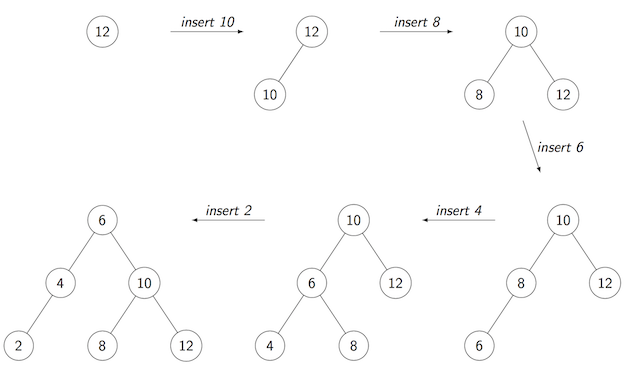
    Show how an AVL tree would be constructed if the following values were inserted into an initially empty tree in the order given:

    12 10 8 6 4 2

    The following diagram shows how the tree grows:

  3. (2-3-4 trees)

    Show how a 2-3-4 tree would be constructed if the following values were inserted into an initially empty tree in the order given:

    1 2 3 4 5 8 6 7 9 10

    Once you have built the tree, count the number of comparisons needed to search for each of the following values in the tree:

    1  7  9  13

    The following diagram shows how the tree grows:

    Search costs (for tree after insertion of 10):

  4. Implement the following function that prints the height difference between the left subtree and the right subtree of every node in a given binary tree, (BSTree t). The function returns the height of a given binary tree. Use the following function interface:

    int printHeightDiff (BSTree t) { ... }